Характеристики случайной дискретной величины Среднее значение величины

Пусть для x возможны значения: x₁, x₂, …, x_k.

Измерения проводятся N раз, результат x_i наблюдается N_i раз, тогда

.

Среднее значение

.

При согласно (1.1) получаем

,

. (1.5)

Среднее значение величины равно сумме произведений ее значений на вероятности этих значений.

При получаем и (1.5) дает нормировку вероятностей

. (1.6)

Свойства среднего

Для и независимых случайных величинx и y выполняются

1. ,

2. ,

3. .

Доказательство 2. Используя (1.5),получаем

;

Доказательство 3.

,

где для независимых случайных величин учтена теорема 2

.

Отклонение от среднего

.

Среднее отклонение от среднего

.

Среднее квадратичное величины

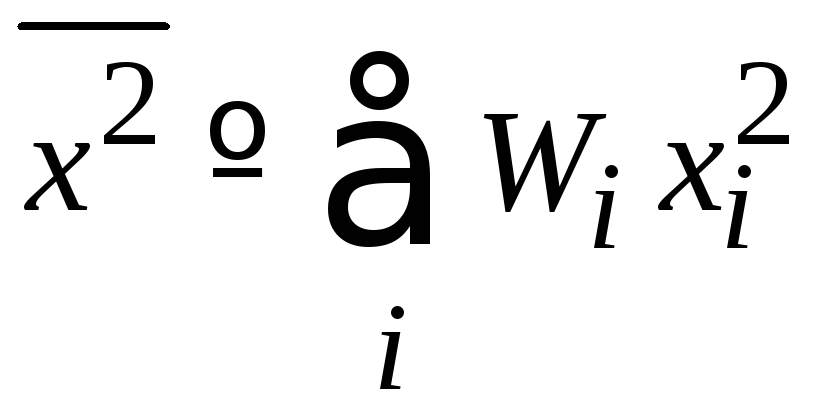. (1.7)

Среднее квадратичное отклонения от среднего – дисперсия

. (1.8)

Флуктуация

. (1.9)

Относительная флуктуация

. (1.10)

Если x случайным образом изменяется с течением времени, то относительная флуктуация показывает долю времени, в течение которой система находится в состоянии с .

Теорема: Относительная флуктуация аддитивной величины, характеризующей систему, уменьшается обратно пропорционально корню квадратному из числа независимых подсистем и мала для макроскопической системы. Примером аддитивной величины (от лат. additivus – прибавляемый) является энергия. Флуктуация энергии для макросистемы ничтожно мала, для микросистемы она существенна.

Доказательство

Аддитивная величина X для системы равна сумме значений x_k для N независимых подсистем

, .

Тогда

,

,

,

где

,

и усреднение произведений характеристик статистически независимых подсистем

, .

Относительная флуктуация

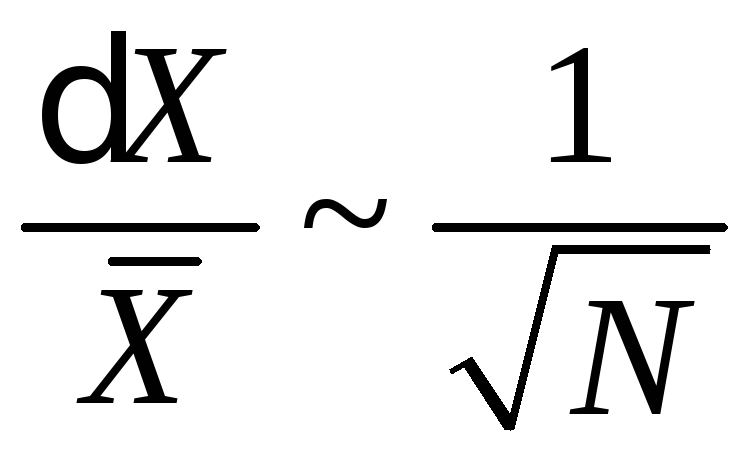. (П.1.2)

Характеристики случайНой непрерывНой величиНы

Плотность вероятности случайной величины x равна вероятности ее обнаружения в единичном интервале около значения x

. (1.11)

Вероятность нахождения в интервале

.

Пример: Пусть – скорость частицы идеального газа. Вероятность обнаружения частицы со скоростью в интервале

,

–концентрация частиц со скоростями в интервале ,

n – концентрация частиц со всевозможными скоростями.

Условие нормировки

. (1.12)

Средние значения

,

. (1.13)

Биномиальное распределение

Описывает N независимых частиц или N независимых случаев.

Если p – вероятность признака у одной частицы, или вероятность одного случая, то вероятность того, что n любых частиц обладают этим признаком, или вероятность одновременного возникновения n случаев:

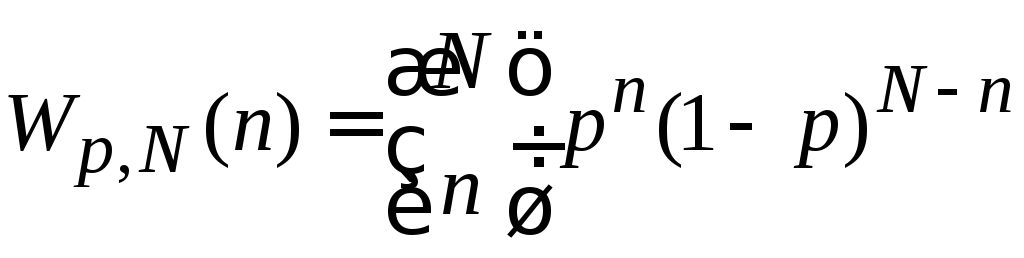, (1.14)

; ;

–биномиальный коэффициент.

Распределение обосновал Якоб Бернулли в 1713 г.

Доказательство:

Объект – идеальный газ из N тождественных частиц в объеме V.

Получим вероятность обнаружения n любых частиц в объеме .

1. Вероятность найти определенную частицу в объеме V согласно определению вероятности (1.4а)

.

Вероятность найти определенную частицу вне объема V

.

Несовместимые события образуют полный набор и удовлетворяют условию нормировки.

2. Вероятность найти n определенных частиц в объеме V согласно теореме об умножении вероятностей независимых событий (1.4б)

.

Вероятность найти (N – n) определенных частиц вне объема V

.

3. Вероятность найти одновременно n определенных частиц в объеме V и (N – n) других частиц вне этого объема

.

4. Взаимная перестановка тождественных частиц дает состояние, не отличимое от исходного. Число таких состояний равно числу сочетаний n частиц из общего числа N, т. е. равно .

5. В результате вероятность найти n любых частиц в объеме V и (N – n) любых других частиц вне V

.