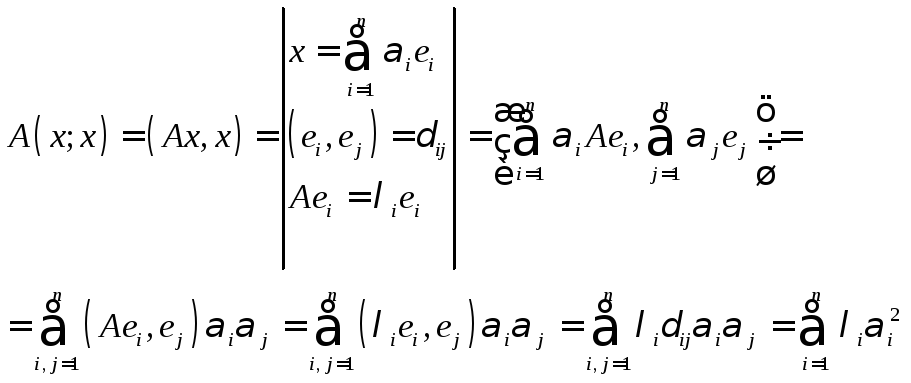- •Линейная алгебра.
- •Определение. Назовем число положительных и число отрицательныхкоэффициентов в каноническом виде квадратичной формы соответственноположительными и отрицательными индексами инерции:.
- •14. Унитарные операторы и их свойства.
- •16. Достаточный признак оператора простой структуры. Доказать, что у всякого линейного оператора в вещественном пространстве существует одномерное (двумерное) инвариантное подпространство.
- •17. Основные свойства симметричных операторов.
- •18. Ортогональные операторы и их свойства.
- •22. Расстояние от точки до плоскости. Расстояние между параллельными плоскостями.
- •23. Приведение уравнения кривой второго порядка к каноническому виду с классификацией возможных типов типов в случае δ≠0
- •30. Выбор базиса в корневом подпространстве. Расщепление корневого подпространства на прямую сумму циклических подпространств.
- •31. Теорема о жордановой нормальной форме линейного оператора и основные этапы ее доказательства.
- •32. Λ – матрицы. Элементарные преобразования λ – матриц. Доказать, что всякую λ – матрицу путем элементарных преобразований можно привести к нормальной диагональной форме.
- •33. Доказать, что нормальная диагональная форма λ – матрицы определяется однозначно.
- •34-36. Вычисление функции от матрицы.
16. Достаточный признак оператора простой структуры. Доказать, что у всякого линейного оператора в вещественном пространстве существует одномерное (двумерное) инвариантное подпространство.
Теорема. Достаточный признак оператора простой структуры. Если все корни характеристического уравнения различны, то линейный оператор А имеет простую структуру.
Доказательство.
Пусть![]() .
Покажем, что система
.
Покажем, что система![]() линейно независима:
линейно независима:![]() (1).
Подействует линейным оператором
(1).
Подействует линейным оператором![]() :
:![]() (2).
Подействует на (2)
линейным оператором
(2).
Подействует на (2)
линейным оператором![]() :
:![]() (3).
Продолжая процесс вплоть до оператора
(3).
Продолжая процесс вплоть до оператора
![]() получим
получим![]() (4).
Заметим, что (4)
– это результат приложения оператора
(4).
Заметим, что (4)
– это результат приложения оператора
![]() к исходному уравнению. Из(4)
следует
к исходному уравнению. Из(4)
следует![]() .
Если к исходному уравнению применить
оператор
.
Если к исходному уравнению применить
оператор![]() можно показать, что
можно показать, что![]() .
И вообще соответствующим выбором
оператора можно добиться, что все
.
И вообще соответствующим выбором
оператора можно добиться, что все![]() .
Следовательно,
.
Следовательно,![]() -
линейно независимы, а А – оператор
простой структуры.
-
линейно независимы, а А – оператор
простой структуры.
Теорема 1. У всякого линейного оператора в вещественном пространстве существует одномерное (двумерное) инвариантное подпространство.
Доказательство.
Выберем в линейном пространстве Х
базис![]() .
В этом базисе линейному оператору А
соответствует матрица
.
В этом базисе линейному оператору А
соответствует матрица![]() ,
преобразующая координаты
,
преобразующая координаты![]() в координаты
в координаты![]() .
Рассмотрим условие
.
Рассмотрим условие![]() в координатной форме:
в координатной форме:
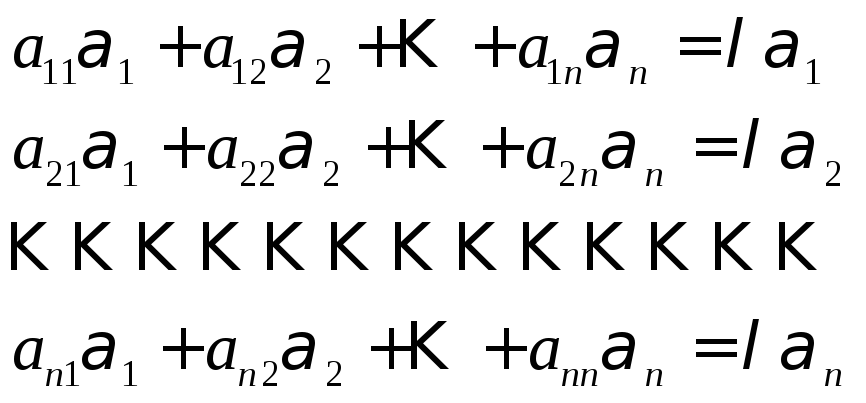 (1)
(1)
Тогда
ненулевое решение (1)
существует, если
![]() (2).
И пусть
(2).
И пусть
![]() - корень уравнения(2).
Возможны два случая:
- корень уравнения(2).
Возможны два случая:
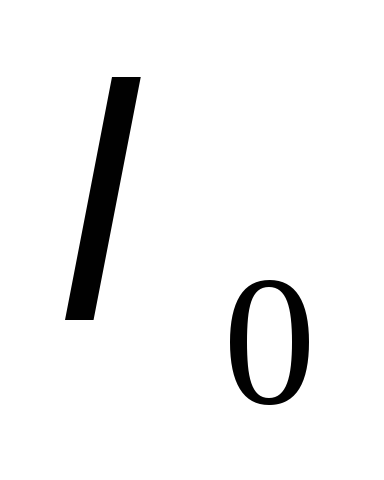 -
вещественное, тогда существует
-
вещественное, тогда существует
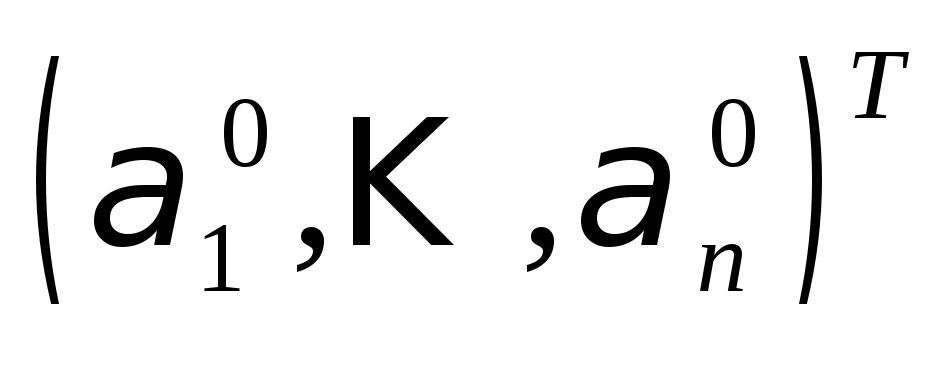 решение системы(1),
определяющее координаты собственного
вектора х. х порождает одномерное
инвариантное пространство;
решение системы(1),
определяющее координаты собственного
вектора х. х порождает одномерное
инвариантное пространство;
![]() -
комплексное (
-
комплексное (![]() ).
Пусть
).
Пусть![]() - это решение системы(1).
Подставим эти числа в (1)
и отделим вещественную часть от мнимой.
- это решение системы(1).
Подставим эти числа в (1)
и отделим вещественную часть от мнимой.
![]() (3).
Будем
считать
(3).
Будем
считать
![]() - координатами некоторого вектора х, а
- координатами некоторого вектора х, а![]() - координатами у, тогда
- координатами у, тогда![]() (4).
Равенство (4)
означает, что линейная оболочка
(4).
Равенство (4)
означает, что линейная оболочка
![]() есть двумерное инвариантное подпространство
относительное оператора.
есть двумерное инвариантное подпространство
относительное оператора.
17. Основные свойства симметричных операторов.
Определение.
Самосопряженный
оператор в евклидовом пространстве
называется симметричным,
если![]() .
.
Утверждение.
Пусть
![]() - ортонормированный базис,
- ортонормированный базис,![]() .
Пусть х и у в базисе е имеют координаты:
.
Пусть х и у в базисе е имеют координаты:![]() .
Тогда
.
Тогда![]() .
Это утверждение верно только в
ортонормированном базисе.
.
Это утверждение верно только в
ортонормированном базисе.
Лемма 1. Для всякого симметричного оператора существует одномерное инвариантное пространство.
Доказательство.
Из теоремы
1 (билет 16) следует, что нам нужно доказать
существование вещественного корня
![]() характеристического уравнения
характеристического уравнения![]() (2).
Предположим, что
(2).
Предположим, что![]() .
Построим два вектор х и у такие, что
.
Построим два вектор х и у такие, что![]() .
.
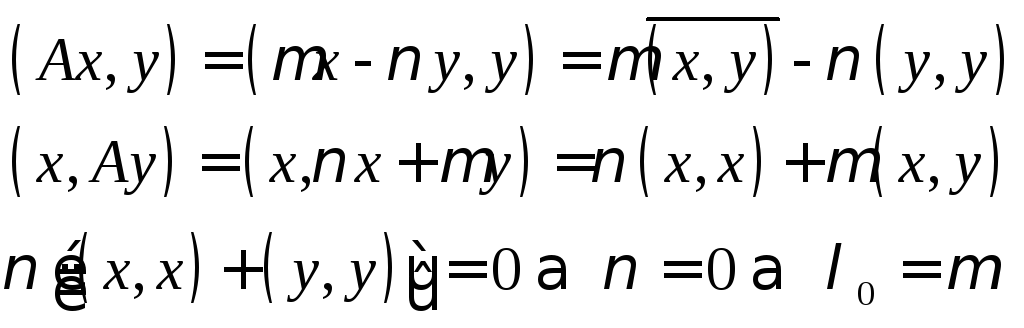
Лемма
2. Пусть А –
симметричный оператор, а е – его
собственный вектор, тогда множество
векторов, ортогональных е, образуют
(n-1)-мерное
инвариантное пространство:![]() .
.
Доказательство.
Пусть![]() .
.
Теорема 2. Существует ортонормированный базис, в котором матрица симметричного оператора А диагональна.
Доказательство.
По лемме 1 линейный оператор А имеет
хотя бы один собственный вектор, т.к.
![]() -
инвариантное относительно линейного
оператора А пространство, то в
-
инвариантное относительно линейного
оператора А пространство, то в![]() существует собственный вектор
существует собственный вектор![]() …
В итоге мы получимn
собственных векторов, ортогональных
по построению. Затем пронормируем их.
…
В итоге мы получимn
собственных векторов, ортогональных
по построению. Затем пронормируем их.
Теорема
3. Пусть
![]() - квадратичная форма вn-мерном
евклидовом пространстве, тогда существует
ортонормированный базис
- квадратичная форма вn-мерном
евклидовом пространстве, тогда существует
ортонормированный базис![]() ,
в котором эта квадратичная форма имеет
вид:
,
в котором эта квадратичная форма имеет
вид:![]() ,
где
,
где![]() - собственные значения симметричного
оператора.
- собственные значения симметричного
оператора.
Доказательство.![]() .
Выберем ортонормированный базис е из
собственных векторов (существует по
теореме 2).
.
Выберем ортонормированный базис е из
собственных векторов (существует по
теореме 2).