
- •Линейная алгебра.
- •Определение. Назовем число положительных и число отрицательныхкоэффициентов в каноническом виде квадратичной формы соответственноположительными и отрицательными индексами инерции:.
- •14. Унитарные операторы и их свойства.
- •16. Достаточный признак оператора простой структуры. Доказать, что у всякого линейного оператора в вещественном пространстве существует одномерное (двумерное) инвариантное подпространство.
- •17. Основные свойства симметричных операторов.
- •18. Ортогональные операторы и их свойства.
- •22. Расстояние от точки до плоскости. Расстояние между параллельными плоскостями.
- •23. Приведение уравнения кривой второго порядка к каноническому виду с классификацией возможных типов типов в случае δ≠0
- •30. Выбор базиса в корневом подпространстве. Расщепление корневого подпространства на прямую сумму циклических подпространств.
- •31. Теорема о жордановой нормальной форме линейного оператора и основные этапы ее доказательства.
- •32. Λ – матрицы. Элементарные преобразования λ – матриц. Доказать, что всякую λ – матрицу путем элементарных преобразований можно привести к нормальной диагональной форме.
- •33. Доказать, что нормальная диагональная форма λ – матрицы определяется однозначно.
- •34-36. Вычисление функции от матрицы.
33. Доказать, что нормальная диагональная форма λ – матрицы определяется однозначно.
Теорема: Нормальная диагональная форма данной λ-матрицы A(λ) определяется по ней однозначно. Если Dk(λ) (k=2,3,…,r) – наибольший общий делитель миноров k-го порядка матрицы A(λ), а Dr+1(λ) = … = Dn(λ) = 0, то элементы нормальной диагональной формы определяются по формулам
Ek(λ)
=
![]() (k=1,2,…,r)
(k=1,2,…,r)
Er+1(λ) = Er+2(λ) = … = En(λ) = 0
Доказательство: Мы показали, что при элементарных преобразованиях многочлены Dk(λ) не меняются. Поэтому, если матрица A(λ) эквивалентна диагональной нормальной матрице, то Dk(λ) у них совпадают. Так как для матрицы мы получили, что Dk(λ) = E1(λ)…Ek(λ) (k=1,2,…,r ; r<=n) и что Dr+1(λ) = Dr+2(λ) = … = Dn(λ) = 0, то теорема доказана
34-36. Вычисление функции от матрицы.
Определение.
Пусть даны квадратичная матрица А
размерностью
![]() и функция
и функция![]() скалярного аргумента
скалярного аргумента![]() .
Распространим
.
Распространим![]() на матричное значение аргумента. Если
на матричное значение аргумента. Если![]() ,
тофункция
от матрицы приобретает
вид
,
тофункция
от матрицы приобретает
вид![]() .
.
Теорема
Гамильтона. Пусть
![]() - минимальный многочлен. Разложим его
на множители
- минимальный многочлен. Разложим его
на множители![]() (1),
где
(1),
где
![]() - все различные собственные значения
матрицы А. Степень же
- все различные собственные значения
матрицы А. Степень же![]()
![]() чисел
чисел![]() (2)
будем называть значениями
функции
(2)
будем называть значениями
функции
![]() на спектре матрицы А. Очевидно, чтобы
значения функции
на спектре матрицы А. Очевидно, чтобы
значения функции![]() на спектре матрицы А полностью определяют
на спектре матрицы А полностью определяют![]() ,
т.е. все функции
,
т.е. все функции![]() ,
имеющие одни и те же значения на спектре
матрицы А имели одно и то же матричное
значение
,
имеющие одни и те же значения на спектре
матрицы А имели одно и то же матричное
значение![]() .
Т.о. для определения
.
Т.о. для определения![]() в общем случае достаточно найти
многочлен
в общем случае достаточно найти
многочлен![]() ,
который принимал бы те же значения на
спектре матрицы А, что и
,
который принимал бы те же значения на
спектре матрицы А, что и![]() ,
и положить, что
,
и положить, что![]() .
.
Определение.
Если функция
![]() определена на спектре матрицы А, то
определена на спектре матрицы А, то![]() ,
где
,
где![]() - любой многочлен, принимающий на спектре
те же значения, что и
- любой многочлен, принимающий на спектре
те же значения, что и![]() ,
т.е.
,
т.е.![]() .Среди
всех многочленов с комплексными
коэффициентами, принимающих те же
значения на спектре, что и
.Среди
всех многочленов с комплексными
коэффициентами, принимающих те же
значения на спектре, что и![]() ,
существует единственный многочлен
,
существует единственный многочлен![]() ,
степень которого меньшеm.
Этот многочлен однозначно определяется
интерполирующими условиями:
,
степень которого меньшеm.
Этот многочлен однозначно определяется
интерполирующими условиями:
![]() (3)
– интерполяционный
многочлен Лагранжа-Сильвестра.
(3)
– интерполяционный
многочлен Лагранжа-Сильвестра.
Определение.
Пусть функция![]() ,
определена на спектре матрицы А, а
,
определена на спектре матрицы А, а![]() - соответствующий интерполяционный
многочлен. Тогда
- соответствующий интерполяционный
многочлен. Тогда![]() .
.
Замечание.
Получили, что если
![]() матрицы А не имеет кратных корней
(матрица простой структуры) и в равенстве(1)
матрицы А не имеет кратных корней
(матрица простой структуры) и в равенстве(1)![]() ,
то для того, чтобы
,
то для того, чтобы
![]() имело смысл достаточно, чтобы
имело смысл достаточно, чтобы![]() была определена в точках
была определена в точках![]() ,
если же все
,
если же все![]() имеют кратные корни, то в некоторых
точках соотношения(2)
должны быть определены и производные
до известного порядка.
имеют кратные корни, то в некоторых
точках соотношения(2)
должны быть определены и производные
до известного порядка.
Свойства функций от матриц:
Если
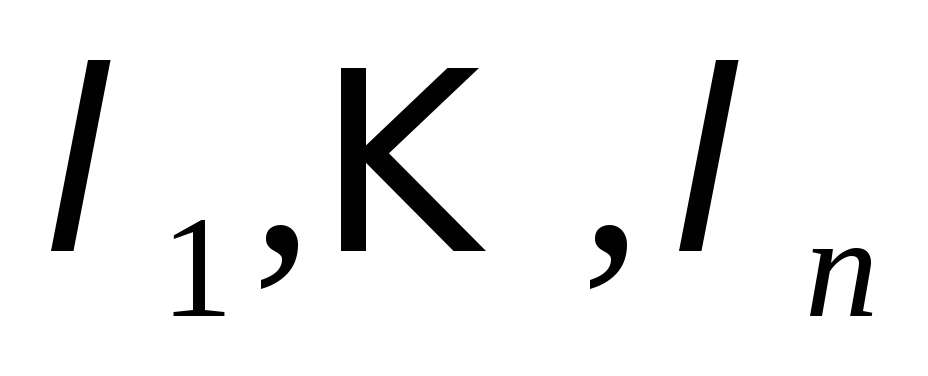 - собственные числа матрицы Аn-ого
порядка, то
- собственные числа матрицы Аn-ого
порядка, то
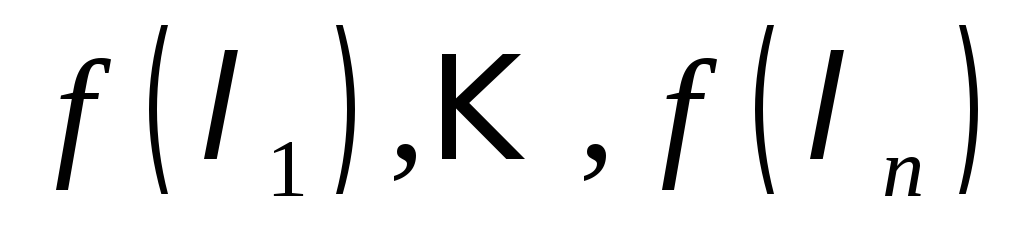 - собственные числа матрицы
- собственные числа матрицы .
.Если матрицы А и В подобны, т.е.
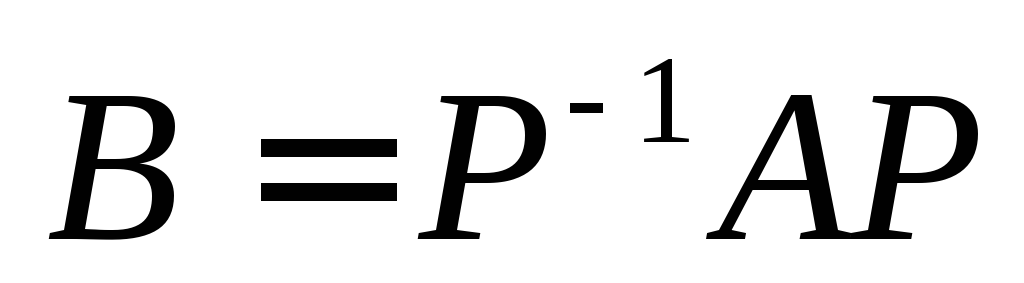 ,
то матрицы
,
то матрицы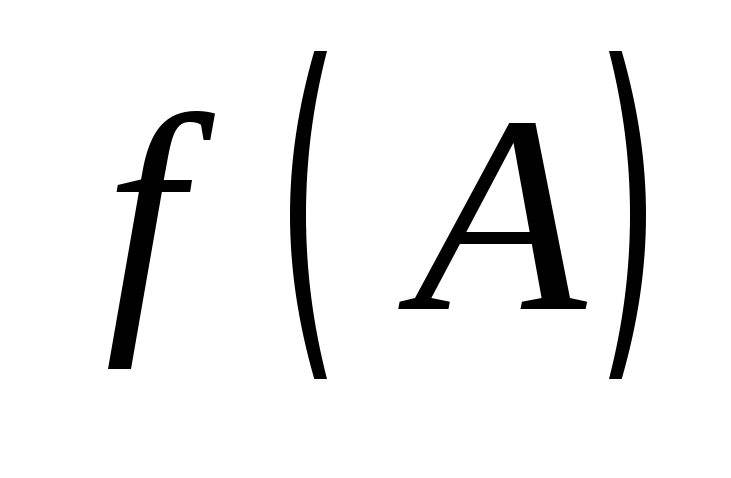 и
и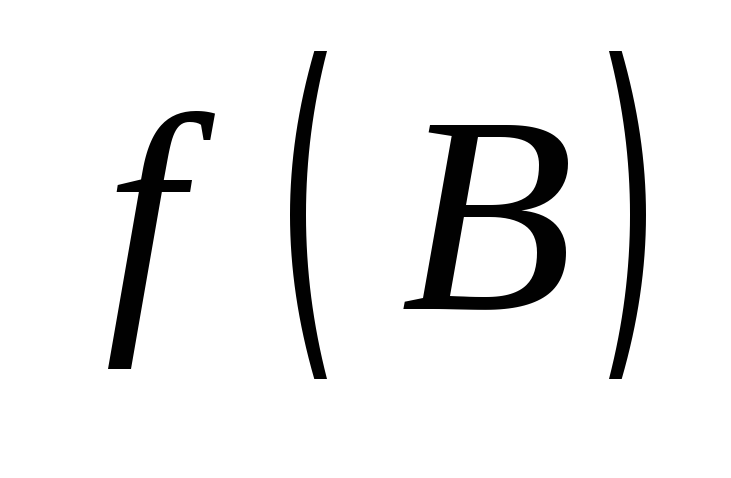 также подобны, причем
также подобны, причем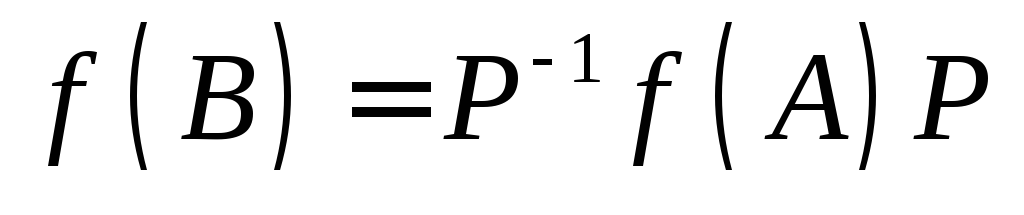 .Доказательство.
Пусть
.Доказательство.
Пусть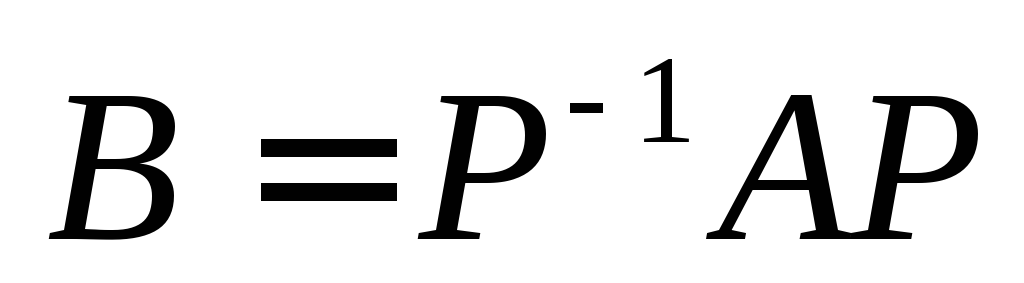 .
Покажем, что
.
Покажем, что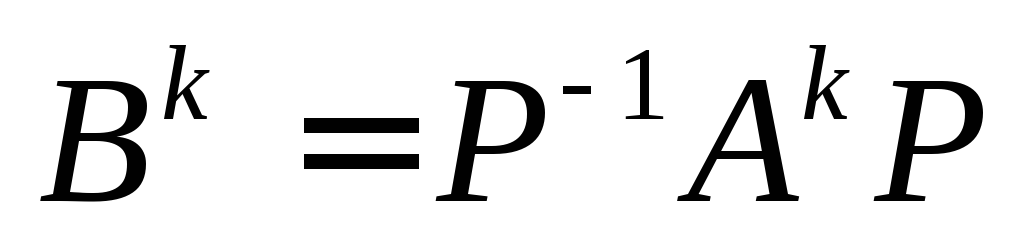 ,
используя метод математической индукции.
Дляk=1,
это очевидно. Пусть это верно и для k=m.
Докажем, что это верно и для k=m+1.
Действительно,
,
используя метод математической индукции.
Дляk=1,
это очевидно. Пусть это верно и для k=m.
Докажем, что это верно и для k=m+1.
Действительно, .
Тогда
.
Тогда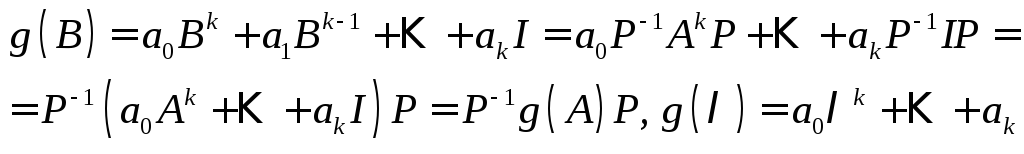 .
.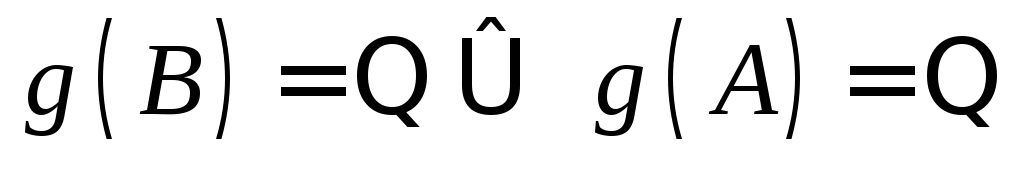 .
Т.о.
две подобные матрицы имеют одинаковые
минимальные многочлены и аналогично
.
Т.о.
две подобные матрицы имеют одинаковые
минимальные многочлены и аналогично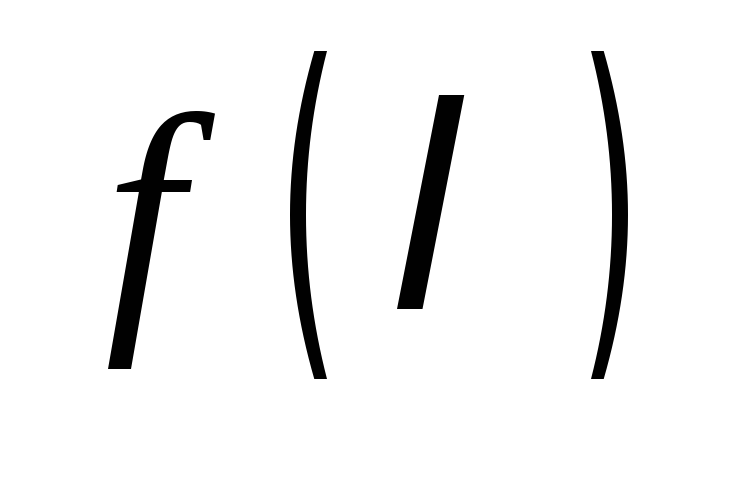 принимает одни и те же значение как на
спектре матрицы А так и на спектре
матрицы В. Поэтому существует
интерполяционный многочлен
принимает одни и те же значение как на
спектре матрицы А так и на спектре
матрицы В. Поэтому существует
интерполяционный многочлен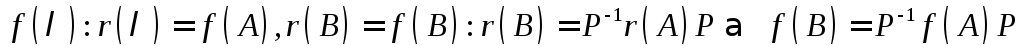 .
.Пусть А – квазидиагональная матрица
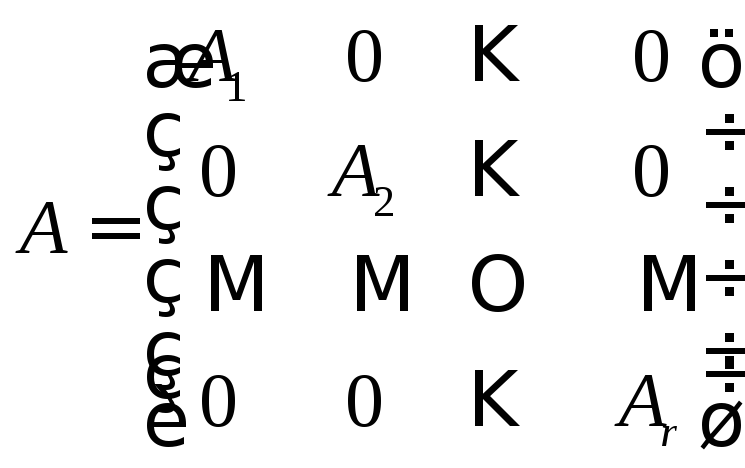 ,
тогда
,
тогда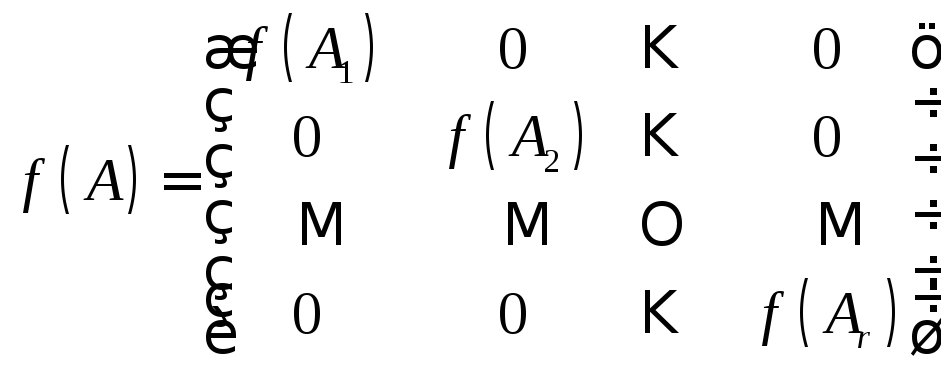 .Доказательство.
Обозначим через
.Доказательство.
Обозначим через
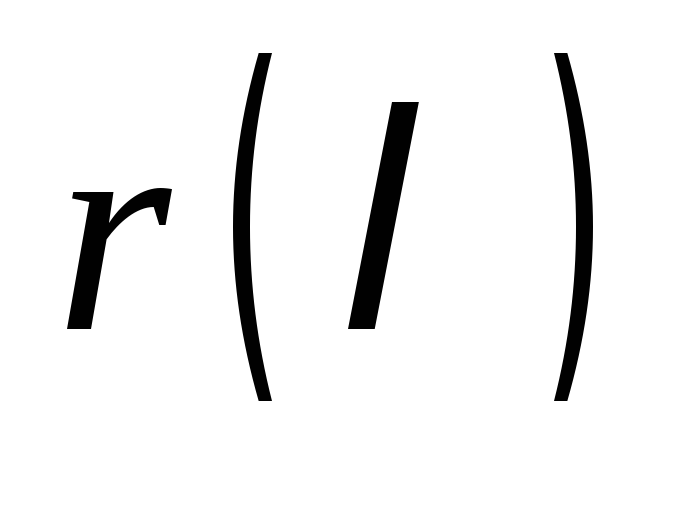 интерполяционный многочлен функции
интерполяционный многочлен функции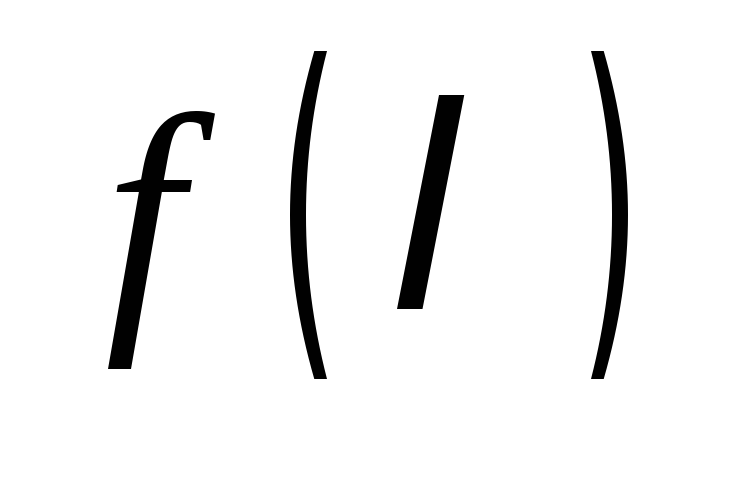 на спектре матрицы А.
на спектре матрицы А.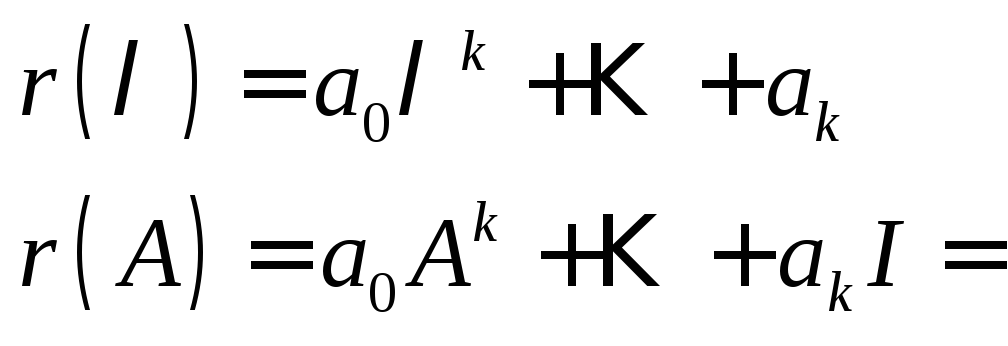
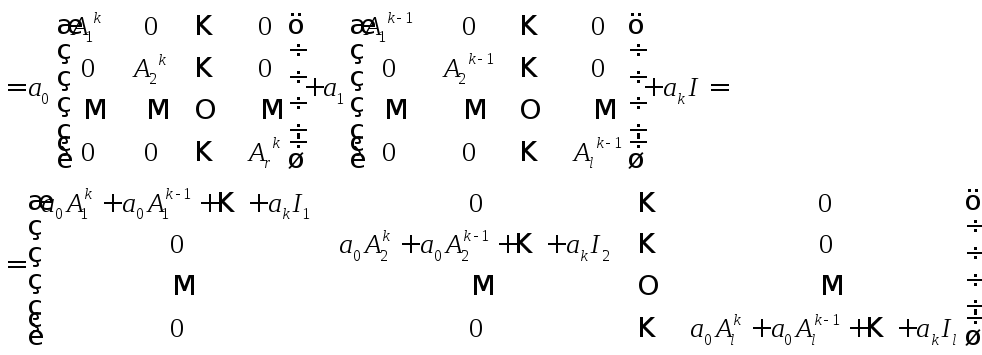 (5)
(5)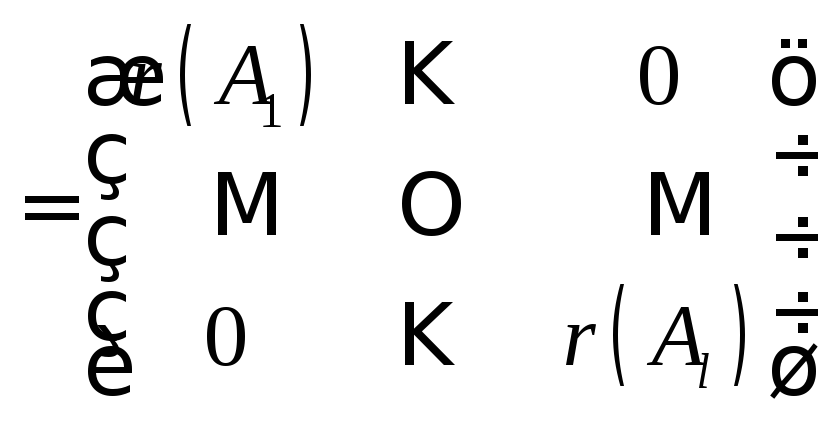 .
Минимальный многочлен
.
Минимальный многочлен
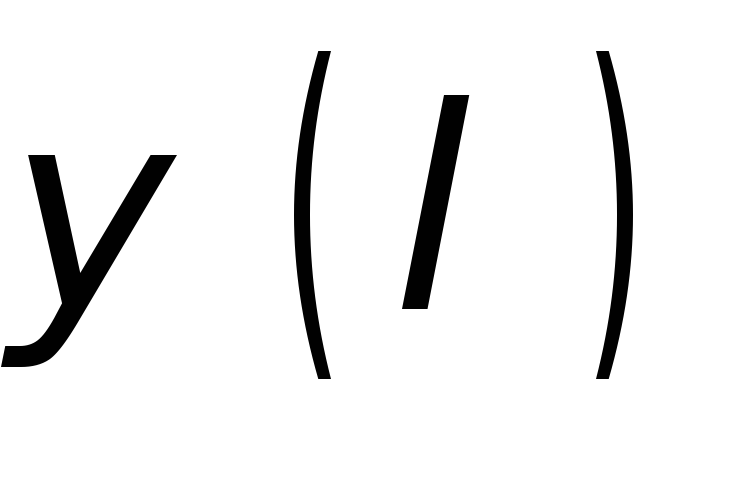 является аннулирующим многочленом для
матрицы
является аннулирующим многочленом для
матрицы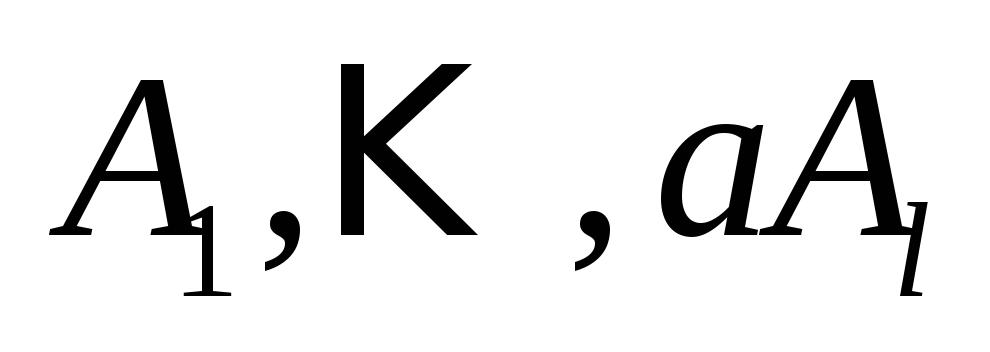 ,
поэтому из равенства
,
поэтому из равенства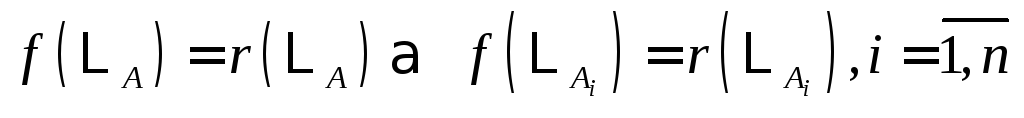 .
Поэтому
.
Поэтому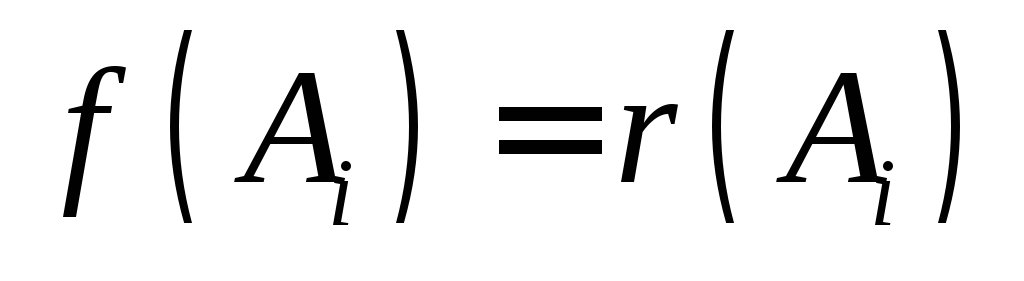 и
и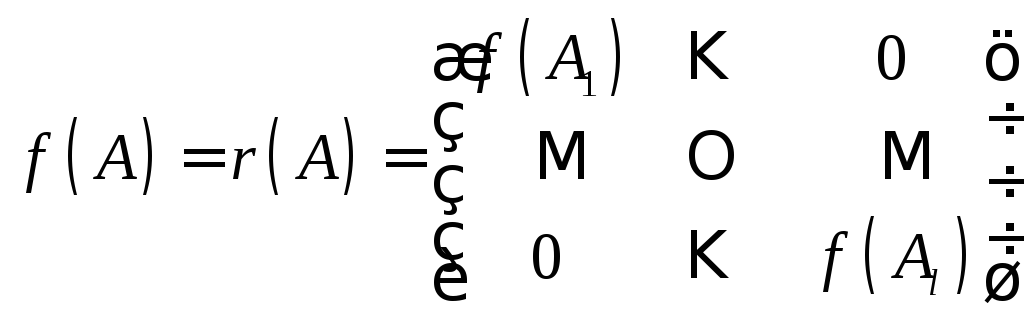 .
.
Интерполяционный
многочлен Лагранжа-Сильвестра.
Пусть
![]() - минимальный многочлен матрицы А,
- минимальный многочлен матрицы А,![]() .
.![]() -
степень
-
степень![]() .
Представим
.
Представим![]() является правильной дробью в виде суммы
дробей:
является правильной дробью в виде суммы
дробей:![]() (6),
где
(6),
где
![]() - некоторые числа. Для определения
числителя простой дроби умножим обе
части(6)
на
- некоторые числа. Для определения
числителя простой дроби умножим обе
части(6)
на
![]() (7),
где
(7),
где
![]() - рациональная функция, не обращающаяся
в бесконечность при
- рациональная функция, не обращающаяся
в бесконечность при![]() .
Обозначим через
.
Обозначим через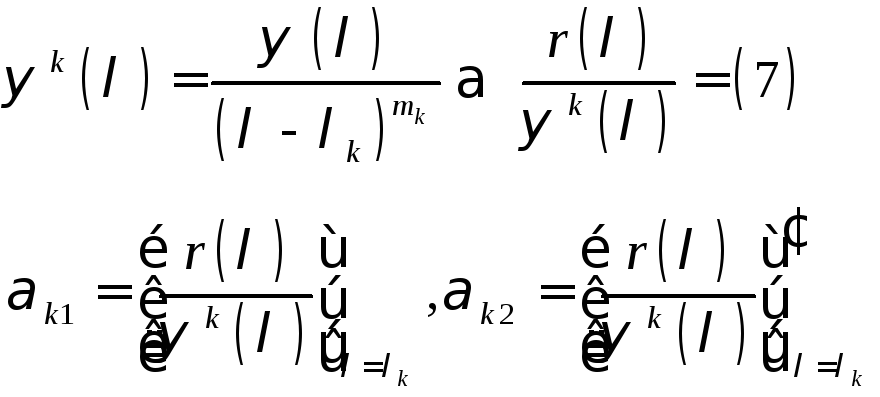 .
.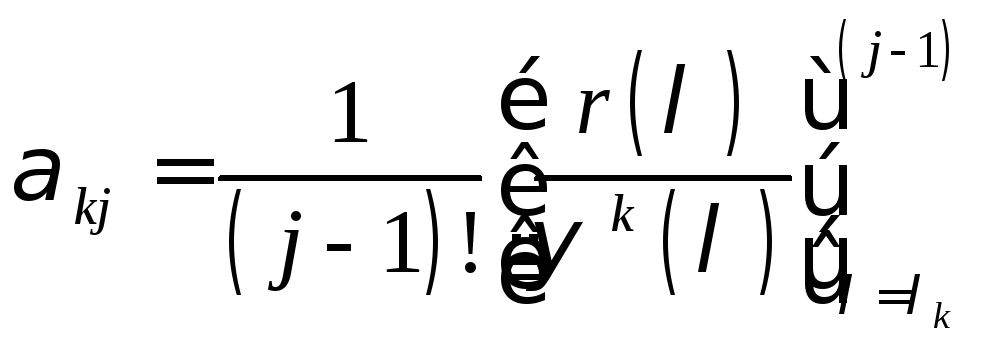 (8)
(8)
Формулы
(8)
показывают, что числители
![]() в правой части(6)
выражаются через значения многочлена
в правой части(6)
выражаются через значения многочлена
![]() на спектре матрицы А, а эти значения нам
известны. А именно, они равны соответственным
значения функции
на спектре матрицы А, а эти значения нам
известны. А именно, они равны соответственным
значения функции![]() и ее производной:
и ее производной: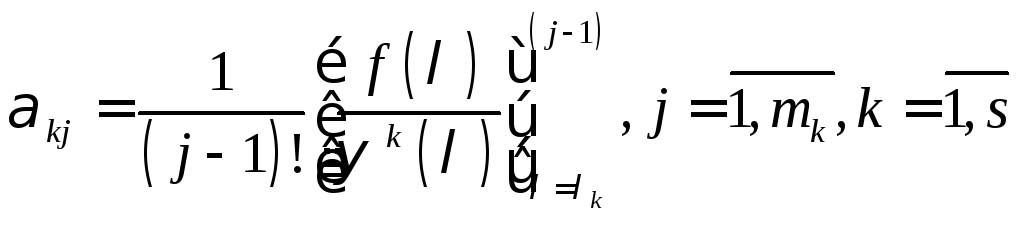 (9’).
После того, как все
(9’).
После того, как все![]() найдены, мы определим
найдены, мы определим![]() по следующей формуле, которая получается
умножением обеих частей равенства(6)
на
по следующей формуле, которая получается
умножением обеих частей равенства(6)
на![]() :
:![]() (10).
Заметим, что в соотношении
(10) выражение
в квадратных скобках в силу (9’)
равно сумме первых
(10).
Заметим, что в соотношении
(10) выражение
в квадратных скобках в силу (9’)
равно сумме первых
![]() членов разложения Тейлора по степеням
членов разложения Тейлора по степеням![]() для
для![]() .
.
Основная
формула.
Вернемся к (10).
Подставив в нее (9’)
для коэффициентов
![]() и объединив члены, содержащие одно и
тоже значение
и объединив члены, содержащие одно и
тоже значение![]() и какой-либо ее производной, представим
и какой-либо ее производной, представим![]() в виде
в виде![]() (11),
где
(11),
где
![]() - полином
- полином![]() степени меньшей степени
степени меньшей степени![]() .
Эти полиномы определяются заданием
.
Эти полиномы определяются заданием![]() и не зависит от выбора функции
и не зависит от выбора функции![]() .
Число этих полиномов равно числу значений
.
Число этих полиномов равно числу значений![]() на спектре матрицы А и равноm,
где m
– степень минимального многочлена. Из
формулы (10)
следует основная формула для нахождения
функции от матрицы, а именно:
на спектре матрицы А и равноm,
где m
– степень минимального многочлена. Из
формулы (10)
следует основная формула для нахождения
функции от матрицы, а именно:
![]() (12),
матрицы
(12),
матрицы
![]() являются компонентами матрицы А. Они
вполне определяются заданием матрицы
А и не зависят от выбора функции
являются компонентами матрицы А. Они
вполне определяются заданием матрицы
А и не зависят от выбора функции![]() .
В правой части формулы(12),
функция
.
В правой части формулы(12),
функция
![]() представлена только своими значениями
на спектре матрицы А.
представлена только своими значениями
на спектре матрицы А.
