1.1.3. Некоторые из основных приемов работы в MatLab

В MatLab используются все буквы латинского алфавита и арабские цифры от 0 до 9. Как и в С++, большие и малые буквы различаются. Кроме букв латинского алфавита используются все специальные символы клавиатуры компьютера. Все символы после символа ‘%’ до конца текущей строки в MatLab рассматриваются как комментарии.

Выполнение арифметических вычислений. Используются символы: `+`, `-`, `*`, `/` и `^` (возведение в степень). Для установления приоритета выполнения действий следует использовать круглые скобки `()`, а для подавления печати результата вычислений необходимо применять символ `;`. Пусть необходимо вычислить следующее выражение .

Щёлкнем ЛКМ в командной строке (там после этого должен появиться мигающий курсор) и наберем следующую последовательность символов 2^3.2/4.7-4*5.6 и нажмите на клавишу <<Enter>>. В рабочем окне появится запись

>> 2^3.2/4.7-4*5.6

ans =

-20.4448

>>

− к конце которой будет расположен мигающий курсор.

Если набрать следующую последовательность символов 2^3.2/4.7-4*5.6; и тоже нажать на клавишу <<Enter>>, то в рабочем окне появится другая запись

>> 2^3.2/4.7-4*5.6;

>>

− с мигающим курсором в конце. Печать результата вычислений здесь подавлена символом `;`. Он хранится в переменной с именем ans и для его получения следует в командной строке набрать ans<<Enter>>. Кроме того в дальнейших вычислениях имя этой переменной (ans) можно подставлять вместо результата вычислений.

Если имеется необходимость повторно вызвать ранее уже введённую запись, то это легче всего сделать, используя клавиши <<>> и <<>>.

Вообще говоря, имя переменной может состоять из букв латинского алфавита, знака подчёркивания и цифр, и обязательно должно начинаться с буквы. Для того чтобы проверить занято ли уже какое-либо имя следует набрать в командной строке exist(‘имя переменной’). Нулевой ответ при выполнении этой команды (вызова функции exist) говорит, что имя свободно. Пример.

>> exist('a6')

ans =

0

Для изменения формата выводимых числовых данных можно поступить двумя способами. Первый состоит в вызове в командной строке функции format с одним из её аргументов: short, short e, long, long e, bank, compact, loose. Пример

>> format short

Второй способ состоит в вызове (ЛКМ через меню File Preferences…) окна Preferences, которое представлено на рис. 1.2. Здесь в ниспадающем списке элемента Numeric format: и следует выбрать желаемый числовой формат для выводимых данных. Помимо этого там же ниже в элементе Numeric display: можно изменить и вид выводимой в командном окне информации (компактный − compact или свободный − loose). Завершить выбор следует щелчком ЛКМ по кнопке OK.

Рис. 1.2. Окно Preferences

Массивы и работа с ними. Все данные MatLab представляет в виде массивов. Простое число в MatLab представляется в виде двумерного массива размером один на один. Массив − это упорядоченная, пронумерованная совокупность однородных данных, имеющая имя. Массивы бывают одномерными (вектор-столбцы и вектор-строки), двумерные и многомерные. В MatLab нумерация элементов массивов начинается с единицы.

Ввод вектор-строки осуществляется в квадратных скобках. При этом элементы следует отделять друг от друга пробелом или запятой. Пример

>> a=[0.8 2.3 9.1]

a =

8.0000e-001 2.3000e+000 9.1000e+000

Ввод вектор-столбца также осуществляется в квадратных скобках, но при этом элементы отделяются друг от друга точкой с запятой. Пример

>> b=[-2.2;5.9;0.7]

b =

-2.2000e+000

5.9000e+000

7.0000e-001

Над векторами определены следующие операции: вычисления его длины, транспонирования, сложения, вычитания, умножения на число, скалярное и векторное (только для трёхэлементных векторов) произведения, как показано ниже

>> L=length(a) % вычисление длины вектора

L =

3

>> ar=a' % транспонирование вектора

ar =

0.8000

2.3000

9.1000

>> c=[0.2 0.7 0.9];

>> d=a+c % вычисление суммы векторов

d =

1 3 10

>> g=a-c % вычисление разности векторов

g =

0.6000 1.6000 8.2000

>> z=a*2 % умножение вектора на число

z =

1.6000 4.6000 18.2000

>> u=dot(a,c) % скалярное умножение векторов

u =

9.9600

>> y=cross(a,c) % векторное умножение векторов

y =

-4.3000 1.1000 0.1000

Векторы могут быть элементами при определении новых векторов, например

>> ac=[a,c]

ac =

0.8000 2.3000 9.1000 0.2000 0.7000 0.9000

>> act=[ar;c']

act =

0.8000

2.3000

9.1000

0.2000

0.7000

0.9000

Для доступа к элементу массива следует после имени массива в круглых скобках указать его индекс, например

>> act(3)+y(1)

ans =

4.8000

При работе с индексами удобна индексация при помощи символа ‘:’. Примеры

>> act(2:5)=0

act =

0.8000

0

0

0

0

0.9000

>> x=0:2*pi/9:2*pi % начальное значение 0, шаг − , конечное −

x =

Columns 1 through 9

0 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888 4.8869 5.5851

Column 10

6.2832

Над векторами возможны так называемые поэлементные операции (поэлементные умножение, деление и возведение в степень), как показано ниже

>> v=a.*c % поэлементное умножение

v =

0.1600 1.6100 8.1900

>> z=a./c % поэлементное деление

z =

4.0000 3.2857 10.1111

>> s=a.^c % поэлементное возведение в степень

s =

0.9564 1.7915 7.2969

В системе MatLab не определены поэлементное сложение и вычитание.

Ввод двумерных массивов (прямоугольных матриц) осуществляется по строкам. Пусть, например, необходимо ввести матрицу

.

Это можно сделать тремя способами:

>> A=[0.4 -4.5 8.3;6.8 0.9 1.1; -6.3 3.5 4.7] % отделяем строки символом ‘;’

A =

0.4000 -4.5000 8.3000

6.8000 0.9000 1.1000

-6.3000 3.5000 4.7000

B=[ 1.3 5.2 -8.1<<Enter>> % отделяем строки нажатием

-1.7 2.4 0.3<<Enter>> % на клавишу <<Enter>>

6.6 -7.1 1.0]<<Enter>>

B =

1.3000 5.2000 -8.1000

-1.7000 2.4000 0.3000

6.6000 -7.1000 1.0000

>> D=[[3;4] [-1;3] [6;0]] % элементами строки являются столбцы

D =

3 -1 6

4 3 0

Над матрицами определены следующие операции: вычисление размера матрицы, вычисление числа элементов матрицы, транспонирование, сложение и вычитание матриц (как для векторов), умножение на число (также как и для векторов), а также матричное произведение и возведение в степень (для квадратных матриц), как показано ниже

>> C=[4.4 0.7 -0.6; 2.8 -0.1 5.6] % ввод матрицы

C =

4.4000 0.7000 -0.6000

2.8000 -0.1000 5.6000

>> s=size(C) % вычисление размера матрицы

s =

2 3

>> C1=C.' % транспонирование матрицы

C1 =

4.4000 2.8000

0.7000 -0.1000

-0.6000 5.6000

>> n=numel(A) % вычисление числа элементов в матрице

n =

9

>> P=A*B % матричное произведение

P =

62.9500 -67.6500 3.7100

14.5700 29.7100 -53.7100

16.8800 -57.7300 56.7800

>> PP=A^2 % возведение в степень

PP =

-82.7300 23.2000 37.3800

1.9100 -25.9400 62.6000

-8.3300 47.9500 -26.3500

Обращение к элементам матрицы выполняется аналогично обращению к элементам вектора, но с использованием запятой, например

>> C(2,2)=-10 % элементу присваивается значение

C =

4.4000 0.7000 -0.6000

2.8000 -10.0000 5.6000

>> c121=C(1:2,1) % выделяются элементы С(1,1) и С(2,1)

c121 =

4.4000

2.8000

>> PP(:,2)=[] % удаляется второй столбец

PP =

-82.7300 37.3800

1.9100 62.6000

-8.3300 -26.3500

>> PP(:,3)=[1 2 3] % добавляется третий столбец

PP =

-82.7300 37.3800 1.0000

1.9100 62.6000 2.0000

-8.3300 -26.3500 3.0000

Для матриц, как и для векторов, определены следующие поэлементные операции:

A.*B − поэлементные умножения;

A./B − поэлементные деления;

A.^p − поэлементное возведение в степень (p − число);

A.^B − возведение элементов матрицы A в степени, равные соответствующим элементам матрицы B.

Элементарные функции системы MatLab. MatLab включает в себя огромный набор функций. Для знакомства с ними и выбора необходимой следует воспользоваться справочной службой системы через меню Help Product Help. Откроется окно и в нём в навигационном дереве, расположенном слева, следует выбрать пункт MATLAB, как показано на рис. 1.3. При использовании функций не следует забывать, что в MatLab все данные − суть матрицы.

Рис. 1.3. Окно справочной системы

Построение таблицы значений функции пользователя. Пусть необходимо построить таблицу значений функции для значений переменной х от 0.1 и до 2.5 с шагом 0.3. Требуемое выполняется в два этапа.

1. Создаётся вектор-строка х, которая содержит координаты требуемых точек.

2. Для каждого элемента вектора х вычисляется значение функции y(x) и полученное значение записывается в вектор-строку − как показано ниже (операции умножения, деления и возведения в степень в выражении для функции должны выполняться поэлементно!)

>> x=[0.1:0.3:2.5]

x =

0.1000 0.4000 0.7000 1.0000 1.3000 1.6000 1.9000 2.2000 2.5000

>> y=sin(x).^3./(1-0.5*cos(x))+exp(-x).*log10(x)

y =

-0.9029 -0.1573 0.3560 0.8164 1.0638 1.0256 0.7712 0.4463 0.1857

Построение графика функции. Если в следующей строке командного окна вызвать функцию plot(x,y), то откроется окно, показанное на рис. 1.4, с искомым графиком.

Рис. 1.4. Окно графика

Для того, чтобы на одной координатной плоскости построить графики двух функций (например, y(x) и sin(3x)) следует вызвать функцию plot со следующим списком аргументов

>> plot(x,y,x,sin(3*x))

После выполнения сказанного вид окна графика приобретёт вид, представленный на рис. 1.5. Если желательно, чтобы графики кривых не выглядели ломанными, то необходимо при определении вектора х выбрать меньший шаг.

Рис. 1.5. Окно графика

Функция plot позволяет пользователю достаточно гибко управлять процессом визуализации результатов вычислений. Один из возможных её синтаксисов

plot(X1,Y1,LineSpec1,X2,Y2,LineSpec2,...), где Х1, Х2, … − имена векторов оси абсцисс; Y1, Y2, … − имена векторов оси ординат; LineSpec1, LineSpec2, … − спецификации 1-ой, 2-ой и т. д. линий, записываемы в апострофах (см. таблицу 1.1). Пример

>> x1=[0:0.01:2:pi];

>> t3=[-pi:0.05:pi];

>> r1=exp(-x1).*sin(x1);

>> w4=t3.^2.*cos(t3);

>> plot(x1,r1,'r*',t3,w4,'k--')

Записанное выше приведёт к построению графика, показанного на рис. 1.6.

Таблица 1.1

Цвет линии		Тип линии		Тип маркера
y	желтый	-	Сплошная	.	точка
m	розовый	:	Пунктирная	o	кружок
c	голубой	-.	штрих-пунктирная	x	крестик
r	красный	--	Штриховая	+	знак плюс
g	зеленый			*	звездочка
b	синий			s	квадрат
w	белый			d	ромб
k	черный			v	треугольник вершиной вниз
				^	треугольник вершиной вверх
				<	треугольник вершиной влево
				>	треугольник вершиной вправо
				p	пятиконечная звезда
				h	Шестиконечная звезда

>> plotyy(x1,r1,t3,w4)

Рис. 1.6. Окно графика

Из рассмотрения этого рисунка видно, что значения двух функций сильно отличаются по величине и для них желательно иметь несколько отличающиеся оси ординат. Последнее достигается использованием функции (результат − на рис. 1.7)

Рис. 1.7. Окно графика

М-файл функции. Работа из командной строки MatLab вызывает затруднения, если требуется вводить много команд и часто их изменять. Пусть, например, необходимо так задать в MatLab функцию , чтобы в дальнейшем её значение для, например, х = 7, можно было бы получить простым вызовомf(7) в командной строке − также как и для элементарных функций. Для этого в MatLab имеется простой механизм, называемый М-файл функция. Это, в сущности, аналог функций языков программирования. Сначала М-файл функцию надо создать. Для этого необходимо выполним щелчёк ЛКМ по иконке (New M-File − новый М-файл), находящейся в панели ярлыков (то же самое можно сделать выбрав меню File New M-File). Откроется окно редактора М-файлов и в нём, как показано на рис. 1.8, набираем текст функции (операции используем поэлементные!). Здесь function − обязательное служебное слово, с − имя переменной выходного параметра (если их более одного, то они через запятую записываются в квадратных скобках), f − имя функции, х − имя входной переменной (если их более одной, то они записываются через запятую). Комментарии в MatLab начинаются со знака процента и автоматически выделяются зелёным цветом. В этом же окне файл надо сохранить (щелчком ЛКМ по иконке, изображающей дискетку). Файл должен иметь то же имя, что и функция, а также тип m. В редакторе М-файлов может быть одновременно открыто несколько файлов. Переход между файлами осуществляется при помощи закладок с именами файлов, находящихся внизу окна редактора.

Рис. 1.8. Окно редактора М-файлов с функцией

Теперь имеется возможность вызывать функцию f, указывая конкретное значение её параметра, например

>> f(7)

ans =

243

Если имеется необходимость повторно вызвать функцию f, то это целесообразно сделать, используя клавиши <<>> и <<>>. Для получения справки по любой встроенной функции MatLab достаточно установить курсор на имя функции и нажать на клавишу <<F1>>.

Построим график приведенной выше функции f(x) в декартовых координатах для промежутка изменения аргумента [-0.2, 2] с шагом 0.2. Будем исходить из того, что М-файл для f(x) уже сохранён на диске. Подадим в командной строке две простые команды

>> x=[-0.2:0.2:2];

>> plot(x,f(x))

Результатом этих действий будет график, представленный на рис. 1.9,а. Если же подать следующие две команды

>> x=[-0.2:0.02:2];

>> plot(x,f(x))

то результат окажется несколько иным (см. рис. 1.9,б).

а) б)

Рис. 1.9. Окна графика функции f(x)

Решение системы линейных алгебраических уравнений (СЛАУ). Постановка задачи. Общий вид у СЛАУ следующий:

.

В матричном виде эта СЛАУ может быть записана в виде: , где

называется матрицей системы, − вектор-столбцом свободных членов или правых частей системы, а− искомым вектор-столбцом неизвестных системы. Решением СЛАУ является всякий вектор-столбецx, обращающий все уравнения системы в тождества.

Справедливо следующее утверждение. Если определитель основной матрицы СЛАУотличен от нуля, то система имеет единственное решение.

Рассмотрим порядок решения СЛАУ в MatLab на конкретном примере. Найти решение СЛАУ вида

Процесс решения будет выглядеть следующим образом

>> A=[7.9 5.6 5.7 -7.2;8.5 -4.8 0.8 3.5;4.3 4.2 -3.2 9.3;3.2 -1.4 -8.9 3.3]

A =

7.9000 5.6000 5.7000 -7.2000

8.5000 -4.8000 0.8000 3.5000

4.3000 4.2000 -3.2000 9.3000

3.2000 -1.4000 -8.9000 3.3000

>> det(A)

ans =

-1.0178e+004 % det А не равен нулю − решение единственное

>> b=[6.68;9.95;8.6;1]

b =

6.6800

9.9500

8.6000

1.0000

>> x=A\b

x =

0.9671

0.1248

0.4263

0.5679

>> A*x-b % вычисление невязки

ans =

1.0e-014 *

-0.0888

0.1776

0.1776

0.0444

Символ ‘\’ является оператором решения систем линейных уравнений.

Решение нелинейного уравнения. Нелинейным уравнением называется выражение вида , где - некоторая нелинейная функция. Корнем или решением уравнения называется всякое значение , обращающее уравнение в тождество, т. е. . В дальнейшем ограничимся рассмотрением лишь нелинейных уравнений с изолированными корнями, т. е. случая, когда для каждого корня уравнения существует окрестность, не содержащая других корней этого уравнения.

Функция , определённая и непрерывная на некотором конечном или бесконечном интервале , называется алгебраической, если она имеет вид , где - некоторые действительные или комплексные числа. К трансцендентным уравнениям относятся неалгебраические нелинейные уравнения.

К численным методам решения нелинейных уравнений приходиться обращаться в случае отсутствия у них аналитических выражений для решений или же если выполнение вычислений по ним является крайне трудоёмким делом.

Приближенное нахождение изолированных действительных корней обычно складывается из двух этапов:

1. отделение корней, т. е. нахождение возможно узких промежутков 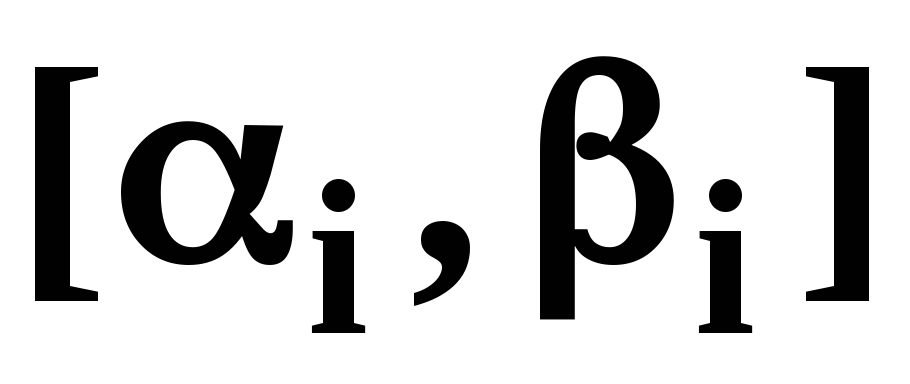, в которых содержится один и только один корень уравнения,i=1, 2, …;

2. уточнение приближенных корней, т. е. нахождение их положения с заданной степени абсолютной точности 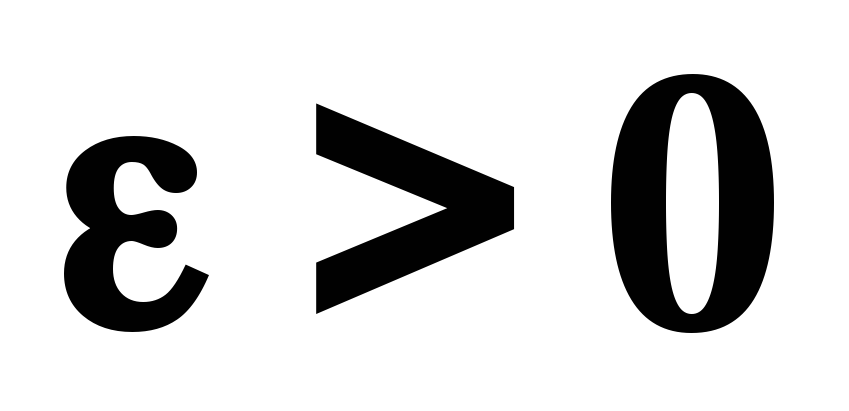. Под этим может пониматься выполнение одного из двух условий:или .

Для отделения корней полезна известная теорема существования корней нелинейного уравнения из математического анализа.

Теорема. Если непрерывная функция принимает значения разных знаков на концах отрезка , т. е. , то найдётся хотя бы одно число такое, что .

Корень заведомо будет единственным, если производная существует и сохраняет постоянный знак внутри интервала , т. е. если (или ) при .

Пример 1. Отделить корни уравнения на отрезке [-10, +10].

Решение.

>> x=[-10:0.01:10];

>> f=x.^3-6*x+2;

>> plot(x,f)

>> grid on % вызов функции grid с аргументом on приводит

% к появлению сетки на графике

Результат представлен на рис. 1.10,а. На нём видно, что у уравнения действительно имеется хотя бы один корень, но для более чёткого отделения корней желательно увеличить ту часть рисунка, что прилегает к оси абсцисс. Для этой цели следует использовать инструменты (Zoom In) и (Zoom Out), расположенные в графическом окне. В итоге получаем более удобное графическое представление (см. рис. 1.10,б), из которого следует, что корни уравнения находятся внутри отрезков [-3, -2], [0, 1] и [2, 3].

а) б)

Рис. 1.10. Отделение корней нелинейного уравнения

Для реализации второго этапа решения нелинейного уравнения вида в пакете MatLab имеется функция fzero, записываемая в различных видах:

− fzero(‘fun’,x) − возвращает уточнённое значение для х, при котором достигается нуль функции fun − имя М-файла, представленной строкой. х, стоящее вторым аргументом при вызове fzero, является начальным приближением к искомому корню. Примеры

>> fzero('cos',1)

ans =

1.5708

>> fzero('ff',-3)

ans =

-2.6017

В втором примере ff − это имя функции пользователя, которая должна быть оформлена в виде М-файла (см. рис. 1.11).

Рис. 1.11. Окно редактора М-файлов с функцией ff

− fzero(‘fun’,[x1 x2]) − возвращает уточнённое значение для х, находящееся внутри интервала (х1, х2). Должно выполняться условие fun(x1)fun(x2) < 0. Примеры

>> fzero('ff',[-3 -2])

ans =

-2.6017

>> fzero('ff',[0,1])

ans =

0.3399

− fzero(‘fun’,x,tol), fzero(‘fun’,[x1 x2], tol) − выполняют те же действия, что и ранее, но с заданной относительной точностью tol. Примеры

>> format long

>> fzero('ff',-3,1e-15)

ans =

-2.601679131883155

>> fzero('ff',[0,1],1e-10)

ans =

0.339876886623182

В зависимости от используемой формы функции fzero, MatLab реализует следующие методы поиска корня уравнения: метод дихотомии, метод секущих или метод обратной квадратичной интерполяции.