§ 1.6. Современная стоимость потока платежей с учетом риска

Количественный анализ потока платежей, в том числе расчет современной стоимости, обычно предполагает фиксированность размеров всех его членов и безусловность их выплат (см. расчетные формулы в § 1.2 и 1.3). В инвестиционных проектах, однако, часто сталкиваются со случаями, когда размер члена потока платежей является случайной переменной (размер заранее точно неизвестен) и задается в виде некоторого диапазона значений или среднего значения, например предполагаемый или ожидаемый уровень добычи минерального сырья, выпуск продукции при условии, что ее производство зависит от погодных условий или возможностей снабжения сырьем и т. д. Иногда проект предусматривает условия, согласно которым члены потока платежей (затраты и поступления) не являются безусловными, а лишь возможны (ожидаемы) с той или иной вероятностью. В частном случае такой поток представляет собой вероятностную или условную ренту. С подобного рода рентами встречаются и в страховании. В упомянутых случаях методики расчета современной стоимости и наращенной суммы по-

тока платежей нуждаются в существенных дополнениях. Эти методики выходят за рамки "классической" финансовой математики. Кратко рассмотрим две из возможных постановок задачи, зависящих от вида имеющейся информации о потоках платежей.

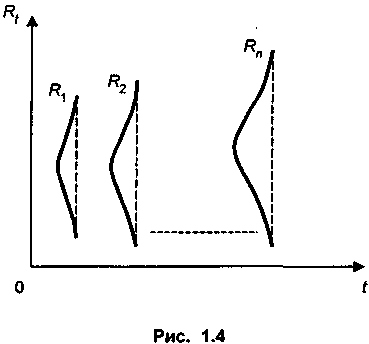
Члены потока платежей задаются статистическими распределениями. Пусть имеется поток платежей, выплачиваемых в моменты t = 1, ..., п. Каждый член потока является случайной величиной с заданным распределением. Вид и параметры распределения устанавливаются на основе имеющейся статистики или, что ближе к действительности, задаются экспертным путем. Таким образом, в целом поток платежей описывается последовательными распределениями случайных величин R_t.

Причем, чем больше срок платежа, тем, очевидно, больше амплитуда колебаний в размерах платежей (рис. 1.4). Обобщающее распределение показателя современной стоимости можно получить, суммируя частные распределения с соответствующим их дисконтированием. Распределения членов потока могут быть одинаковыми, что, разумеется, удобнее для расчетов, хотя и менее правдоподобно.

Для каждого из частных распределений нетрудно найти соответствующие средние . Величина современной стоимости потока, состоящего из средних, по определению, равна

(1.35)

где п_t — интервал от начала потока платежей до момента выплаты t-го члена потока.

Найденная по формуле (1.35) величина представляет собой среднюю распределения современной стоимости потока платежей, каждый из которых представлен в виде распределения. В частном случае, когда суммируемые распределения одинаковы на протяжении всего срока (соответственно одинаковы и их средние) и, кроме того, временные интервалы между платежами одинаковы, получим:

Фактическое значение современной стоимости потока платежей будет отличаться от расчетной средней . Различие будет тем больше, чем выше дисперсия распределения величиныА. Задача определения такой дисперсии в общем случае достаточно сложна. В связи с этим найдем, используя некоторые положения математической статистики, дисперсию суммарного распределения, но только для одного частного случая, анализ которого делает наглядным существо проблемы.

Допустим, что поток платежей описывается последовательными одинаковыми нормальными распределениями. Соответственно их средние и дисперсии одинаковы. Поскольку А представляет собой сумму дисконтированных величин (в данном случае Rv^t), то дисперсия каждого слагаемого этой суммы составит в силу известного свойства дисперсии величину D(Rv^t) = D(R)v^2t. Обозначим дисперсию частного распределения как D = D(R).

При условии независимости последовательных членов потока платежей (условие, следует заметить, сильно упрощающее действительное положение дел, однако позволяющее представить основные зависимости более наглядно) дисперсию суммы дисконтированных платежей (D₀) можно оценить как

(1.36)

Отсюда стандартное отклонение определяется как

(1.37) где и— стандартные отклонения распределенияА и R.

Сумма под корнем представляет собой своеобразный коэффициент приведения. Обозначим его d_n;i:

(1.38)

Полученная по формуле (1.36) дисперсия современной стоимости потока представляет собой нижнюю границу для величины дисперсии, так как здесь не учитывается возможная положительная корреляция между последовательными членами потока платежей. Как известно, такая корреляция слагаемых увеличивает дисперсию суммы.

Предположение о том, что частные распределения одинаковы, а еще лучше, являются нормальными, существенно упрощает анализ и позволяет решить одну важную задачу, а именно оценить с заданной вероятностью границы, в которых находится действительная величина современной стоимости потока платежей. Такие границы определяются как

где z — нормированное отклонение от средней (см. табл. 5 Приложения).

ПРИМЕР 17

Эксперты определили, что члены потока поступлений (рента постнумерандо) можно описать нормальными распределениями с параметрами 10 (средняя величина) и 3 (стандартное отклонение). Иными словами, полный диапазон значений каждого члена потока платежей укладывается в интервал, примерно равный 10 ± 3 х 3 . Срок поступлений — 5 лет. Дисконтирование производится по годовой ставке 15%. Допустим, что указанные распределения независимые, тогда

Границы диапазона современной стоимости такого потока платежей определяются выражением 32,52 ± z x 2,334.

Если вероятность, с которой желательно установить границы интервала, принята на уровне 90%, то z = 1,65 и искомые границы составят 28,72; 36,37. Уменьшение надежности вывода, естественно, сокращает этот интервал. Так, для вероятности 75% (z = 1,15) получим соответственно 29,84; 35,20.

Современная стоимость с учетом вероятностей выплат членов потока. В общей постановке задача выглядит следующим образом. Пусть выплата каждого члена потока платежей R_t не безусловна, а имеет некоторую вероятность р_t. Современная стоимость такого потока составит

(1.39)

Для практических целей данное выражение, очевидно, следует конкретизировать с учетом особенностей потока платежей в инвестиционном процессе или страховании. Например, пусть объектом является поток, состоящий из выплат премий (взносов страхователя) при долгосрочном страховании имущества. Обобщенную сумму премий в виде современной ее стоимости найдем, рассуждая следующим образом. Если страховое событие (например, гибель имущества) произойдет на первом году страхования, то страховщик получит премию только один раз; если это событие случится на втором году страхования, то премия будет выплачена два раза, и т. д. Допустим, что вероятности наступления страховых событий в течение года одинаковы и равны q. Если годовая премия пренумерандо равна Р, то математическое ожидание премии при дисконтировании ежегодных выплат за весь срок страхования составит:

где v — дисконтный множитель.

Полученный показатель Е(А) представляет собой современную стоимость страховых премий с учетом вероятности их выплат. Аналогичным путем можно разрабатывать формулы для оценки величины современной стоимости потоков платежей и для инвестиционных процессов, если учет вероятностей является необходимым.