§ 8.2. Методы определения интервальных прогнозов

После установления РВД и выбора вида распределения и уровня ДВ расчет границ интервального прогноза становится чисто технической задачей. Ее решение заключается в отсечении "лишних" концов РВД соответственно принятой доверительной вероятности. Иначе говоря, находят величины

А = а + х; B =b - x ,

где x — величина, зависящая от вида распределения и вероятности неудачи (неосуществления прогноза); очевидно, что упомянутая вероятность равна 1 - ДВ. Площади под кривой распределения, отсекаемые от "хвостов", равны половине этой вероятности (см. рис. 8.2) для треугольного распределения:

. (8.1)

Значения этой вероятности для некоторых уровней ДВ приведены в табл. 8.1.

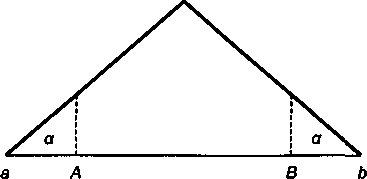
Рис. 8.2

Таблица 8.1

ДВ, %	60	70	75	80	90
a	0,2	0,15	0,125	0,1	0,05

Из сказанного следует, что задача определения интервального прогноза сводится к расчету размера x. Методики разработаны для следующих ситуаций:

А. Объект прогнозирования — отдельная количественная характеристика. Эксперт указывает РВД, вид распределения, а для распределения Тр и интервал наиболее вероятных значений прогнозируемого показателя.

Б. Прогноз суммы показателей, . Например, сумма объемов выпуска нескольких видов продукции. Для каждого слагаемого указывается РВД и вид распределения. ДВ назначается только для итоговой суммы.

В. Прогноз произведения двух показателей, Y = vw. Например, произведение "нормативного" и объемного показателей. Эксперт указывает РВД, вид распределения и ДВ для каждого сомножителя.

На первый взгляд представляется, что обсуждаемую методику легко распространить на прогноз суммы произведений. Формально это несложно выполнить. Однако, как показали расчеты, степень "сжатия" прогнозного интервала в этих условиях весьма мала, так что применение данной методики не имеет смысла.

Покажем технику применения перечисленных методик для каждого из указанных распределений вероятностей.

Методика а. Расчет интервального прогноза отдельной характеристики

Распределение N.

Известно, что площадь под кривой нормального распределения в пределах примерно равна 99%. Отсюда

,

где М — средняя,

—стандартное (среднее квадратическое) отклонение.

Пусть z — нормированное отклонение от средней⁴³, зависящее от выбранной доверительной вероятности. Тогда нормированное значение искомой величины x составит:

, (8.2)

где

u = 3 - z. (8.3)

Вероятности невыполнения прогноза в каждом "хвосте" нормального распределения составят:

. (8.4)

Заметим, что для нормального распределения ДВ = F(z).

В табл. 8.2 ⁴⁴ приводятся значения z, и, в зависимости от уровня ДВ.

Таблица 8.2

ДВ(%)	68	75	80	85	90	95
Z	1	1,15	1,28	1,44	1,65	1,96
U	2	1,85	1,72	1,54	1,35	1,04
	0,16	0,125	0,1	0,075	0,05	0,025

Необходимое для расчета по формуле (8.2) значение находим следующим образом:

. (8.5)

Распределение Т.

Искомая величина находится как функция от L и :

. (8.6)

Распределение Тр.

Здесь возможны два варианта. Если , то

, (8.7)

где l = М₂ - М₁ .

Если же , то

, (8.8)

Распределение Р.

. (8.9)

ПРИМЕР 1

Ожидается, что РВД (допустим, речь идет о годовом размере добычи минерального сырья) оценивается экспертом в объеме 1,2 — 1,8 млн. т. Определим интервальный прогноз для всех перечисленных выше видов распределений при условии, что ДВ = 80%. Для принятого уровня доверительной вероятности = 0,1.

Распределение N. L = 1,8 - 1,2 = 0,6; = 0,6/6 = 0,1; u = 1,72 (см. табл. 8.2). По формуле (8.2) получим

x = 1,72 x 0,1 = 0,172.

Таким образом, прогнозный интервал имеет пределы:

А = 1,2 + 0,172 = 1,37; B = 1,8 - 0,172 = 1,63.

Распределение Т. По формуле (8.6) находим

x = 0,6 х =0,134 ,

откуда

A = 1,2 + 0,134 1,33; B = 1,8 - 0,134 1,67.

Распределение Тр. Пусть интервал наиболее вероятных значений находится в пределах 1,35-1,65, l = 0,3. Поскольку

,

применяется формула (8.7):

;

А = 1,2 + 0,12 = 1,32; В = 1,8 - 0,12 = 1,68.

Распределение Р.

x = 0,1 х 0,6 = 0,06;

А = 1,2 + 0,06 = 1,26; В = 1,8 - 0,06 = 1,74 .

Как видим, распределения N, Т и Тр дали примерно одинаковые интервалы для прогноза, а распределение Р — более "размытый" вариант.