§ 2.5. Налог на имущество и выбор модели износа

Налог на имущество зависит от двух параметров — остаточной стоимости имущества и установленной налоговой ставки. В свою очередь, его остаточная стоимость определяется сроком амортизации и принятым методом (моделью) начисления износа.

Для начала определим общую сумму налогов за весь срок их выплат (срок амортизации) без приведения к начальному моменту времени (обозначим эту сумму N). Для этого обратимся к линейной модели, в которой L = 0. Общность вывода от этого не пострадает. Для сроков амортизации, равных двум и трем годам, имеем:

где Т — налоговая ставка.

Из приведенных формул следует вывод: увеличение срока амортизации неизбежно приводит к росту суммы налога на имущество.

Зависимость суммы налогов от срока можно представить и аналитически. Проще всего это сделать для линейной модели. Суммарная величина налога на имущество в общем виде определяется как

где N_t — налог в конце года t;

B_t — остаточная стоимость на конец года до очередного списания износа.

Определим остаточную балансовую стоимость для линейной модели и выполним ряд преобразований. В результате для случая, когда L = 0, находим простую зависимость:

(2.23)

Влияние срока здесь представлено в явном виде — каждый год прироста срока увеличивает общую сумму налога на величину, равную РТ/2. Для общего случая, когда L > 0, зависимость суммы налогов от срока получим (см. § 2.6) в виде

(2.24)

Зависимость общей суммы налогов от срока амортизации и здесь остается линейной. Заметим, что ликвидационная стоимость увеличивает эту сумму.

Обсуждение данной проблемы будет неполным, если не учесть моменты времени, когда выплачивались налоги. Для этого дисконтируем налоговые платежи по некоторой процентной ставке i. Для линейной модели при сроке два и три года получим

где V — приведенная сумма налога;

v — дисконтный множитель по ставке i.

Как видим, и в этом случае вариант с меньшим сроком оказывается предпочтительным для налогоплательщика.

Очевидно, что выбор модели износа также влияет на общую сумму налоговых платежей. Аналитическое сравнение приведенных сумм налогов для разных применяемых моделей износа и сроков амортизации не столь элементарно, как это было сделано выше для линейной модели. Проще на основе конкретных данных подсчитать и сравнить соответствующие величины, тем более что результат сравнения зависит и от уровня применяемой для дисконтирования процентной ставки.

§ 2.6. Математическое приложение

а. Доказательство формулы (2.16) Исходное равенство

Находим долю остаточной стоимости в амортизируемой сумме:

Поскольку и , то

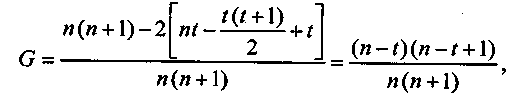
откуда

б. Доказательство соотношения

в. Доказательство формулы (2.24)

Остаточная стоимость в конце года t до очередного списания износа определяется как

B_t = P - D(t - 1).

Соответственно

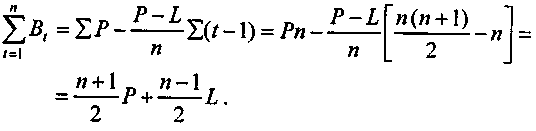
И, наконец,

Глава 3 определение барьерных значений экономических показателей

Вы, профессор, воля ваша, что-то нескладное придумали! Оно, может, и умно, но больно непонятно. Над вами потешаться будут.

М. Булгаков § 3.1. Общая постановка задачи. Линейная модель

В практике финансово-экономического анализа довольно часто возникает необходимость определить барьерное (критическое, предельно допустимое) значение некоторого параметра. Под барьерным значением параметра понимается такая его величина, превышение которой приводит к положительному или отрицательному конечному экономическому результату в рамках некой производственной или финансовой системы. Например, если речь идет об определении объема производства какого-то продукта, то критическим его значением является такой объем выпуска, при котором полученная прибыль равна нулю. Превышение этого объема дает прибыль, производство в меньшем объеме оказывается убыточным. Подобная и многие другие, сходные по общей постановке задачи решаются с помощью метода барьерной (критической) точки (break-even analysis). Этот метод широко используется в финансовом проектировании, при разработке бизнес-планов и при решении ряда финансовых проблем.

Наиболее простая постановка задачи осуществляется с помощью линейной модели. Разумеется, такая постановка не является единственно возможной. Некоторые пути для дальнейшего развития метода предлагаются в следующих параграфах главы. Причем часть из рассмотренных здесь проблем, например, барьерные точки для налоговых ставок и барьерные точки в условиях неопределенности, до сих пор не обсуждалась в финансовой литературе.

Заметим, что до недавнего времени метод барьерной точки применялся в статическом варианте. Экономические показатели рассматривались в рамках одного, сравнительно короткого периода. В последнее время делаются попытки применить метод к потокам платежей, охватывающим ряд последовательных временных интервалов. В этих случаях с помощью дисконтирования стал учитываться важнейший фактор — время (а именно сроки инвестирования и сроки отдачи от инвестиций).

Для начала рассмотрим наиболее простой и весьма условный вариант статической постановки задачи, к которому обычно прибегают при объяснении сути метода. Пусть необходимо найти критический объем производства одного вида продукта при условии, что все необходимые для анализа количественные зависимости описываются линейными выражениями, иначе говоря, применяется линейная модель.

Для записи такой модели примем обозначения:

Q — объем производства в натуральном или условно-натуральном измерении;

F — постоянные производственные затраты, затраты, не зависящие от объема выпуска;

с — пропорциональные затраты (в расчете на единицу продукции);

p — цена единицы продукции;

S — общая сумма затрат;

V — стоимость выпущенной продукции;

P — размер прибыли до уплаты налогов.

Переменные Q, F, S, V, Р определяются в расчете на одинаковый интервал времени, обычно на один год.

Для начала найдем стоимость выпущенной продукции и соответствующую сумму затрат:

V = pQ; (3.1)

S = F + cQ. (3.2)

Искомый критический объем производства или барьерную точку (break-even point) получим на основе равенства стоимости выпущенной продукции и суммы затрат: V = S . Именно равенство двух разнородных экономических показателей, каждый из которых является функцией управляющего параметра (в рассматриваемом случае — объема производства), лежит в основе метода барьерной точки.

Обозначим барьерный объем производства Q_k. Тогда, используя (3.1) и (3.2), получим

pQ_k = cQ_k + F.

Таким образом,

(3.3)

Как видим, значение барьерной ставки пропорционально постоянным затратам и обратно пропорционально разности цены и величины переменных затрат. При уменьшении этой разности величина барьерной точки ускоренно возрастает.

Прибыль (до выплаты налогов) по определению составит:

P = V - S = (p - c)Q - F. (3.4)

Графическая иллюстрация постановки задачи и ее решения приведена на рис. 3.1. Решение находится в точке пересечения двух линий, одна из которых характеризует динамику затрат S, другая — изменение дохода V по мере увеличения выпуска. Объемы производства, которые меньше критического Q_k , приведут к убыткам. Превышение этого объема дает прибыль (линия P). Чем выше размер постоянных и переменных затрат, тем больше критический объем производства. Прибыль после уплаты налогов (пропорциональных прибыли) характеризуется на рис. 3.1 пунктирной линией M.

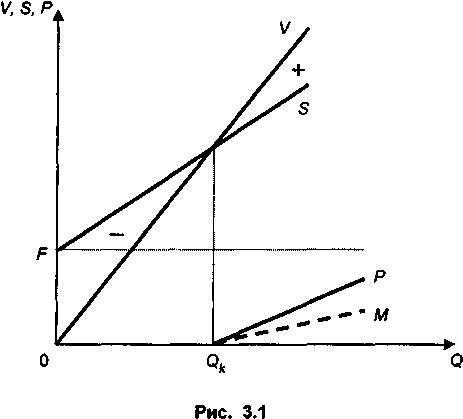
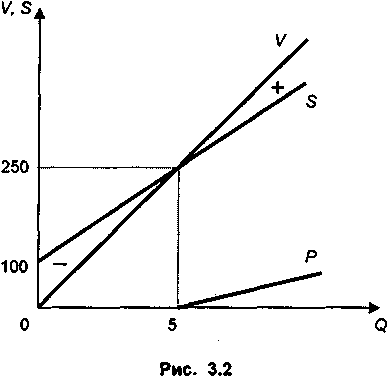
ПРИМЕР 1

Ожидается, что р = 50, с = 30, F = 100. Находим

, Р = (50 - 30)Q - 100.

Графическое изображение условий задачи и ее решение представлены на рис. 3.2.

Рассмотренный метод базируется на реальных данных бухгалтерского учета или ожидаемых их величинах. Капиталовложения учитываются посредством включения в затраты амортизационных отчислений. Заметим, что все участвующие в расчете параметры рассматриваются как константы. Между тем с течением времени они, безусловно, изменяются, и найденная для одного момента времени критическая точка не окажется таковой для другого момента. Важно также подчеркнуть, что время как важнейший финансовый фактор не принимается здесь во внимание. Такой подход вполне оправдан, если капиталовложения уже осуществлены и встает вопрос только о выборе видов производимой продукции и их объемов.

Сказанное выше позволяет сформулировать общее определение для обсуждаемого метода как способа расчета барьерного значения управляющего параметра исходя из равенства двух "конкурирующих" функций этого параметра. Содержание управляющего параметра и функций, как видим, определяется конкретными условиями решаемой задачи. В рассмотренном примере управляющим параметром является объем производства, "конкурирующими" функциями — доход (выручка) и затраты.

Вариантом рассмотрения задачи является определение минимально допустимого срока выпуска продукции при заданных годовых объемах производства, т. е. срока окупаемости. Объем производства выступает здесь как параметр, а срок выпуска — как управляющая переменная. Вместо годовых постоянных затрат учитывается общий размер инвестиций и сопряженных затрат (параметр F). Тогда "конкурирующие" функции имеют вид

V = nQp; S = F + nQc,

где n — срок выпуска.

Барьерный срок окупаемости n_k (методы расчета срока окупаемости для разных ситуаций рассматриваются в гл. 6) определяется как

(3.5)