ФНПВар6

Вариант № 6

1. Найти область определения функции и изобразить её на плоскости: .

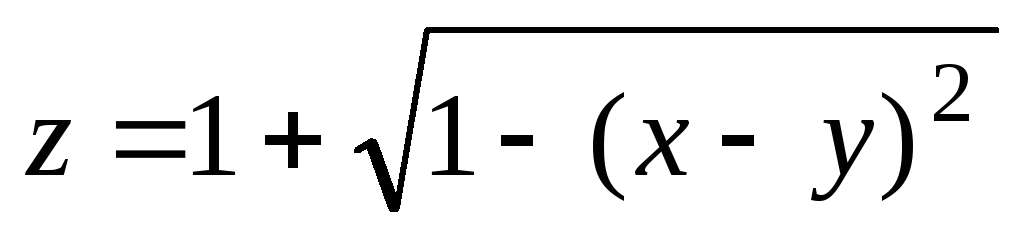Для заданной функции область определяется следующим неравенством: . Преобразуем неравенство: или . Эти неравенства определяют область, заключённую между прямой и прямой , т.е. между прямыми и . Границы области входят в область определения функции (см. рисунок). Ответ: .

2. Вычислить частные производные и сложной функции в данной точке: при .

Частные производные сложной функции двух переменных находятся по формулам и . В данном случае . Следовательно, ,

. Заметим, что в точке промежуточные переменные равны: . Подставляя в частные производные , получим: , . Ответ: , .

3. Найти уравнение касательной плоскости и нормали к указанной поверхности в данной на ней точке: .

Касательная плоскость и нормаль к поверхности в точке имеют следующие уравнения: а) (касательная плоскость): (нормаль). В данном случае . Найдём частные производные от в точке : . Подставим найденные частные производные в уравнения касательной плоскости и нормали: , . Или , . Ответ: а) Уравнение касательной плоскости: ; б) Уравнение нормали: .

4. Найти наибольшее и наименьшее значения функции в области D: .

Н айдём стационарные точки в области D: . Решая систему , получим стационарную точку . В этой точке . На границе области D , , функция имеет вид . Тогда . Точка экстремума . В этой точке . На границе области D , функция имеет вид . Тогда . Точка экстремума . На границе функция имеет вид . Или Тогда . Точка экстремума . В этой точке . Находим значение функции в угловых точках области D: . Сравнивая все значения , видим, что наибольшее значение функция принимает в точке , а наименьшее значение - в точке . Ответ: наибольшее значение функции в точке , наименьшее значение - в точке .

5. Изменить порядок интегрирования: .

В осстановим область интегрирования (D) по пределам повторных интегралов: , . Изобразим область интегрирования на чертеже (см. рисунок). Найдём точки пересечения линий и : . Порядок интегрирования в данном интеграле показан штриховкой на первом графике. На втором графике штриховка изменена на вертикальную. Из рисунка видим, что данная область является y – трапецией. На нижней границе , на верхней границе . Поэтому и в результате подстановки пределов получим следующий повторный интеграл: . Ответ: .

6. Найти объём тела, ограниченного указанными поверхностями: .

Основанием тела в плоскости ХОУ является область D, ограниченная параболой и прямой . Снизу тело ограничено плоскостью , сверху – поверхностью (см. рисунок). Таким образом,

. Ответ: .

7. Найти объём тела, ограниченного указанными поверхностями: .

Преобразуем уравнения цилиндрической поверхности: . Сверху тело ограничено поверхностью параболоида вращения , а снизу – координатной плоскостью (см. рисунок). Удобно перейти к цилиндрическим координатам: . Уравнением окружности будет , уравнением параболоида будет . При найдём точки пересечения окружностей и , получаем: . Область интегрирования будет область . Следовательно, . Ответ: .

8. Найти объём тела, ограниченного указанными поверхностями: .

Воронка разрезана, заключённая между двумя сферическими поверхностями, плоскостями и . Тело представляет часть воронки, заключённой между этими плоскостями. Снизу воронка ограничена конической поверхностью , сверху – конической поверхностью . Перейдём к сферической системе координат: . Якобиан преобразования равен . Уравнение малой сферы будет , большой сферы - , На плоскости будет , а на плоскости будет или . Уравнение малого конуса переходит в уравнение , а большого конуса – в уравнение . Таким образом, тело занимает следующую область: . Объём тела равен: . Или . . Ответ: .

9. Н айти массу пластинки:

Пластинка занимает область D, изображённую на рисунке. Область неудобна для интегрирования в декартовой системе координат. Поэтому перейдём к эллиптической системе координат: . Уравнением меньшего эллипса будет: . Аналогично, для большего эллипса получим: . Якобиан преобразования равен . На прямой линии имеем . Область, занимаемая пластинкой, есть . Тогда . Ответ: .

10. Найти массу тела: .

Тело представляет часть цилиндра, «вырезанную» изнутри конической поверхностью, и ограниченную плоскостями и . Цилиндрическая поверхность пересекается с поверхностью конуса на высоте (см. рисунок). Область интегрирования: . Интегрирование в декартовой системе координат неудобно. Перейдём к цилиндрической системе координат: . Таким образом, тело занимает следующую область: . При этом плотность тела равна . Масса тела равна: . Или . Ответ: .

11. Вычислить криволинейный интеграл по формуле Грина: .

Преобразуем криволинейный интеграл по замкнутому контуру в двойной по формуле Грина: . Область интегрирования изображена на рисунке. Для заданного интеграла получаем: . Действительно, в эллиптических координатах якобиан преобразования равен . Следовательно, . Ответ: .

12. Вычислить массу дуги кривой (L) при заданной плотности :

.

М ассу дуги вычисляем с помощью криволинейного интеграла первого рода: . В данном примере линия и плотность заданы в полярных координатах, где . Следовательно, . Ответ: .

13. Вычислить работу силы при перемещении вдоль линии от точки M к точке N: .

Работу вычисляем по формуле: . Линия представляет собой окружность, являющуюся пересечением цилиндрической поверхности и поверхности параболоида вращения . Линия расположена в плоскости (см. рисунок). Перейдём к параметрическому заданию линии: . Найдём значение параметра t, при котором достигаются точки M и N; ; . Тогда

. Ответ: Работа равна .

14. Найти производную функции в точке по направлению внешней нормали к поверхности , заданной уравнением , или по направлению вектора : .

Производная по направлению находится по формуле: , где - координаты единичного вектора данного направления. Найдём частные производные функции в заданной точке: . Следовательно, . Найдём координаты вектора ,

где :

. Таким образом, . Найдём единичный вектор нормали : . Так как координата z вектора положительна, то нормаль является внешней (см. рисунок). Тогда производная по заданному направлению равна: . Ответ: .

15. Найти наибольшую скорость изменения скалярного поля в заданной точке М: .

Наибольшую скорость характеризует градиент поля: .

Вычислим координаты градиента: , , . Таким образом, .

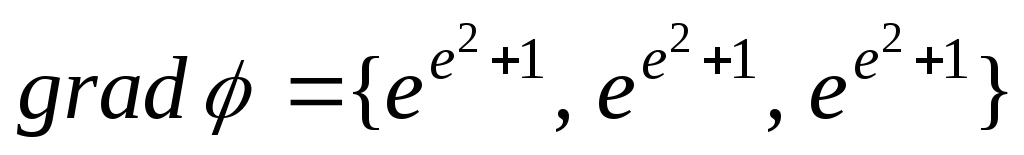Величина скорости есть модуль градиегнта: .

Ответ: Наибольшая скорость изменения поля в заданной точке равна .

16. Вычислить расходимость и вихрь в произвольной точке М, а также найти уравнения векторных линий поля градиента скалярного поля : .

По заданному скалярному полю построим поле его градиентов: . Дивергенция (расходимость) вектора определяется формулой: . Для градиента получаем: . Ротор вектора вычисляется как символический определитель третьего порядка:

. Для поля градиентов :

.

Уравнение векторных линий поля определяется системой дифференциальных уравнений: . Для заданного поля :

. Из равенства следует или .

Рассмотрим равенство . Исключая отсюда , получим . Или . Таким образом, уравнения векторных линийполя градиентов задаётся как семейство кривых от пересечения следующих поверхностей:. Ответ: , , урвнения векторных линий поля градиентов: .

17. Найти поток векторного поля через часть плоскости Р, расположенную в 1-ом октанте (нормаль образует острый угол с осью OZ): .

З апишем уравнение плоскости в отрезках: или и изобразим её на чертеже (см. рис.). Найдём нормальный вектор: . Нормируем нормальный вектор: . Поток векторного поля находится по формуле , где - проекция вектора поля на нормаль к поверхности: . Поверхностный интеграл сведём к двойному интегралу по области D, являющейся проекцией Р на координатную плоскость ХОУ: . При этом . Из уравнения поверхности . Тогда .

Ответ: .

18…19. Тело Т лежит в 1-ом октанте и ограничено плоскостями координат и поверхностью Q, заданной уравнением . Вычислить:

а) поток поля вектора через поверхность, ограничивающую тело Т (воспользоваться формулой Остроградского);

в) циркуляцию поля вектора вдоль линии пересечения поверхности Q с плоскостями координат в направлении от точки пересечения Q с осью ОХ к точке пересечения Q с осью OY ( воспользоваться формулой Стокса): .

Решение.

а ) Линии пересечения поверхности с координатными плоскостями.