Выбор u и dV.

1. ∫x^ksinaxdx итд. За U(х) берём x^k, а за dV sinax, e^ax итд

2. ∫x^klnxdx, ∫x^karcsinxdx. За U(x) берём трансцендентную функцию, а за dV x^k

3. ∫e^axsinbxdx. За U(x) берём e^ax, а за dV sinx/cosx ДВАЖДЫ!

∫e^2xsinxdx = (e^2x(2sinx-cosx)/5)+C

Билет 32. Рациональные дроби. Разложение рациональной дроби на простейшие дроби. Интегрирование простейших дробей. Интегрирование рациональных дробей.

Многочлен – алгебраическое выражение вида a₀+a₁x+a₂x²…a_nxⁿ

Рациональная дробь. Обозначим P_m(x) и Q_n(x) многочленами степени m и n. Рациональная дробь R(x) – отношение двух этих многочленов: R(x) = P_m(x)/Q_n(x). Если дробь правильная, то m<n, если неправильная, то m>=n. Если дробь неправильная, то можно выделить целую часть делением числителя на знаменатель уголком.

Разложение рациональной дроби на простейшие. Qn(x) = an*(x1-c1)^ν1*(x2-c2)^ν2*(xl-cl)^νl*(x2+px+q_n) ^νn (1)

Правильную рациональную дробь можно разложить на сумму простейших дробей 4 типов:

A/(x-a), A/(x-a)^k, (Mx+N)/(x²+px+q), (Mx+N)/(x²+px+q)^k

В разложении P_m(x)/Q_n(x) на элементарные дроби сомножителю (x-a)^k будет соответствовать сумма k дробей вида A1/(x-a) + A2/(x-a)² + … + Ak/(x-a)^k (метод неопределённых коэффициентов)

Интегрирование простейших дробей.

Интегрирование рациональных дробей. Неопределённый интеграл от нерациональной дроби существует на любом промежутке, где её знаменатель не обращается в 0 и представляется в виде суммы рациональных функций, log, arctg итд.

Схема интегрирования рациональных дробей.

1. Если дробь неправильная – выделить целую часть

2. Найти все корни знаменателя и его разложение на множители по формуле (1)

3. Разложить рациональную дробь на сумму простейших

4. Проинтегрировать каждую из простейших дробей согласно её типу, результаты просуммировать

Билет 33. Интегрирование тригонометрических выражений.

1) ∫R(sinx, cosx)dx

Подстановка tg(x/2)=t, sinx = 2t/(1+t²), cosx = (1-t²)/(1+t²), dx = 2dt/(1+t²)

2) ∫R(sinx, cosx)dx

Подстановка tgx=t, sinx = t/(корень из 1+t²), cosx = 1/(корень из 1+t²), dx = dt/(1+t²)

3)∫R(sinx)cosxdx

Подстановка sinx=t, cosxdx = dt

4)∫sin^2mxcos²ⁿxdx

Подстановка cos²x = (1+cos2x)/2, sin²x = (1-cos2x)/2, sinxcosx = 1/2sin2x

5)∫sin^mxcosⁿxdx

n=2k+1, (cos2x)^k , затем подстановка sinx = t

6)∫sinαx sinβx = ½(cos(α-β)x – cos(α+β)x;

∫cosαx cosβx = ½(cos(α-β)x + cos(α+β)x;

∫ sinαx cosβx = ½(sin (α-β)x + cos(α+β)x

Билет 34. Интегрирование иррациональых функций.

1. ∫R(x, (ax+b/cx+d)^r1/s1)dx

Интеграл берётся с помощью замены ax+b/cx+d = t^N, где N – наименьший общий знаменатель дробей

2. ∫R(x, (корень из a²-x²)dx, a = sint

3. ∫R(x, (корень из a²+x²)dx, a = tgt

4. ∫R(x, (корень из x²-a²)dx, a = a/cost

5. Дифференциальный бином: x^m(axⁿ+b)^pdx

1) p – целое

2) m+1 – целое, подстановка axⁿ+b=t^s, где p=r/s

3) m+1/n+p – целое, подстановка axⁿ+b=t^sxⁿ,

6) Подстановки Эйлера R(x, (корень из ax²+bx+c)

1) Если а>0, то корень из ax²+bx+c = t+-кор. из ах

2) Если а<0, то корень из ax²+bx+c = xt+-кор. из c

3) Если ax²+bx+c имеет различные действительные корни х1 и х2, то корень из ax²+bx+c = t(x-x1)

Билет 35. Нахождение пути по скорости. Интеграл Римана. Алгебраические свойства интеграла. Свойства, связанные с отрезками интегрирования. Интегральные неравенства и оценки, 1-я теорема о среднем.

О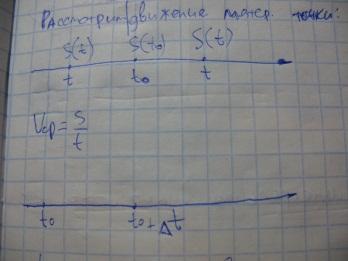пределение пути по заданной скорости. S=Vt (равномерное прямолинейное движение). Рассмотрим движение материальной точки. ∆t – малый промежуток времени. V(t) ≈ V(t0).

∆S=S(t0+ ∆t)-S(t0). Разобьём промежуток [t0; t] на n частей: [t0; t1] итд. и обозначим

∆k = t_k-t_k-1. Тогда приближённый путь равен: S(t)-S(t0) = ∆S ≈ V(T1)(t1-t0) + V(T2)(t2-t1)

и т.д., если max ∆k0, D и E∆S

О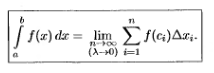пределение. Пусть f(x) задана на [a; b] и пусть существует конечное I такое, что для для любого ε>0 найдётся δ>0 такая, что |I- δ |< ε при условии, что параметр разбиения с отмеченными точками λ (P; ξ)< δ . Тогда функция называется интегрированной по Римену на [a;b], число I называют пределом инт.

Пределы интегрирования.