6.6. Использование моделей

В качестве примера использования модели с координатными осями dиqрассмотрим синхронную явнополюсную машину с двумя полюсами на роторе и обмоткой якоря на статоре. Осьdнаправлена по оси полюсов ротора и содержит обмоткуd₂(обмотку возбуждения), осьdне содержит обмоток на роторе. Пусть машина работает в генераторном режиме, когда напряжения на обмотках якоря не прикладываются извне, а определяются суммой ЭДС за вычетом падений напряжения на сопротивленииRв каждой обмотке, т.е.

.

Допустим далее, что режим стационарный, т.е. р=0, и с учетом сделанных замечаний перепишем уравнения в виде

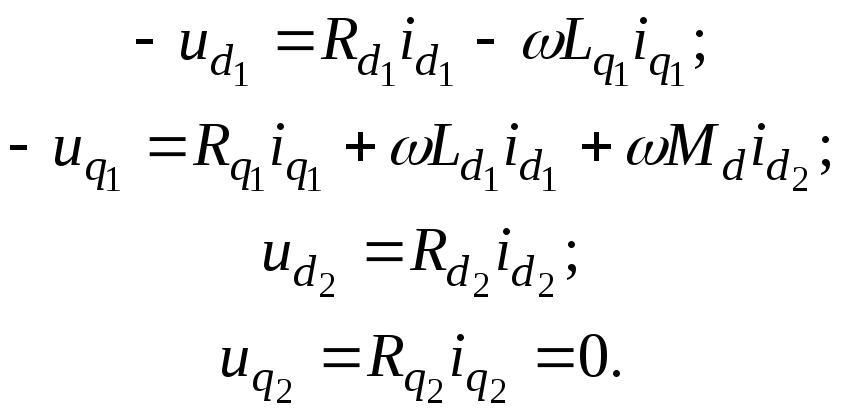
Введем обозначения:

.

Параметры X_dиX_q– индуктивные сопротивления якоря по продольной и поперечной осям соответственно. Величина_0т – амплитудное значение ЭДС вращенияпри холостом ходе, когда. Первые два уравнения запишутся в виде

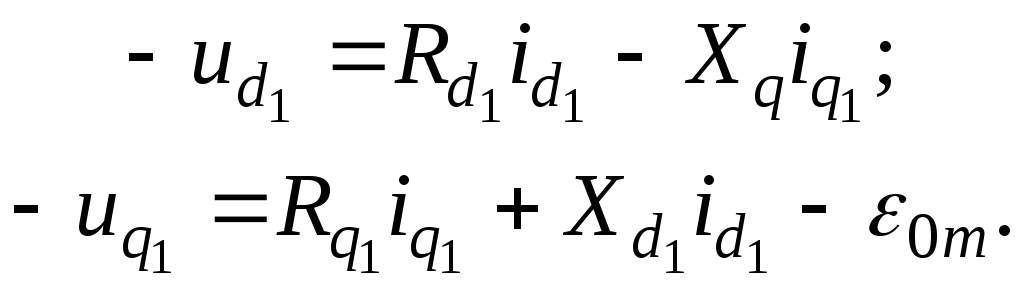
Напряжения и токи реальных неподвижных статорных обмоток могут рассматриваться как проекции на оси обмоток изображающих векторов и, вращающихся относительно статора с угловой частотой.

Так как оси dиqв данном случае вращаются в ту же сторону с той же частотой, векторыинеподвижны относительно осейdиq, а их проекции на эти оси связаны уравнениями.

Если принять, что на оси dоткладываются действительные, а на осиq– мнимые числа, тоиможно представить так:

.

Умножая первое уравнение на (-1), второе - на (-j) и суммируя их, при, опуская для упрощения индекс «1» у напряжений и токов.

В результате получится

.

Этому уравнению соответствует пространственная векторная диаграмма в комплексной плоскости, приведенная на рисунке. Хотя эта диаграмма построена на основе пространственных изображающих векторов, она идентична обычной векторной диаграмме синхронного генератора, поскольку в обоих случаях мгновенные значения параметров определяются как проекции вращающихся векторов на некоторые неподвижные оси.

Угол нагрузки на диаграмме характеризует сдвиг по фазе междуи, а также пространственный сдвиг между осями потока возбужденияФ₀и полного потока якоряФ(при пренебреженииR).

Момент М_эмдля рассматриваемой машины, пренебрегая влиянием активных сопротивлений обмоток (), определяется с учетом проекций векторов

;

.

Подставляя и переходя к действующим значениям ₀,U, получится:

.

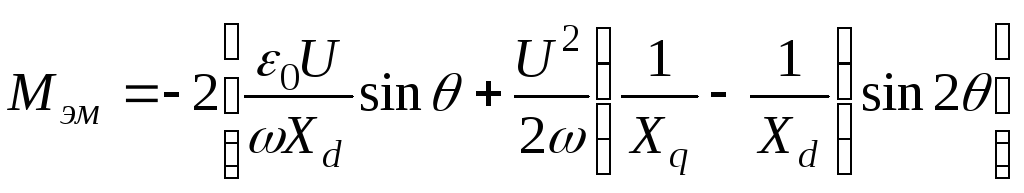Знак минус перед правой частью показывает, что в генераторном режиме электромагнитный момент является тормозным.

В теории синхронных машин часто выбирают положительное направление М_эмпротивоположным по отношению кМ_мех, т.е. считаютМ_эм>0,>0 в генераторном режиме иМ_эм<0,<0 в двигательном режиме.

Если синхронная машина имеет тфаз (а не две фазы, как в рассмотренном случае), то перед квадратной скобкой вместо 2 стоит множительт. Таким образом, с помощью модели с (d,q)-координатами получают более полную формулу для электромагнитного момента, чем формула для неявнополюсной модели в (,)-координатах, в которой учет магнитной несимметрии затруднителен.

Таким образом, модель машины с осями dиqописывается системой дифференциальных уравнений с постоянными коэффициентами, что существенно упрощает ее анализ по сравнению с предыдущей моделью. Кроме того, модель с осямиdиqпозволяет легко учесть явнополюсную конструкцию электрической машины.

Модель ЭМП с (d,q)-координатами позволяет эффективно исследовать переходные процессы в динамических режимах синхронной машины. В таких режимах помимо якорной обмотки и обмотки возбуждения важную роль играют демпферные обмотки.

Модель с полюсами на роторе, дополненная короткозамкнутыми демпферными обмотками на осях dиq.

Полная система уравнений Парка-Горева для статорных обмоток якоря на осях dиq,обмотки возбуждения ротора на осиdи роторных демпферных обмоток на осяхdиqзапишется в виде

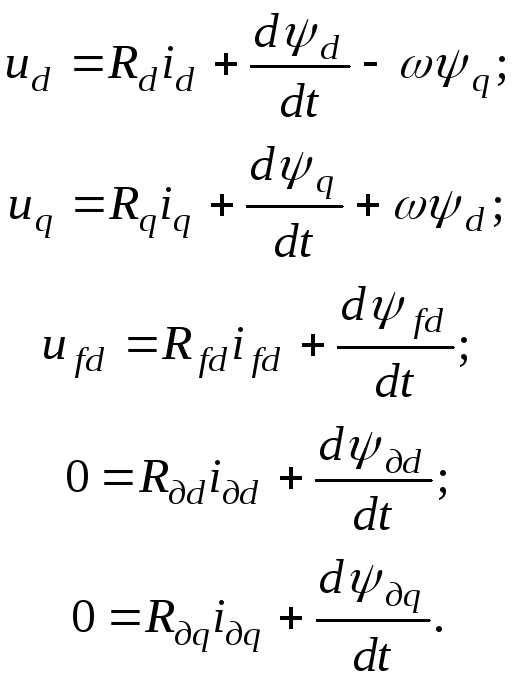
Считая, что обмотки ротора приведены к обмоткам статора, можно выразить потокосцепления обмоток статора и ротора в виде

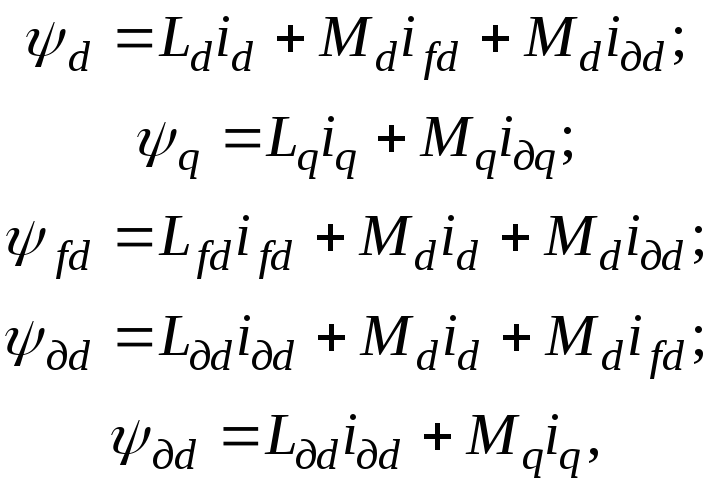
где LиМ– полная индуктивность обмотки и взаимная индуктивность между обмотками на соответствующих осях.

Ясно, что Lопределяется полным потоком, сцепленным с обмоткой,М– потоком взаимной индукции. Поэтому разностиL – M=L_соответствуют потокам рассеяния обмоток, т.е.

Т.к. все обмотки неподвижны, то LиМ–const, т.к. это первые пространственные гармоники поля. Поэтому система уравнений Парка-Горева приводится к системе с постоянными коэффициентами и может решаться операторным методом относительно неизвестных токовi_dиi_q.