
- •В. А. Тюков
- •Утверждено редакционно-издательским советом
- •Введение в теорию систем
- •1. Общие сведения об электромеханических системах
- •1.2. Процесс преобразования энергии
- •1.3. Электромеханические преобразователи энергии
- •1.4. Составы автоматических систем
- •1.5. Обобщенная структура электропривода
- •1.6. Электродвигатели для эмс
- •1.7. Преобразовательные устройства
- •1.8. Управляющие устройства. Способы управления эмс
- •1.10. Подбор типа редуктора
- •2.2. Общая характеристика устройства эмп
- •2.5. Принцип работы мпт
- •2.6. Принцип действия см
- •3. Электромагнитный момент эмп
- •3.1. Общие сведения.
- •3.2. Взаимодействие двух обмоток
- •3.3. Взаимодействие магнитных полей
- •3.4. Определение электромагнитного момента по изменению энергии.
- •3.5. О динамике электромагнитного момента.
- •3.6. Факторы нестабильности момента в системах с индукционными двигателями
- •3.7. Новые методы определения электромагнитного момента трехфазных асинхронных двигателей
- •3.8. Пульсационность электромагнитного момента
- •3.9. Динамический электромагнитный момент
- •4.2.Связь магнитного поля в воздушном зазоре с током обмотки
- •4.3. Обмоточная функция
- •4.4. Потокосцепление и индуктивность обмотки
- •4.5. Анализ обмоток.
- •4.6. Пространственные вектора
- •4.8. Многофазные обмотки
- •Используя равенство
- •Направление вращения полей гармонических в воздушном зазоре
- •5. Элементы общей теории эмп
- •5.1. Независимые величины и их производные
- •5.2. Превращение энергии в элементе проводника
- •5.3. Движение элемента под действием электромагнитной силы
- •5.4. Процессы в неподвижном элементе
- •6.1. Общий подход к математическому описанию эмс
- •6.2. Изображающие пространственные вектора
- •6.3. Обобщенные модели эмп
- •6.4. Обобщенная модель с взаимно вращающимися осями координат
- •6.5. Обобщенная модель с взаимно неподвижными осями координат
- •6.6. Использование моделей
- •6.7. К определению параметров обобщенного эмп
- •6.8. Использование уравнений Лагранжа для описания электромеханических преобразователей
- •7. Управление потоком энергии в эмс
- •7.2. Моменты и силы сопротивления в эмс
- •7.3. Способы, законы и системы управления в эмс
- •7.4. Рациональное распределение передаточных чисел
- •7.5. Оценка передаточного числа редуктора по быстродействию
- •7.6. Оценка передаточного числа редуктора по минимуму массы и стоимости модуля
- •7.7. Оценка передаточного числа по нагреву и целесообразности применения редуктора
- •7.10. Особенности работы дпт при питании выпрямителя
- •7.11. Энергодинамические характеристики силовой части приводов постоянного тока
- •7.12. Распределение потока энергии в индукционных двигателях
- •7.13. Законы регулирования частоты вращения
- •7.14. Машина двойного питания
- •7.16. Совместимость преобразователя и двигателя в эмс
- •7.22. Законы регулирования электропривода с частотным управлением
- •7.23. Расчет механических характеристик частотно-регулируемого
- •7.26. Математическая модель дпт при вариации способа возбуждения
- •О выборе типа эмс
- •2. Электромеханические преобразователи
- •3. Электромагнитный момент эмп
6.2. Изображающие пространственные вектора
и преобразование координат
Как
следует из предыдущего, для математического
описания ЭМС необходимо знать о
пространственных (изображающих) векторах
![]() и
и![]() .
Выбором угловой скоростиk(частота вращения системы координат)
привязывает всю систему к тому или
иному обобщенному вектору.
.
Выбором угловой скоростиk(частота вращения системы координат)
привязывает всю систему к тому или
иному обобщенному вектору.
Как известно, для гармонически изменяющихся величин (в том числе U,Iи т.д.) применяется символический (комплексный) метод. Суть его всем хорошо известна. Представление исследуемых величин на комплексной плоскости системой вращающихся, но взаимно неподвижных векторов. Например, мгновенные значенияUпредставляются в виде:
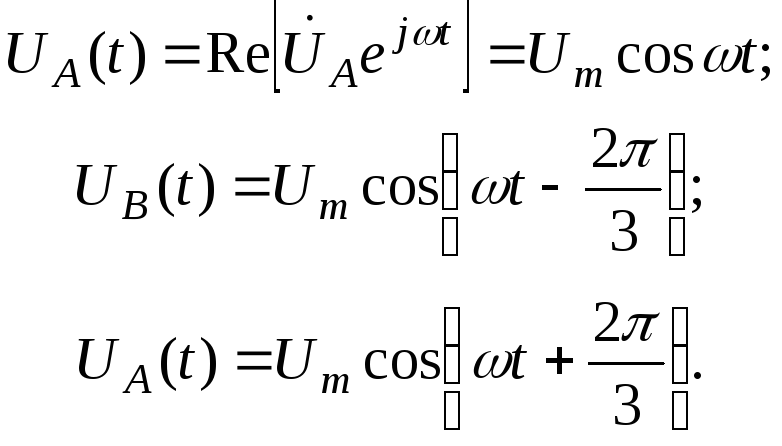

графическом аналитическом
и их проекции на действительную ось представляют мгновенные значения напряжений фаз часто необходимо описать гармонически с помощью пространственных вращающихся векторов в физической плоскости, связанной с вращающейся частью.
Представим систему: неподвижная трехфазная обмотка и вращающийся со скоростью двухполюсный индуктор сФт–constи системой координатd-q.d– ось полюсов, продольная ось,q– геометрическая нейтраль, поперечная ось. Осьdсдвинута относительно фазы А на угол=t.
П ри
вращенииФтсоздает в
фазах обмотки потоки (потокосцепления)
ри
вращенииФтсоздает в
фазах обмотки потоки (потокосцепления)
![]() ;
;
![]()
![]() ,
,
а так как
![]() ,
то отстает от потока на
,
то отстает от потока на![]() и
и
![]() ;
;
![]() ;
;
![]()
и будет направлена по оси q.
ЭДС
![]() создает
создает![]() ,
который в данном случае отстает от ЭДС
на пространственный угол.
Получится цепочка
,
который в данном случае отстает от ЭДС
на пространственный угол.
Получится цепочка
![]()
Напряжение опережает Iна угол, зависящий отrихобмотки.
Вектора
![]() и т.д., проекции которых на оси якорных
обмоток определяют мгновенные
гармонические значения, называют
изображающими векторами.
и т.д., проекции которых на оси якорных
обмоток определяют мгновенные
гармонические значения, называют
изображающими векторами.
Очевидно, что их
расположение на физической плоскости
повторяет расположение соответствующих
комплексов на обычной векторной
диаграмме в комплексной плоскости и в
то же время каждый изображающий вектор
имеет проекции на оси d-qи может представляться с их помощью,
т.е.![]() .
.
При совмещении
физической плоскости с комплексной
обычно ось d принимают
действительной, аq– мнимой и тогда![]() и т.д. Это позволяет переходить от одной
системы координат к другой.
и т.д. Это позволяет переходить от одной
системы координат к другой.
П редставим
две системы координатА-В-Сиd-q.- угол сдвига
системыd-qот системыА-В-С. Для вектора токаIm,
сдвинутого от оси фазыАна угол,
можно записать
редставим
две системы координатА-В-Сиd-q.- угол сдвига
системыd-qот системыА-В-С. Для вектора токаIm,
сдвинутого от оси фазыАна угол,
можно записать
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Поскольку cos() можно представить выражением
![]() аsin()
аsin()
![]() ,
,
то, если =t, получим переводные соотношения для токовidиiqчерез токиiA,iB,iC:
![]() ;
;
![]()
или
![]()
и, соответственно, обратный переход сопровождается необходимостью проекций iA,iB,iCна осиА,В,С. В результате получим
![]() ;
;
![]() ;
;
![]() .
.
Естественно, аналогичные формулы верны при преобразовании МДС, ЭДС, напряжений, потоков и т.д.
Подобные преобразования часто позволяют существенно упростить математические модели за счет замены систем дифференциальных уравнений с переменными коэффициентами на системы с постоянными коэффициентами.
В общем случае можно предположить, что есть две ортогональные системы d-qи-, вращающиеся относительно друг друга. Еслиd-qповернута относительно-на уголпротив часовой стрелки, то зависимости между проекциями, например, тока, выглядят:
![]()
Так же связаны проекции
других величин. Ясно, что преобразование
на основе изображающих векторов
справедливо при симметричных системах,
т.е. если сумма мгновенных значений
iA+iB+iCвсегда равна нулю, что верно для обмоток,
соединенных в звезду. В общем случае
при значении iA+iB+iC0
анализ усложняется применением метода
симметричных составляющих, где появляется
нулевая составляющая![]() .
.
