
MMATAN02
.pdf
Из неравенства | sin(x − x0)| < |x − x0| следует, что функция sin(x −x0) есть бесконечно малая функция при x → x0. А так как | cos(x + x0 −3)| ≤ 1, то α(x) также бесконечно малая при x → x0, как произведение ограниченной функции на бесконечно малую
функцию. Откуда следует, что lim sin(2x − 3) = sin(2x0 − 3).
x→x0
3. В точке x = 5 функция f (x) = √ |
|
определена: f (5) = 3. |
|
x + 4 |
|||
Зададим ε > 0. Составим разность f (x) − f (5) = |
√ |
||
x + 4 − 3 и |
|||
оценим ее по модулю. При малых δ > 0 для значений x, таких, что |x − 5| < δ, будет выполняться неравенство
|
√ |
|
|
|
|
|
|
|
|
x |
|
5 |
|
|
x |
5 |
|
|
|
δ |
|
|
|
|
x + 4 |
|
3 |
|
= |
|
| − |
|
|
| |
< |
| − |
|
| |
< |
|
|
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
| |
|
|
|
|
− |
|
| |
|
√x + 4 + 3 |
3 |
|
|
|
3 |
|
|
|||||||
Если положить |
δ |
= ε, т.е. δ = 3ε, то при значениях x, для ко- |
|||||||||||||||||||||
|
|||||||||||||||||||||||
3 |
|||||||||||||||||||||||
торых |x − 5| < 3ε, выполняется неравенство |
|
√ |
|
|
|
− 3| < ε. |
|||||||||||||||||
| |
x + 4 |
||||||||||||||||||||||
Непрерывность функции f (x) = |
√ |
|
|
|
|
|
|
= 5 доказана. |
|||||||||||||||
|
|
x + 4 в точке x |
|||||||||||||||||||||
4.а) Нет, так формулировать нельзя. Если взять ε отрицательным,
то |f (x) − f (x0)| не может быть меньше ε < 0, каким бы ни выбрали δ > 0 и какую бы функцию f (x) ни рассматривали.
б) Нет. В этой формулировке не сказано, что δ > 0. Если мы
положим δ < 0, то множество x, для которых |x − x0| < δ, пусто, а поэтому для всех таких x выполняется любое свойство, в том
числе и |f (x) − f (x0)| < ε. Значит, при таком определении все функции окажутся непрерывными.
5. Возьмем любое значение x R и дадим ему приращение x.
Получим новое значение аргумента x + x. При этом функция x
y = 1 + x2 получит следующее приращение y:
y = f (x + x) |
− f (x) = |
x + x |
|
− |
x |
||||
|
|
|
|||||||
1 + (x + x)2 |
1 + x2 |
||||||||
= x + x3 + x + x2 x − x − x3 − 2x2 |
x − x(Δx)2 |
||||||||
|
|
[1 + (x + x)2](1 + x2) |
|
|
|
|
|||
= |
|
|
x − x2 x − x(Δx)2 |
. |
|
|
|
||
|
[1 + (x + x)2](1 + x2) |
|
|
|
|||||
|
|
|
|
|
|
|
|||
=
=
101

При любом фиксированном x |
R |
мы имеем |
lim |
y = 0 |
. Значит, |
||
|
x 0 |
|
|||||
функция f (x) = |
x |
|
|
|
→ |
|
|
|
непрерывна на всей числовой оси. |
||||||
1 + x2 |
|||||||
6.Прежде всего заметим, что элементарные функции, изучаемые в школе, непрерывны всюду в своей области определения. Поэтому каждое слагаемое в числителе функции
f (x) = (x2 − 3) · 2x + arctg x · cos x , (x3 + 1) sin3 x
есть непрерывная функция при всех значениях x R как произведение непрерывных функций. Сумма двух непрерывных функций непрерывная функция. Знаменатель тоже непрерывная функция при всех действительных значениях x как произведение непрерывных функций. Знаменатель обращается в нуль x = −1 и x = kπ, k Z. Значит, рассматриваемая функция f (x) будет непрерывной при всех значениях x R, кроме x = −1 и x = kπ, k Z, где она не определена.
7. а) Область определения функции
|
|
1 |
(2x2 + 3) |
при − ∞ < x ≤ 1, |
||
|
|
|||||
f (x) = |
5 |
|||||
|
|
|
6 |
− |
5x |
при 1 < x < 3, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 3 при 3 ≤ x < +∞,
—вся числовая ось (−∞, +∞). На интервалах (−∞, 1), (1, 3), (3, +∞) функция непрерывна. Поэтому разрывы возможны лишь в точках x = 1 и x = 3, в которых изменяется аналитическое задание функции. Найдем односторонние пределы функции в точке x = 1:
f (1 |
− |
0) |
= |
lim |
|
1 |
|
(2x2 |
+ 3) = 1, |
|
0 |
5 |
|
||||||||
|
|
x |
1 |
|
|
|
||||
|
|
|
|
→ − |
(6 |
|
5x) = 1. |
|||
f (1 + |
0) |
= x |
lim |
− |
||||||
1+0 |
|
|
|
|
||||||
|
|
|
|
→ |
|
|
|
|
|
|
Значение функции f (x) в точке x = 1 определяется первым ана-
литическим выражением, f (1) = 2 + 3 = 1. Так как f (1 − 0) = 5
f (1 + 0) = f (1), то в точке x = 1 функция f (x) непрерывна.
102

Рассмотрим точку x = 3. Имеем |
|
|
|
|
|
||
f (3 − 0) |
= x |
lim |
(6 |
− |
5x) = |
− |
9, |
3 0 |
|
|
|
||||
|
|
→ − |
|
|
|
|
|
f (3 + 0) |
= |
lim |
|
|
|
|
|
|
x |
3+0(x − 3) = 0. |
|
||||
|
|
→ |
|
|
|
|
|
Так как f (3 − 0) = f (3 + 0) и конечны, то функция f (x) в точке x = 3 имеет разрыв 1-го рода.
Колебание функции f (x) в точке x = 3 равно
|f (3 − 0) − f (3 + 0)| = 9.
б) Функция |
3x |
при x > 3 |
|
||
f (x) = −2x2 |
при x ≤ 3, |
|
определена и непрерывна в интервалах (−∞, 3) и (3 + ∞). В точке x = 3 имеем
f (3 |
− |
0) |
= |
lim |
2 |
) = −18, |
|
||||||
|
|
|
x 3 0(−2x |
|||
|
|
|
|
→ − |
|
|
f (3 + 0) |
= |
lim 3x = 9. |
||||
|
|
|
|
x→3+0 |
|
|
Так как f (3 − 0) = f (3 + 0) и конечны, то функция f (x) в точке x = 3 имеет разрыв 1-го рода.
Колебание функции в точке x = 3 равно
|f (3 + 0) − f (3 − 0)| = 27.
в) Функция |
|
|
|
|
f (x) = |
|2x − 3| |
|
|
|
2x − 3 |
3 |
|
||
|
|
|||
определена и непрерывна при x −∞, |
. Рассмотрим точку |
|||
|
||||
2 |
||||
|
|
|
103 |
|

3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
|
. Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
f |
3 |
|
− |
0 |
= |
lim |
|
|2x − 3| |
= |
lim |
|
−(2x − 3) |
= |
− |
1, |
||||||||||||
|
|
2 |
|
|
2x − 3 |
2x − 3 |
|||||||||||||||||||||||
|
|
|
|
x→2 −0 |
|
|
|
|
|
x→2 −0 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
2x − 3 |
|
|
|
3 |
|
2x − 3 |
|
|
|
||||||||
2 |
|
|
|
|
|
x→2 +0 |
|
|
|
|
|
x→2 +0 |
|
|
|
|
|||||||||||||
|
|
f |
3 |
+ 0 |
= |
lim |
|2x − 3| |
= |
lim |
|
2x − 3 |
= 1. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
Так как f |
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
− |
0 = f |
|
|
+ 0 и конечны, то функция f (x) в |
||||||||||||||||||||||||
2 |
2 |
||||||||||||||||||||||||||||
точке x = |
3 |
|
имеет разрыв 1-го рода. |
|
|
|
|
|
|
||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||
Колебание функции в точке x = |
3 |
|
равно |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
+ 0 |
= 2. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
f 2 − 0 − f |
2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. При x = 1 функцию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = |
|
|
− |
|
|
|
при x = 1, |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5− |
|
|
|
при x = 1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
можно переписать в виде: f (x) = x+1, и, следовательно, функция f (x) при любом значении x = 1 будет непрерывной. При x = 1
f (1 − 0) = f (1 + 0) = 2 = 5 = f (1).
Значит, в точке x = 1 функция f (x) имеет устранимый разрыв. Достаточно переопределить функцию, положив f (1) = 2, и функция станет непрерывной всюду на действительной оси.
9. Функция
|
1 |
при x = 0, |
f (x) = |
e x |
|
|
0 |
при x = 0 |
|
|
|
104

непрерывна при всех x = 0. При x = 0 имеем
|
|
1 |
|
1 |
|
|
f (−0) = xlim |
0 e |
x = 0, |
f (+0) = lim |
x = + |
∞ |
. |
|
x +0 e |
|
|
|||
→− |
|
|
→ |
|
|
|
В точке x = 0 функция имеет разрыв 2-го рода типа бесконечного скачка (бесконечный разрыв).
10. Функция |
|
|
|
|
|
|
|
|
|
|
|
f (x) = |
1 + 2x |
при x ≤ 0, |
|||||||||
|
|
|
sin 1 |
|
при x > 0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x = 0 |
|
|||
|
x = |
0 |
|
|
|
|
|
|
|||
непрерывна при всех |
|
|
|
|
|
|
|
имеем |
|||
|
|
|
. При |
|
|
||||||
f (−0) = xlim0(1 + 2x) = 2, |
|||||||||||
|
|
→− |
|
1 |
|
|
|
|
|||
f (+0) = |
lim |
|
sin |
|
|
— не существует. |
|||||
|
x |
|
|||||||||
|
|
x→+0 |
|
|
|
|
|||||
В точке x = 0 функция имеет разрыв 2-го рода.
Задачи для самостоятельной работы
1. Исходя из определения непрерывности ( lim f (x) = f (x0)), дока-
зать непрерывность функций
x→x0
a) f (x) = |
|
x3 + x − 1 |
||||
|
2x2 + 3x − 5 |
|||||
|
|
|||||
б) f (x) = |
|
x2 cos x |
|
|
||
|
1 + sin2 x |
|||||
|
|
sin x |
x = 0 |
|||
в) f (x) = |
|
|
||||
x |
||||||
|
|
1 |
|
x = 0 |
||
|
|
|
|
|
|
|
в интервале 2 < x < 3,
для всех x (−∞, +∞),
для всех x (−∞, +∞).
105

2.Исходя из определения непрерывности по Коши, доказать непрерывность функций
а) f (x) = |
|
x + 3 |
1 |
|
||||
|
|
|
|
|
в точке x = |
|
, |
|
|
2 − 3x |
2 |
||||||
б) f (x) = |
√ |
|
|
для всех x > 0, |
||||
|
|
x |
||||||
в) f (x) = sin x |
для всех x R. |
|||||||
3. Пользуясь определением непрерывности функции через приращение аргумента и функции ( lim y = 0), доказать непрерывность
x→0
функций
а) f (x) = |
√3 |
|
|
для |
x (−∞, +∞), |
|
|||||
x |
|||||
б) f (x) = arcsin x |
для всех x (−1, 1), |
||||
в) f (x) = 2x |
для |
x (−∞, +∞). |
|||
4.Исследовать на непрерывность, найти точки разрыва и установить их характер:
а) f (x) = cos |
π |
, |
||||
2 − x |
||||||
б) f (x) = |
|
|
1 |
, |
|
|
|
x2 − 9 |
0 < x ≤ 1, |
||||
в) f (x) = |
1 − x |
|||||
|
|
x |
x ≤ 0, |
|||
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − x |
x > 1. |
|||
|
|
|
|
|
|
|
Ответы
4. а) x = 2 — точка разрыва 2-го рода, б) x = ±3 — точки разрыва 2-го рода, в) x = 1 — точка разрыва 2-го рода, x = 0 — точка разрыва 1-го рода.
106
Занятие 8. Непрерывность функции. Односторонняя непрерывность. Разрывы на графике функции
Задание
1. Исследовать функцию
ln |x| при − ∞ < x < 0,
f (x) =
x при 0 ≤ x ≤ 1,
x2 + 1 при 1 < x ≤ 2,
5 при 2 < x < +∞
на непрерывность, найти точки разрыва и установить их характер. Построить график функции.
2. Найти точки разрыва функции
f (x) = |
|x|x−2 |
x |
при x = 0, |
|
|
|
|
|
|
|
|
0 |
|
при x = 0, |
установить их род, исследовать функцию на одностороннюю непрерывность, построить график функции.
3. Исследовать функцию |
|
|
|
|
f (x) = |
|
1 |
при x = 0, |
|
x arctg x |
||||
|
|
1 |
|
при x = 0, |
|
|
|
||
на непрерывность, найти точки разрыва и определить их характер. Построить график функции.
4.Функция f (x) не определена в точке x = 0. Определить значение f (0) так, чтобы f (x) стала непрерывной при x = 0, если
107

√
а) f (x) = √1 + x − 1 ,
3 1 + x − 1
в) f (x) = 23x − 1 , x
б) f (x) = ln(1 − 3x) , x
г) f (x) = arcsin x .
Решения
1. Функция
ln |x| при − ∞ < x < 0,
f (x) =
x при 0 ≤ x ≤ 1,
x2 + 1 при 1 < x ≤ 2,
5 при 2 < x < +∞
задана различными формулами на нескольких промежутках. В каждом из промежутков x < 0, 0 < x < 1, 1 < x < 2, x > 2 функция непрерывна. Следовательно, разрыв может быть только в точках x = 0, x = 1, x = 2. Рассмотрим каждую точку в отдельности:
1) x = 0
lim f (x) = lim ln |x| = −∞.
x→−0 x→−0
Значит, в точке x = 0 функция f (x) имеет разрыв 2-го рода. При этом
lim f (x) = lim x = 0 = f (0),
x→+0 x→+0
т.е. функция f (x) непрерывна справа в точке x = 0. 2) x = 1
f (1 |
lim f (x) = |
lim x = 1 = f (1), |
− 0) = x 1 0 |
x 1 0 |
|
|
→ − |
→ − |
f (1 + 0) = lim f (x) = |
lim (x2 + 1) = 2. |
|
|
x→1+0 |
x→1+0 |
Отсюда следует, что x = 1 есть точка разрыва 1-го рода. Так как предел слева в точке x = 1 равен значению функции в этой точке, то функция f (x) непрерывна слева в точке x = 1.
108
3) x = 2
f (2 |
lim f (x) = |
lim |
(x2 + 1) = 5, |
− 0) = x 2 0 |
x 2 0 |
|
|
|
→ − |
→ − |
|
f (2 + 0) = lim f (x) = |
lim |
5 = 5, |
|
|
x→2+0 |
x→2+0 |
|
f (2) = (x2 + 1) x=2= 5.
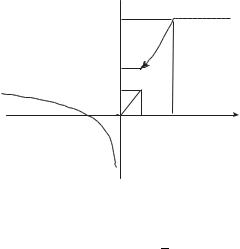
Значит, в точке x = 2 функция непрерывна. График функции изображен на рис. 3.1.
y 
5
2
1
-1 |
1 |
2 |
x |
Рис. 3.1
2.При x < 0 функция f (x) = −x2 . При x > 0 f (x) = 0. Отсюда следует, что функция f (x) непрерывна в интервалах (−∞, 0) и (0, +∞). Найдем односторонние пределы функции f (x) в точке x = 0.
− |
|
x→−0 f (x) = x→−0 |
−x |
= +∞, |
||
f ( 0) |
= |
lim |
lim |
2 |
|
|
|
|
|
||||
f (+0) |
= |
lim f (x) = lim |
0 = 0 = f (0). |
|||
|
|
x→+0 |
x→+0 |
|
|
|
Таким образом, функция f (x) имеет в точке x = 0 разрыв 2-го рода, при этом она является непрерывной справа в точке x = 0. График функции изображен на рис. 3.2.
109
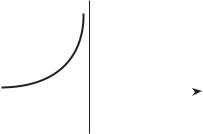
y
|
|
0 |
|
|
|
|
|
|
x |
|
|
|
Рис. 3.2 |
|
|
|
|
|
|||
3. В интервалах (−∞, 0) и (0, +∞) функция |
|
|
|
|
||||||
|
|
1 |
при x = 0, |
|
||||||
|
f (x) = x arctg x |
|
||||||||
|
|
1 |
|
при x = 0, |
|
|||||
|
|
|
|
|||||||
непрерывна. При x = 0 имеем |
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|||
f (−0) = xlim0 f (x) = xlim0 x arctg |
|
= 0, |
||||||||
x |
||||||||||
|
→− |
|
|
|
→− |
1 |
|
|||
f (+0) = lim |
f (x) = |
lim x arctg |
= 0. |
|||||||
x |
||||||||||
|
x→+0 |
|
|
x→+0 |
|
|||||
Значение функции f (x) в точке x = 0 равно f (0) = 1, а f (−0) = f (+0). Следовательно, функция имеет в точке x = 0 устранимый разрыв.
Отметим также, что график функции f (x) имеет горизонтальную асимптоту y = 1, так как
lim |
f (x) = |
lim x arctg |
1 |
= 1. |
||||
x |
||||||||
x→±∞ |
x→±∞ |
|
||||||
График функции изображен на рис. 3.3 |
|
|
||||||
4. а) Функция |
|
√ |
|
|
− 1 |
|
|
|
|
f (x) = |
1 + x |
|
|
|
|||
|
|
√3 1 + x − 1 |
|
|
||||
110 |
|
|
|
|
|
|
|
|
