
матан 2 семестр
.docx
Практические задания
Задание №1
Вычислить определитель матрицы
|
|
Матрица |
|
1 |
|
|
2 |
|
Задание №2
|
|
Решить матричное уравнение |
|
1 |
|
|
2 |
|
Задание №3
Установить, является данная система линейных уравнений совместной или несовместной:
|
|
Система |
|
1 |
|
|
2 |
|
Задание №4
|
|
Решить систему уравнений: а) по правилу Крамера; б) методом обратной матрицы; в) методом Гаусса. |
|
1 |
|
|
2 |
|
Задание №5
|
|
Найти общее решение системы уравнений. Привести одно частное решение. |
|
1 |
|
|
2 |
|
Задание №6
Обувная фабрика
специализируется по выпуску изделий
трех видов: сапог, кроссовок и ботинок.
В производстве обуви используется сырье
трех типов:
 .
Нормы расхода каждого из типов сырья
на одну пару обуви заданы матрицей
.
Нормы расхода каждого из типов сырья
на одну пару обуви заданы матрицей
 ,
i,j=1,2,3,
а объем
расхода сырья на 1 день задан вектором
,
i,j=1,2,3,
а объем
расхода сырья на 1 день задан вектором
 :
:
|
Вид сырья |
Нормы расхода сырья на одну пару (усл.ед.) |
Расход сырья на 1 день (усл.ед.) |
|||
|
Сапоги |
Кроссовки |
Ботинки |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти ежедневный объем выпуска каждого вида обуви.
|
|
Данные задачи. |
|
1 |
|
|
2 |
|
Задание №7
С двух заводов
поставляются автомобили для двух
автохозяйств. Заводы выпустили
 и
и
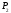 автомобилей соответственно, автохозяйствам
требуется
автомобилей соответственно, автохозяйствам
требуется

 и
и
 автомобилей
соответственно, причем
автомобилей
соответственно, причем
 .
Затраты на перевозку машин с заводов в
каждое автохозяйство задаются матрицей
.
Затраты на перевозку машин с заводов в
каждое автохозяйство задаются матрицей
 (см. таблицу).
(см. таблицу).
|
Автохозяйство Завод |
Затраты на перевозку в автохозяйство (ден. ед.) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти план перевозок машин, если затраты на перевозку составили F ден. ед.
|
|
Данные задачи |
|
1 |
|
|
2 |
|
Задание №8
|
|
При
каком значении
|
|
1 |
|
|
2 |
|
Задание №9
|
Номер варианта |
Решить задачу |
|
1 |
В треугольнике
|
|
2 |
В треугольнике
|
Задание №10
|
|
Вычислить
площадь параллелограмма, построенного
на векторах
|
|
1 |
|
|
2 |
|
Задание №11
|
|
Определить,
при каких значениях
|
|
1 |
|
|
2 |
|
Задание №12
|
|
Доказать,
что точки
|
|
1 |
. |
|
2 |
|
Задание №13
|
|
Для
треугольника
|
|
1 |
|
|
2 |
|
Задание №14
|
|
Даны две вершины треугольника М1 и М2, а его высоты пересекаются в точке N. Найти координаты вершины М3 треугольника. |
|
1 |
М1(-1,0), М2(2,1), N(0,2) |
|
2 |
М1(3,1), М2(-1,1), N(-1,2) |
Задание №15
|
|
Составить уравнение плоскости, проходящей через т. А, В и С, найти расстояние от точки М до этой плоскости и координаты точки N, симметричной точке М относительно этой плоскости. |
|
1 |
А(3,1,0), В(-1,3,5), С(2,0,2), М(1,3,2) |
|
2 |
А(-5,1,2), В(0,1,5), С(1,0,2), М(1,-1,2) |
Задание №16
|
|
Определить,
при каком
|
|
1 |
П:
|
|
2 |
П:
|
Задание №17
|
|
Написать каноническое уравнение прямой, полученной при пересечении двух заданных плоскостей: |
|
1 |
2x + y + z - 2 = 0 2x – y - 3z + 6 = 0 |
|
2 |
x - 3y - 2z + 3 = 0 3x - y + 2z = 0 |







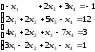

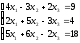






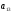







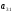






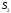






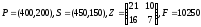

 векторы
векторы
 и
и
 ортогональны.
ортогональны. {1,3,2},
{1,3,2},
 {3,0,–1},
{3,0,–1},
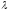
 +2
+2 ,
,
 3
3 –
– .
. {4,3,1},
{4,3,1},
 {3,–2,1},
{3,–2,1}, 2
2 +7
+7 ,
,
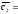

 –
– .
. известны координаты точек
известны координаты точек
 ,
,
 ,
и
,
и
 ,
где
,
где
 –
середина стороны
–
середина стороны
 .
Найти расстояние от начала координат
до точки
.
Найти расстояние от начала координат
до точки ,
угол между векторами
,
угол между векторами
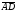 и
и
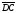 и
и
 .
. известны координаты вершин
известны координаты вершин
 и
и
 и координаты точки пересечения медиан
и координаты точки пересечения медиан
 .
Найти расстояние от начала координат
до вершины
.
Найти расстояние от начала координат
до вершины
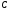 ,
угол
,
угол
 и
и
 .
. и
и
 .
. 4
4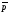 +2
+2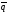 ,
,
 =6
=6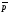 –
–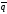 ,
,
 3
,
3
,
 1,
1,
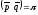 /6
/6 2
2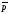 +
+ ,
,
 =
= –5
–5 ,
,
 5,
5,
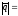 1,
1,

 и
и
 вектора
вектора
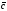 и
и
 коллинеарны.
коллинеарны. =32
=32 +
+
 +
+
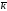 ,
,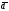 =
=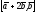 ,
где
,
где
 ={–4,6,1},
={–4,6,1}, ={5,2,3}
={5,2,3} =
=
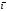 –
–
 +46
+46 ,
,
 =
=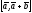 ,
где
,
где
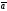 ={2,5,–1},
={2,5,–1}, ={–3,4,1}
={–3,4,1} ,
,
 ,
,
 ,
,
 не лежат в одной плоскости, вычислить
объем тетраэдра
не лежат в одной плоскости, вычислить
объем тетраэдра
 и длину высоты, опущенной на грань
и длину высоты, опущенной на грань
 .
. (–2,7,4),
(–2,7,4),
 (5,1,8),
(5,1,8),
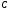 (2,1,–1,),
(2,1,–1,), (–1,2,1).
(–1,2,1).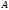 (5,2,1),
(5,2,1),
 (3,2,0),
(3,2,0),
 (5,3,9),
(5,3,9), (2,7,1).
(2,7,1). ,
заданного координатами его вершин,
найти общее уравнение его высоты,
опущенной из вершины
,
заданного координатами его вершин,
найти общее уравнение его высоты,
опущенной из вершины
 .
. ,
,
 ,
,
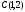 .
. ,
,
 ,
,
 .
. плоскость
П: параллельна прямой L:
.
плоскость
П: параллельна прямой L:
. ,
L:
,
L:

 ,
L:
,
L:
