1.5.2. Метод характеров неприводимых представлений.

Для применения теории групп необходимо знать неприводимые представления, для которых волновые функции молекулы являются базисными функциями. Их можно определить из таблиц характеров неприводимых представлений, известных из теории групп.

Можно доказать, что для определения неприводимых представлений группы достаточно знать след (равный сумме диагональных элементов) матриц, представляющих операции симметрии. В теории групп след матриц представлений часто называют характером. Для всех представлений и операций группы они сведены в таблицу характеров. Пример одной из наиболее часто употребляемых групп, С_2v, приведен ниже.

C2v	E	C2	v(x,z)	'v(yz)
A1 A2 B1 B2	1 1 1 1	1 1 -1 -1	1 -1 1 -1	1 -1 -1 1

Такие таблицы составлены для всех точечных групп и будут в рамках данного курса использоваться без вывода. В этих таблицах +1 означает симметричность (неизменность) свойства функций базисного набора представления при осуществлении операции симметрии, а –1 – антисимметричность. Операции антисимметрии преобразуют предметы, обладающие двумя возможными значениями какого-либо свойства, так, что одно значение переходит в другое. Пример: знак функции.

Важным свойством характеров неприводимых представлений является то, что таблица их умножения соответствует таблице умножения групп.

Ниже приведены таблицы характеров наиболее часто встречающихся групп симметрии.

С2	Е	С2
А В	1 1	1 -1

Сi	Е	i
Аg Au	1 1	1 -1

Сs	Е	
А' A"	1 1	1 -1

С2h	Е	С2	h	i
Аg Вg Au Bu	1 1 1 1	1 -1 1 -1	1 -1 -1 1	1 1 -1 -1

D2	Е	С2(z)	C2(y)	C2(x)
А1 В3 В1 B2	1 1 1 1	1 -1 1 -1	1 -1 -1 1	1 1 -1 -1

С3v	Е	2С3	3h
А1 A2 E	1 1 2	1 1 -1	1 -1 0

D3	Е	2С3	3C21
А1 A2 E	1 1 2	1 1 -1	1 -1 0

C4v	Е	С2	2C4	2v	2'v
А1 A2 B1 B2 E	1 1 1 1 2	1 1 1 1 -2	1 1 -1 -1 0	1 -1 1 -1 0	1 -1 -1 1 0

D4	Е	С2	2C4	2C'2	2C"2
А1 A2 B1 B2 E	1 1 1 1 2	1 1 1 1 -2	1 1 -1 -1 0	1 -1 1 -1 0	1 -1 -1 1 0

D2d	Е	С2	2S4	2C'2	2d
А1 A2 B1 B2 E	1 1 1 1 2	1 1 1 1 -2	1 1 -1 -1 0	1 -1 1 -1 0	1 -1 -1 1 0

C5v	Е	2С5	2C52	5v
А1 A2 E1 E2	1 1 2 2	1 1 2cosx 2cos2x	1 1 2cos2x 2cos4x	1 -1 0 0 x = 2/5

C6v	Е	С2	2C3	2C6	3v	3'v
А1 A2 B2 B1 E1 E2	1 1 1 1 2 2	1 1 -1 -1 -2 2	1 1 1 1 -1 -1	1 1 -1 -1 1 -1	1 -1 1 -1 0 0	1 -1 -1 1 0 0

D3h	Е	h	2C3	2S3	3C'2	3'v
А'1 A'2 A"1 A"2 E" E'	1 1 1 1 2 2	1 1 -1 -1 -2 2	1 1 1 1 -1 -1	1 1 -1 -1 1 -1	1 -1 1 -1 0 0	1 -1 -1 1 0 0

Td	Е	8С3	3C2	6d	6S4
А1 A2 E T1 T2	1 1 2 3 3	1 1 -1 0 0	1 1 2 -1 -1	1 -1 0 -1 1	1 -1 0 1 -1

В теории групп вводится еще одно полезное для химии понятие: понятие о прямом произведении.

Пусть Г₁ – n₁-мерное, а Г₂ – n₂-мерное представления группы G. Тогда матрицы размера (n₁n₂) x (n₁n₂), получаемые как прямые произведения матриц из Г₁ и Г₂, образуют n₁n₂-мерное представление группы G, так называемое прямое (кронекеровское) произведение .

Прямое произведение матрицыразмераm x n и матрицы размераm' x n' есть матрица

(1.46)

размера mm' x nn', где индекс j означает порядковый номер пары (i,i') в последовательности (1,1), (1,2), … , (1,m'), (2,1), (2,2), … , (m,m'), а индекс h – порядковый номер пары (k,k') в аналогичной последовательности.

Характер представленияравен произведению характерапредставленияи характерапредставления:

(1.47)

В качестве примера рассмотрим прямые произведения характеров неприводимых представлений в группе С_3v.

С3v	Е	2С3	3h
А1 A2 E	1 1 2	1 1 -1	1 -1 0

	11		11		-11		=
		21 21 22 11 11		-11 -11 -1(-1) 11 11		01 0(-1) 00 11 (-1)(-1)		= = =

Для того, чтобы закончить с описанием начал теории представлений, покажем два полезных приема: определение состава приводимого представления (разложения его на неприводимые) и использование операторов проектирования.

Разложение приводимого представления на неприводимые.

Можно показать, что разложение любого приводимого представления осуществляется единственным образом, причем число вхождений неприводимого представления i в приводимое представление Г, определяется по формуле:

(1.48)

Здесь a_i –сколько раз i-ое неприводимое представление встречается в приводимом представлении, h – число элементов группы G; R – оператор симметрии группы; - характер операцииR в приводимом представлении; - характер операцииR в i-том неприводимом представлении.

Характер приводимого представления в точечной группе определяется как число элементов базисного набора (представления) группы, которые остаются неподвижными при операции симметрии.

Рассмотрим систему точек 1 … 4.

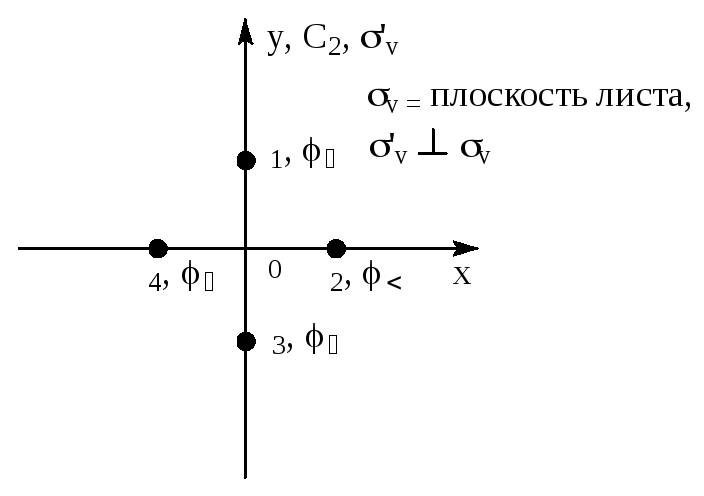
C2V	E	C2(y)	Vпл.	Vпл.(y)
A1	1	1	1	1
A2	1	1	-1	-1
B1	1	-1	1	-1
B2	1	-1	-1	1
	4	2	4	2

Тогда

Отсюда, структуру приводимого представления можно записать как

Последняя запись означает, что в базисный набор функций приводимого представления входят 3 функции, преобразующиеся по представлению А₁ и одна – по представлению В₁.

Часто при применении теории групп для решения физических и химических задач используют метод операторов проектирования. Он позволяет преобразовать произвольный базис таким образом, чтобы он принадлежал к определенному неприводимому представлению группы симметрии. По определению, базис имеет вид:

Здесь h – число элементов симметрии в группе; i – неприводимое представление группы; - операция группы;- характер операциивi-том неприводимом представлении.

Пусть _i – волновая функция атома в точке i:

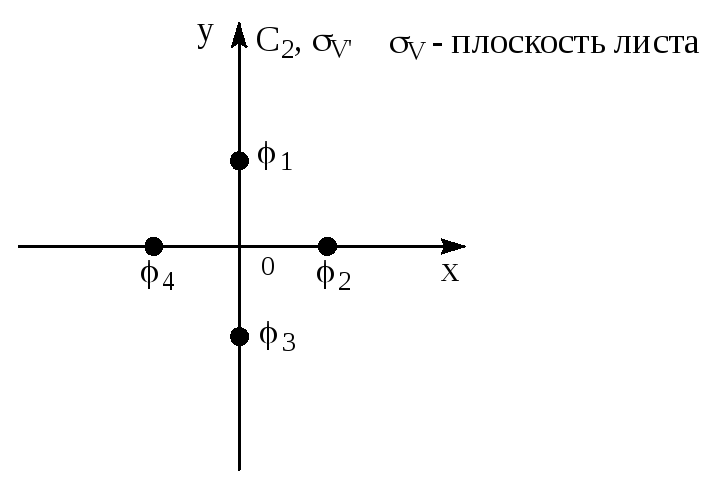
Рис.2

C2V	E	C2	V	V '
A1	1	1	1	1
A2	1	1	-1	-1
B1	1	-1	1	-1
B2	1	-1	-1	1

Тогда волновые функции системы атомов 1-4, удовлетворяющие группе С_2V, будут находиться следующим образом.

Представление А₁:

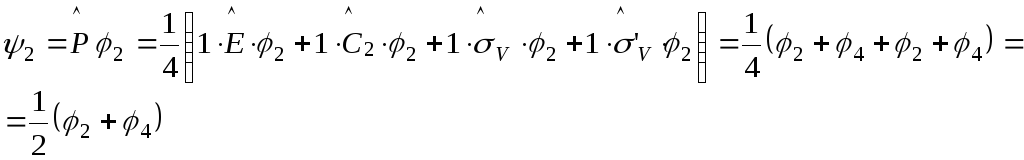
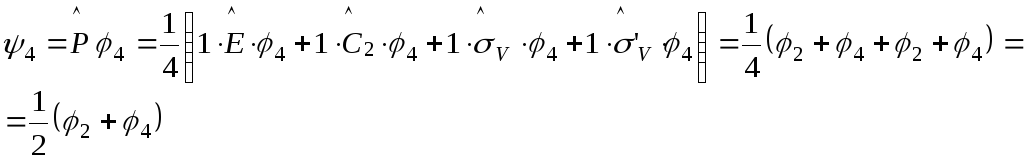
Таким образом ₄ = ₂, т.е. всего образовано 3 волновых функции, преобразующиеся по представлению А₁ группы С_2V.

Представление В₁.