1.5. Элементы теории групп

1.5.1. Понятие о группе (симметрии)

Из эксперимента известно, что большинство химических молекул обладают высокой симметрией, а изолированные атомы – сферической симметрией. Хотя часто нельзя получить точное решение уравнения Шредингера, можно получить некоторые представления о его виде, рассматривая свойства симметрии волновых функций. Очевидно, что волновая функция должна обладать теми же свойствами симметрии, что и молекула или атом, которые она описывает; последнее является следствием инвариантности энергии относительно преобразований симметрии. В частности, симметрию можно использовать для классификации волновых функций.

Наиболее полезна для изучения симметрии теория групп. Остановимся на некоторых ее компонентах.

Набор объектов (например, операторов) образует группу, если они удовлетворяют следующим условиям:

(1) Если элементы ипринадлежат группе, то принадлежит группе и произведение.

(2) Для трех элементов , принадлежащих группе, справедлив ассоциативный закон умножения, т.е. .

(3) Для любого элемента , принадлежащего группе, существует обратный элемент, который также принадлежит группе.

(4) Единичный элемент также принадлежит группе.

Для химических приближений важно заметить, что операции симметрии молекул образуют группу.

Рассмотрим для примера точки 1, 2, 3, 4 на осях координат (в этих точках могут располагаться, например, одинаковые атомы).

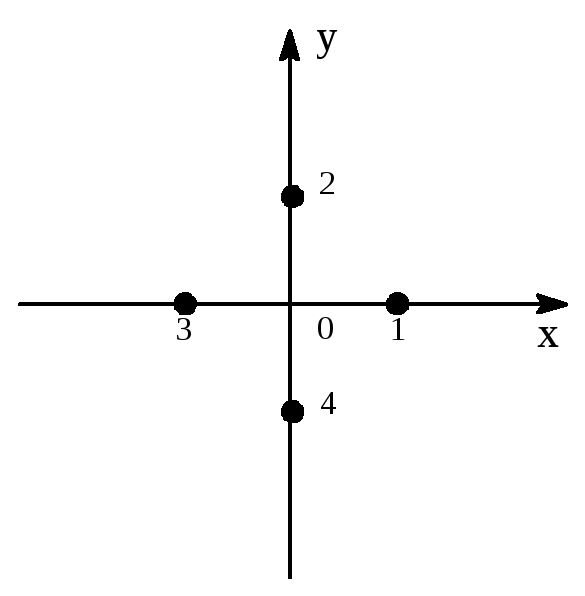
Расположение этих точек обладает высокой симметрией. Применение операций симметрии оставляет без изменения все или некоторые из этих точек.

Взаимные переходы точек при операциях симметрии можно отобразить несколькими способами.

1. При помощи матриц.

Положим, что матричный элемент a_ij = 1, если точка j переходит под действием операции симметрии в точку i, и a_ij = 0, если этого не происходит. Пусть Е – элемент идентичности; С_4h – вращение на 90 в плоскости, перпендикулярной плоскости xОy; С_2V(x) – поворот на 180 вокруг оси Ох; С_i – отражение в центре координат. Тогда

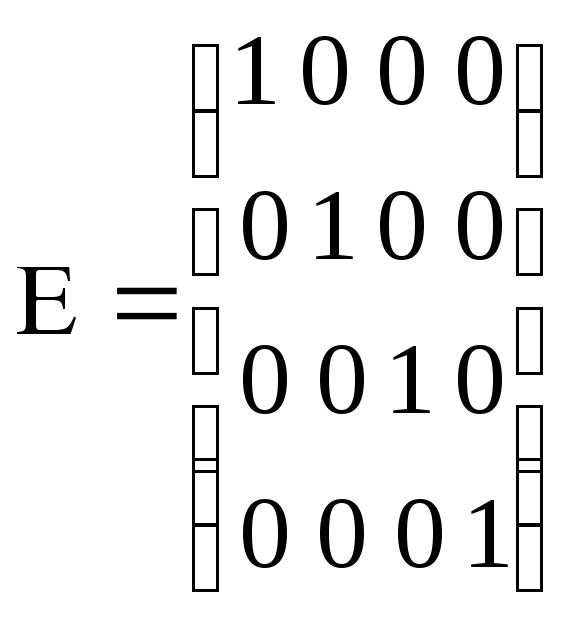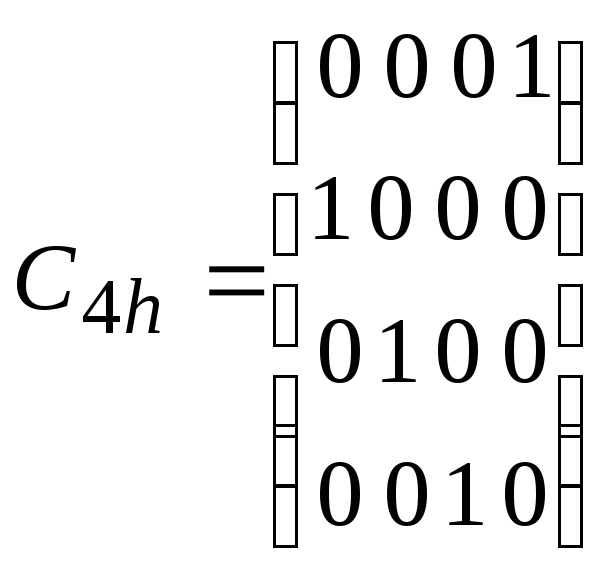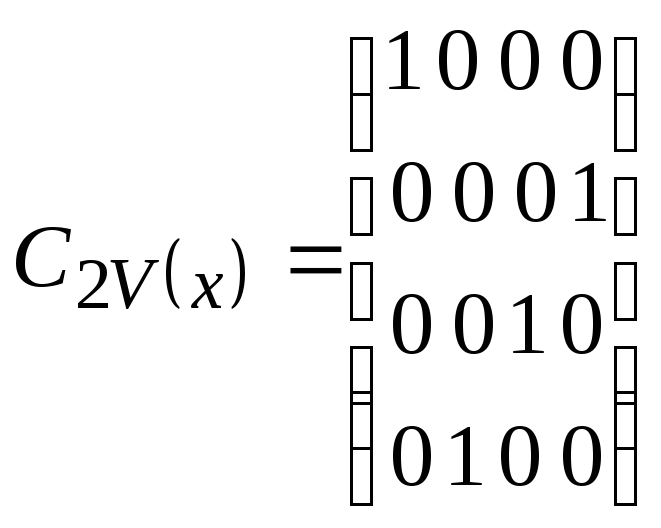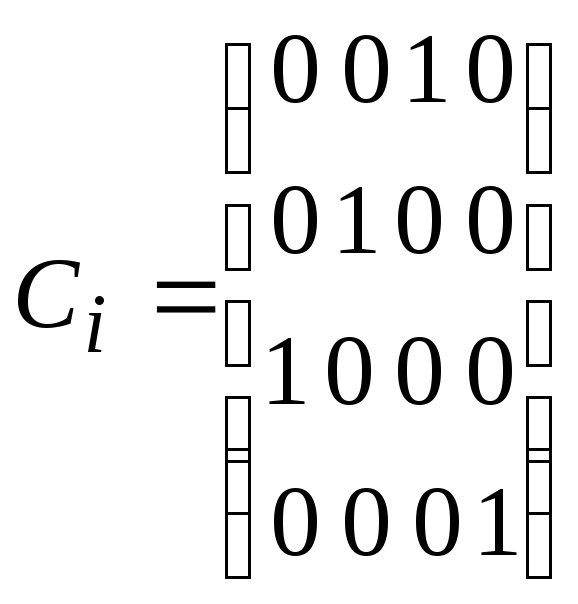; ;;и т.п.

2. При помощи перестановок.

; ;;

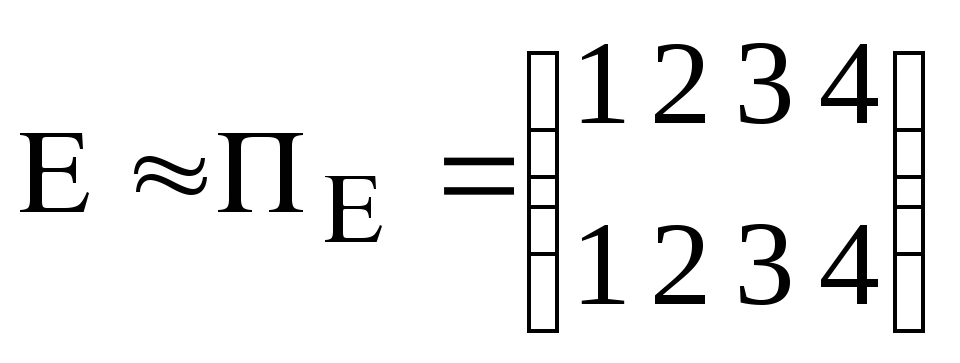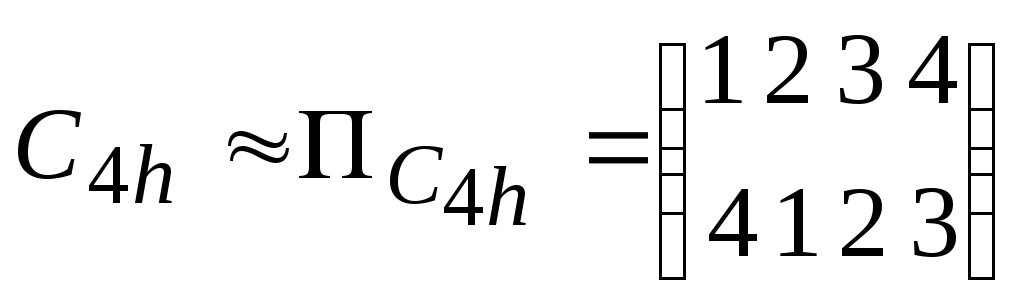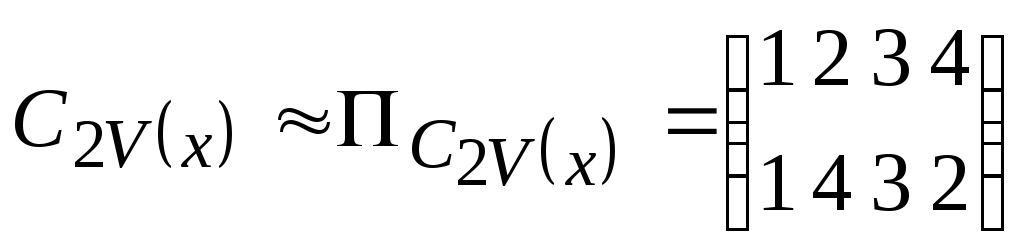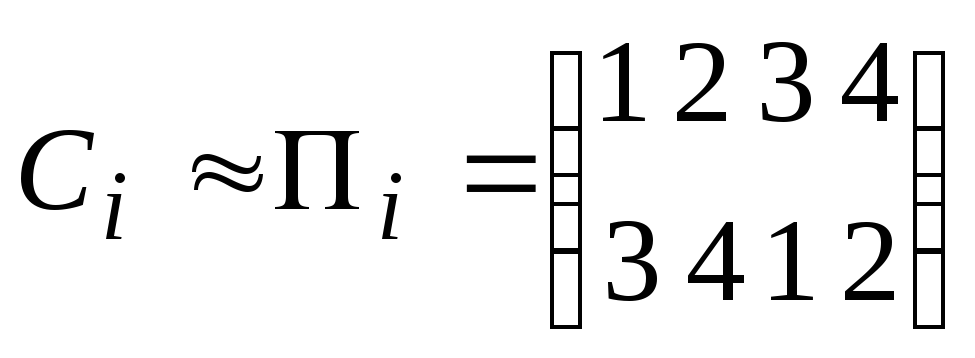и т.п.

Вообще говоря, существует бесконечноемножество способов такого отображения. Однако все они обладают общим свойством: подчиняются групповым постулатам (1) - (4), и, следовательно, образуют группу.

Набор матриц, характеризующий описанные выше переходы точек (объектов) при преобразованиях симметрии, называют представлением группы. Точки (объекты), на которые они действуют – базисными функциями представления.

Выберем в качестве "базисных функций" 8 точек:

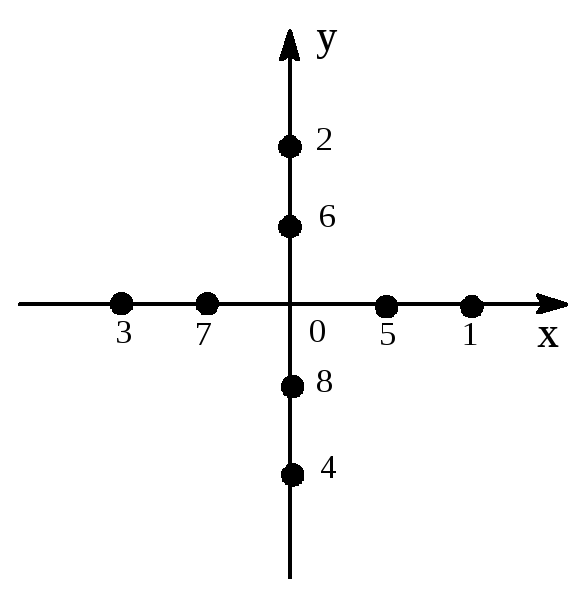
Теперь размерность матриц, представляющих операции симметрии в этой системе, будет 8 х 8. Но эти матрицы будут удовлетворять тем же правилам умножения, что и описанные ранее.

Заметим, что не найдется операции симметрии, результатом действия которой было бы смешение точек 1-4 и 5-8. Матрицы полученного представления можно представить в виде двух блоков.

;;;.

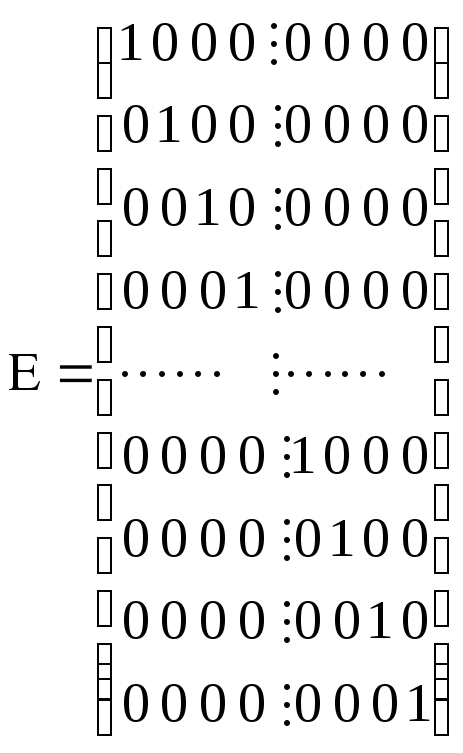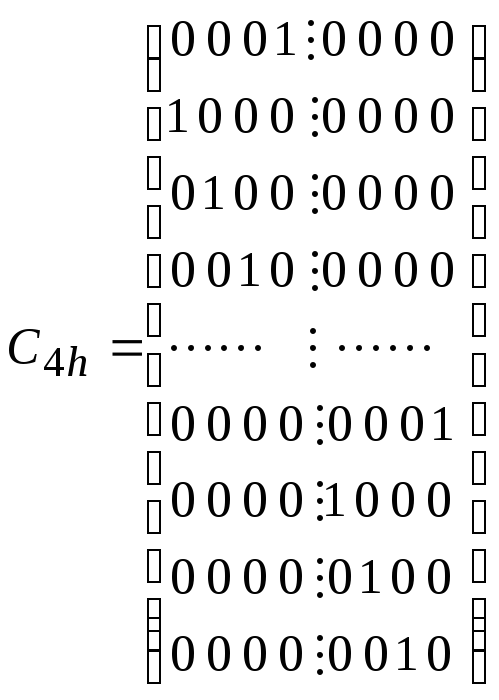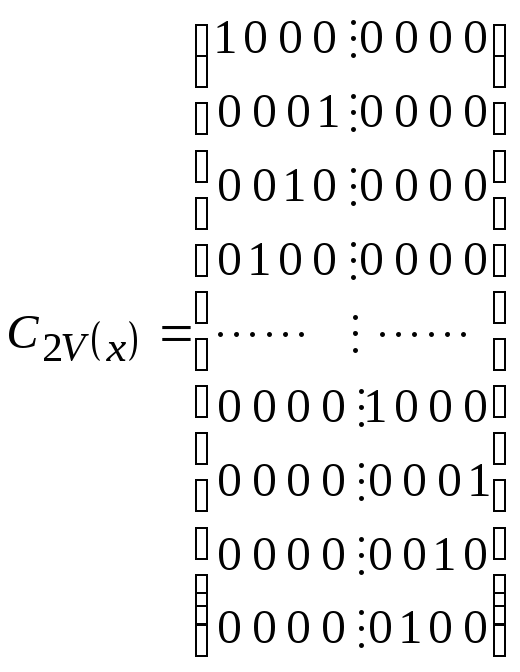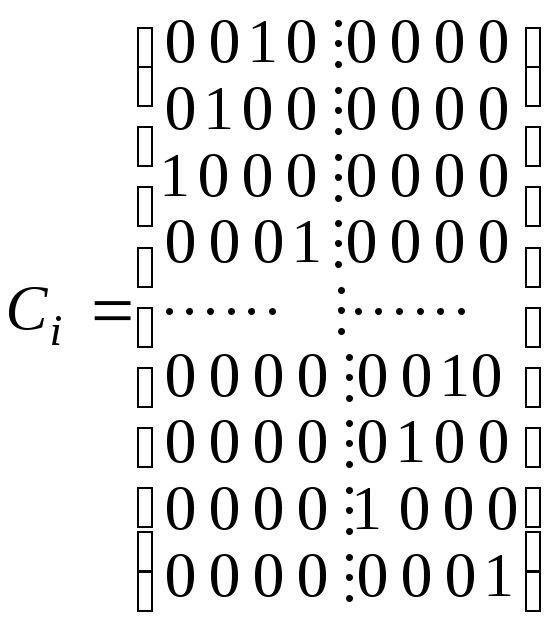Иначе говоря, все эти матрицы можно представить в виде

,

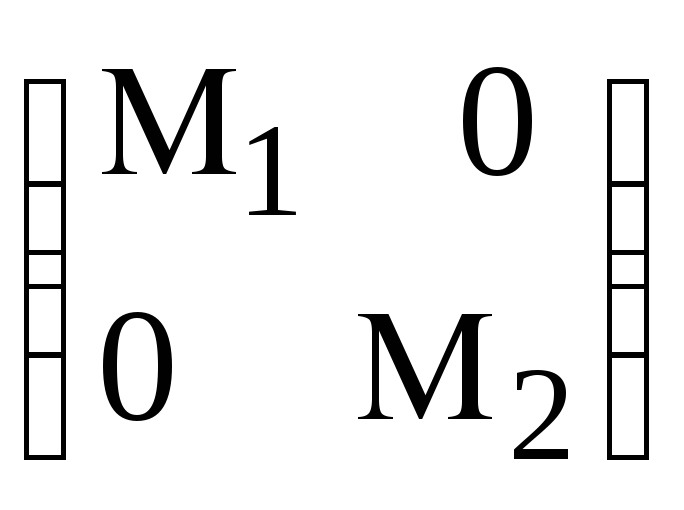причем М₁ действует только на точки 1-4, а М₂ – только на 5-8. Более того, по виду блоки М₁ и М₂ будут теми же.

С точки зрения математики, такое разбиение матриц большей размерности на блочные матрицы с блоками меньшей размерности называется редукцией или приведением. Обычно представление обозначают греческой буквой . Описанная выше редукция будет иметь вид.

Вместо точек можно было бы взять какие-то функции, например, волновые функции одинаковых атомов. Полученные результаты будут теми же. Указанные функции также будут базисными функциями. Важно заметить, что и точки и функции одной и той же симметрии будут образовывать базисные наборы для представления групп симметрии.

Зададимся вопросом: можно ли еще более упростить (привести) матрицу размерности 4 х 4?

Рассмотрим комбинации (Р₁+Р₂+Р₃+Р₄), (Р₁+Р₃-Р₂-Р₄), (Р₃-Р₁) и (Р₄+Р₂). Можно заметить, что при действии операций симметрии первые две суммы остаются неизменными или просто умножаются на –1 (симметрия и антисимметрия). Третья и четвертая комбинации смешиваются, но только друг с другом. Таким образом, они образуют базис для 3-х представлений, первые две – для одномерных , две последних – для двухмерного. Тогда

Дальнейшее разложение или редукция для невозможны; такие представления называютсянеприводимыми в отличие от исходных представлений , которые называютсяприводимыми.

Согласно Малликену существуют следующие правила для обозначения неприводимых представлений.

1. Размерность представления отображается в его имени:

А или В – одномерные представления;

Е – двухмерное представление;

Т – трехмерное представление;

U – четырехмерное представление.

2. Буква А означает, что представление симметрично при операции вращения вокруг главной оси группы симметрии, а В – антисимметрично.

3. Если есть центр симметрии, то добавляется подстрочный индекс "g", если его нет – "u".

4. Индексы 1 и 2 для неприводимых представлений А и В соответствуют симметричному (1) и антисимметричному (2) поведению относительно оси С₂, перпендикулярной главной оси, а при ее отсутствии -_V.

5. Надстрочные индексы ' и " указывают симметричное (') или антисимметричное (") неприводимое представление по отношению к _h.