2.3. Матричное представление операторов. Основные свойства матриц.

Согласно последней из рассмотренных нами теорем, любую функцию можно разложить по полному набору эрмитова оператора , если эта функция определена в той же самой области переменных, что и оператор, и удовлетворяет тем же самым граничным условиям, что оператор, т.е.

(1.12)

где

(1.13)

Иначе говоря, задав полный набор значений С₁, С₂, ...С_n, мы зададим функцию (х) в -представлении.

Пусть теперь оператор переводит функцию, заданную в- представлении равенством:

(1.14)

в функцию

(1.15)

Тогда

Умножив начальный и конечный член этой цепочки равенств на , проинтегрировав пох и приняв во внимание, что функции ортонормированы, т.е.

,

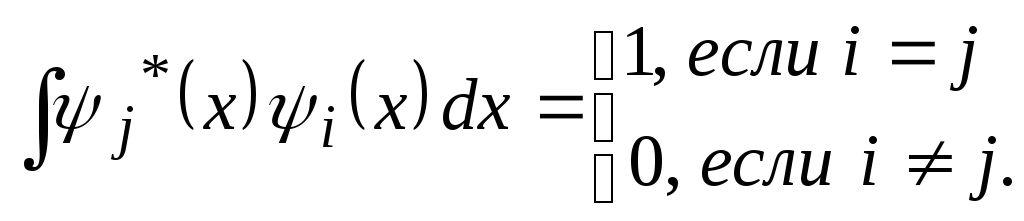получим

т.е.

Набор всех величин есть представление операторав- представлении или, иначе говоря, - представление операторав наборе базисных функций- представления.

Совокупность величин , характеризующих оператор, записывают в виде таблицы, которую называютматрицей:

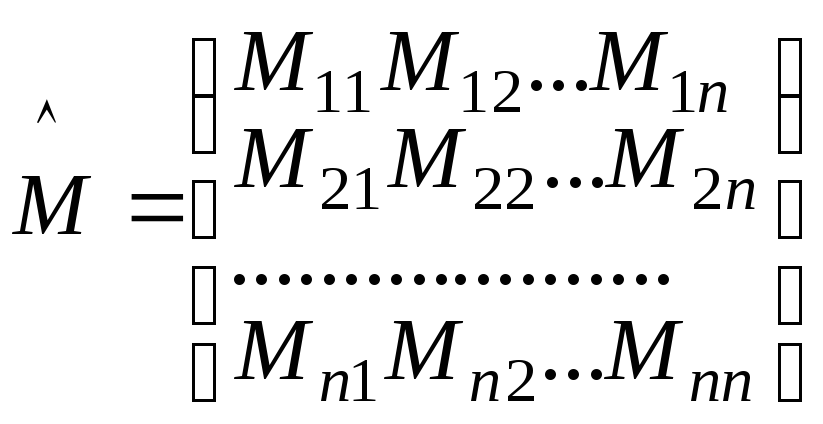(1.16)

Величины называютсяматричными элементами.

Можно (не совсем строго) утверждать следующее: если оператор имеет конечное число собственных значений, его всегда можно представить в виде матрицы.

Остановимся на свойствах матриц.

1. Матрицы равны тогда и только тогда, когда равны их соответствующие матричные элементы, т.е.

^{если (1.17)}

2. Суммой двух матриц называется матрица, матричными элементами которой являются суммы соответствующих матричных элементов слагаемых, т.е.

, ^если .^(1.18)

3. Произведением двух матриц называется матрица, матричные элементы которой определяются по правилу:

(1.19)

т.е. ,

если

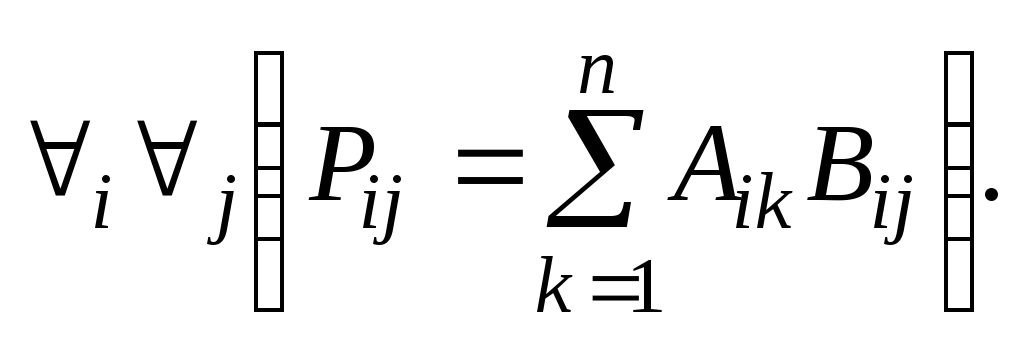(1.20)

4. Возвратимся к задаче на собственные значения оператора

. (1.21)

Разложим функцию  по полному ортонормированному набору:

(1.22)

Принимая во внимание (1.10), имеем

(1.23)

Умножив равенство (1.23) слева на и проинтегрировав пох, имеем

или

, ^{m = 1, …, n (1.24)}

n сумм вида (1.24) эквивалентно системе алгебраических уравнений:

(1.25)

Система уравнений (1.25) является системой n линейных однородных уравнений с n неизвестными. Из алгебры известно, что она имеет решение тогда и только тогда, когда определитель из коэффициентов при неизвестных С₁,С₂,...,С_n равен нулю, т.е.

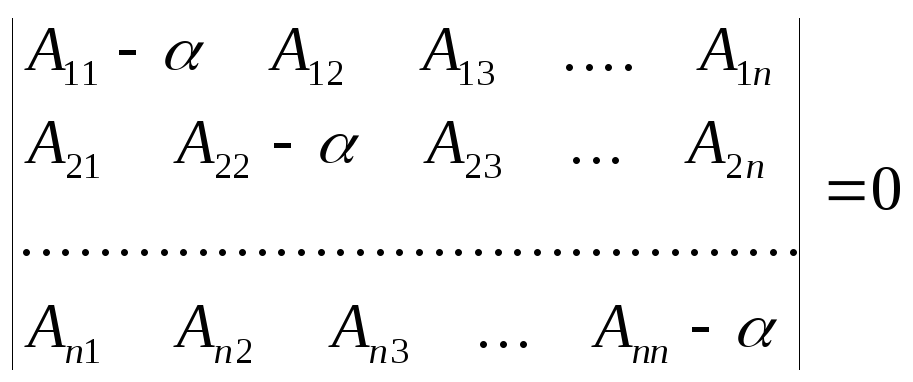(1.26)

Такой определитель называется секулярным или вековым.

Таким образом, если оператор имеет дискретный спектр, то его можно представить в виде матрицы, и задача на собственные значения сведется к задаче на решение системы однородных алгебраических уравнений.

3. Основные постулаты квантовой механики.

Квантовую механику можно построить, если исходить из некоторых общих положений, - постулатов. Они принимаются без доказательств. Справедливость их доказывает соответствие эксперименту результатов, которые можно предсказать с помощью теории, основанной на постулатах.

Постулат 1.

Каждой переменной в уравнениях классической механики соответствует эрмитов оператор в квантовой механике.

Этот постулат называют принципом соответствия. Если его конкретизировать, то

1) координаты и время остаются без изменения;

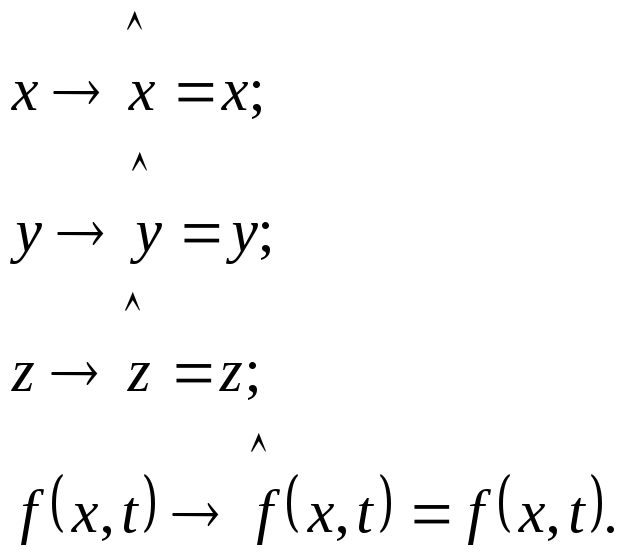(1.27)

2) проекции импульса на координатные оси заменяются на соответствующие операторы:

(1.28)

(1.29)

1.30)

3) а сам импульс - на оператор импульса:

(1.31)

Постулат 2.

Каждое состояние системы частиц полностью описывается функцией координат и времени, называемой волновой функцией

Ее интерпретируют следующим образом (Борн):

выражение есть вероятность того, что переменныеx,y,z в момент времени t находятся в следующем интервале значений:

для частицы 1:

для частицы 2:

и т.д., причем в случае n частиц:

Волновая функция должна удовлетворять следующим свойствам.

1. Быть нормированной,

(1.32)

Это равенство означает, что вероятность найти каждую из n частиц в пространстве в любой момент времени t равна 1.

2. Существовать во всем интервале переменных.

3. Быть непрерывной и конечной во всем интервале существования.

4. Быть однозначной.

Постулат 3.

Волновая функция удовлетворяет уравнению:

(1.33)

Здесь - оператор Гамильтона,t - время, причем

в случае стационарного решения, когда .

Постулат 4.

Единственными значениями, которые можно определить при помощи измерения наблюдаемой величины М, являются собственные значения соответствующего квантово-механического оператора

, (1.34)

т.е. набор чисел m_k.

Постулат 5.

Если рассматриваемая система находится в состоянии, описываемом волновой функцией , то среднее значениенаблюдаемой величиныМ дается выражением:

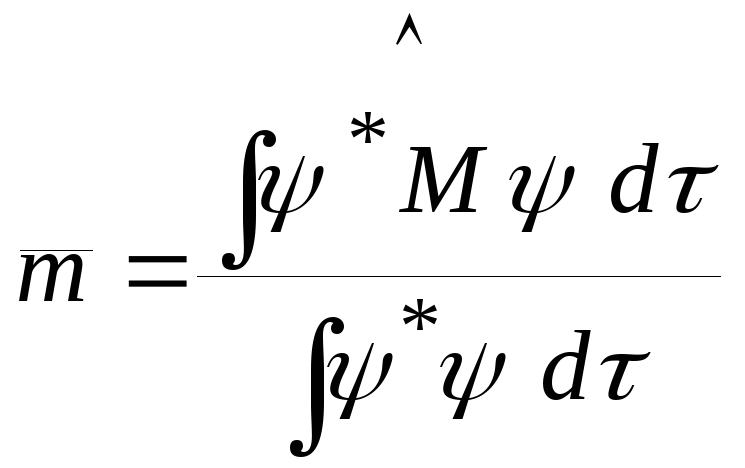(1.35)

Важным следствием последнего постулата является следующее утверждение:

Если система находится в состоянии, описываемом волновой функцией , и волновую функцию можно представить в виде линейной комбинации, то величинаозначает вероятность того, что в момент измерения для наблюдаемой величиныМ будет получено значение m_i, отвечающее собственной функции .