2. Основные законы гидродинамики
2.1Уравнение д. Бернулли с учетом потерь энергии
При установившемся, плавноизменяющемся движении потока реальной жидкости уравнение Бернулли для двух сечений будет иметь следующий вид:
![]() (ІІ
– 1)
(ІІ
– 1)
где V1 и V2 – средние скорости движения в сечениях;
![]() коэффициент
кинетической энергии, принимаемой при
турбулентном режиме движения равным
1,0 – 1,1, а при ламинарном
коэффициент
кинетической энергии, принимаемой при
турбулентном режиме движения равным
1,0 – 1,1, а при ламинарном
![]() (в круглой трубе);
(в круглой трубе);
![]() -
потери удельной энергии на преодоление
сил сопротивления движению потока на
участке между сечениями. Различают два
вида потерь энергии: по длине и на
преодоление местных сопротивлений. В
общем случае
-
потери удельной энергии на преодоление
сил сопротивления движению потока на
участке между сечениями. Различают два
вида потерь энергии: по длине и на
преодоление местных сопротивлений. В
общем случае
![]() (ІІ
– 2)
(ІІ
– 2)
где hl- потери энергии по длине;
![]() сумма
потерь энергии на преодоление местных
сопротивлений.
сумма
потерь энергии на преодоление местных
сопротивлений.
Оба вида потерь энергии определяется по такой зависимости:
![]() , (ІІ
– 3)
, (ІІ
– 3)
где
![]() -
коэффициент потерь
-
коэффициент потерь
При учете потерь энергии по длине в трубопроводах, коэффициент потерь определяется так:
![]() , (ІІ-
4)
, (ІІ-
4)
где
![]() - гидравлический коэффициент трения
(коэффициент Дарси);
- гидравлический коэффициент трения
(коэффициент Дарси);
l – длина участка трубопровода, на котором определяются потери энергии;
d – диаметр трубопровода.
При ламинарном режиме коэффициент трения зависит только от числа Рейнольдса и для труб круглого сечения определяется по формуле
![]()
(ІІ- 5)
При турбулентном режиме могут быть выделены три области гидравлических сопротивлений.
Область
гладких русел
для труб при числах Рейнольдса 2320 < Re
< 10![]()
Где d – диаметр трубопровода;
![]() - эквивалентная
шероховатость.
- эквивалентная
шероховатость.
В этой области
гидравлических сопротивлений коэффициент
трения![]() зависит только Рейнольдса и может быть
определен по формуле Блазиуса:
зависит только Рейнольдса и может быть
определен по формуле Блазиуса:
![]() . (ІІ-
6)
. (ІІ-
6)
Переходная область наблюдается при числах Рейнольса
![]() .
.
В этом случае для определения коэффициента трения может быть рекомендована формула А.Д. Альтшуля
![]()
(ІІ- 7)
Как видно из зависимости (ІІ – 7), в переходной области гидравлических сопротивлений коэффициент трения зависит и от числа Рейнольдса и от шероховатости трубы.
Квадратичная
область
гидравлических сопротивлений наступает
при Re > 560![]() .
.
В этой области коэффициент трения не зависит от числа Рейнольдса и может быть определён по формуле Шифринсона:
![]() .
(ІІ- 13)
.
(ІІ- 13)
В этой же области гидравлических сопротивлений для стальных и чугунных труб, бывших в употреблении, может быть рекомендована формула Ф. А. Шевелёва
![]() (ІІ-
14)
(ІІ-
14)
Величина
эквивалентной шероховатости
![]() зависит от материала, способа изготовления
и соединения труб, от продолжительности
эксплуатации.
зависит от материала, способа изготовления
и соединения труб, от продолжительности
эксплуатации.
Расход жидкости, протекающей по трубопроводу, вычисляется по формуле
![]() Ωрасч
Ωрасч![]() .
.
При расчёте гидравлически длинных трубопроводов, работающих в квадратичной области сопротивления, расход можно определить по формуле
![]() ,
(43)
,
(43)
где J – гидравлический уклон потока
![]() ;
(44)
;
(44)
K – модуль расхода
K=
Ω![]() ,
(45)
,
(45)
R
– гидравлический радиус (R
=
![]() ).
).
Из формул (43) и (44) потеря напора hl выражается зависимостью
![]() .
.![]()
![]() (46)
(46)
Задачи:
№ 3.1
|
На берегу реки предполагается устроить насосную станцию для подачи воды из реки расходом Q. Высота оси насоса над уровнем воды в реке hн. Длина всасывающей трубы l, |
|
допустимая скорость
v,
трубы чугунные новые. Температура воды
![]() ,
,![]() .
.
1. Определить диаметр всасывающей трубы.
2. Определить величину наибольшего вакуума.
|
Исходные данные |
Номер варианта | |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
l, м Q,м3/с v, м/с |
4,0 0,5 20 0,02 0,8 |
5,0 0,4 25 0,03 0,9 |
3,0 0,3 30 0,04 0,75 |
2,0 0,35 15 0.02 0,7 |
4.5 0.3 10 0,035 0,8 |
3,5 0,4 35 0.03 0,7 |
2,5 0,3 27 0,025 0,85 |
5,5 0,5 32 0,045 0,95 |
6,0 0,5 37 0,05 0,08 |
6,5 0,4 27 0,06 0,09 |
№ 3.2
|
Определить
напор H,
необходимый для пропуска расхода воды
Q
через систему труб. Диаметры труб
|
|
|
Исходные данные |
Номер варианта | |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
Q,м3/с
|
0,05 40 32 50 50 40 30
|
0,1 80 50 100 70 80 90
|
0.15 125 90 175 75 45 80
|
0.06 50 40 75 80 60 100
|
0.12 90 75 125 100 90 60
|
0.08 75 40 80 125 100 70
|
0,14 100 75 125 70 80 100
|
0.09 75 50 90 40 70 50
|
0.07 50 25 75 90 80 40
|
0.04 32 25 40 100 50 60
|
№ 3. 3
|
Определит
потери напора при подаче воды со
скоростью v,
при температуре
|
|
Исходные данные |
Номер варианта | |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
v, м/с d, мм l, м |
0,13 200 1500 |
0,18 150 1000 |
0,10 100 1200 |
0,22 125 1700 |
0,15 80 900 |
0,2 100 2000 |
0,25 150 2400 |
0,3 200 1800 |
0,28 150 1400 |
0,26 125 1600 |
№ 3.4
|
Определить
потери давления при движении воды в
стальном трубопроводе диаметром d,
длиной L,
который состоит из секций длиной
l=10м,
сваренных электродуговой сваркой с
толщиной выступа стыка над внутренней
поверхностью трубопровода |
|
Исходные данные |
Номер варианта | |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
d,мм L, м Q, t,
|
100 200 0,05 20
|
150 250 0,1 15
|
125 180 0,08 30
|
175 300 0,15 40
|
90 160 0,06 60
|
80 150 0.04 80
|
100 220 0,07 10
|
75 130 0,11 20
|
50 100 0,09 50
|
125 180 0,14 60
|
№ 3.5
|
По трубопроводу постоянного поперечного сечения перекачивается жидкость плотностью 950кг/м3. Избыточное давление в начале трубопровода равно PM . Пренебрегая потерями напора при движении жидкости, определить максимальный угол наклона трубопровода к горизонту, чтобы давление в конце трубопровода было равно атмосферному, если длина трубопровода l. |
|
Исходные данные |
Номер варианта | |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
PM, МПа l,км
|
300 5
|
250 4,5
|
400 4
|
350 3
|
280 3.5
|
320 2,5
|
430 5.5
|
360 3,8
|
395 2,9
|
270 3,6
|
№ 3.6
|
Определить
потери напора в водопроводе длиной l
при подаче Q,
если трубы чугунные, бывшие в эксплуатации
с диаметром d.
Температура воды
|
|
Исходные данные |
Номер варианта | |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
l, м Q, d, мм
|
500 0,1 250
|
700 0,04 200
|
550 0,08 175
|
450 0,12 150
|
600 0,15 125
|
400 0,14 200
|
650 0,06 100
|
750 0,16 250
|
800 0,2 225
|
600 0,18 200
|
№ 3.7
|
Определить расход воды Q в трубе диаметром d1, имеющей плавное сужение до диаметра d2, если показания пьезометров до сужения h1, в сужении h2. Температура
воды
|
|
Исходные данные |
Номер варианта | |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
|
250 125 50 30
|
150 80 120 40
|
100 50 150 50
|
80 40 90 20
|
200 50 105 20
|
90 50 100 40
|
75 40 65 30
|
200 100 110 30
|
50 25 60 20
|
40 15 55 1
|
№ 3.8
|
Определить
потерю напора в трубопроводе длиной
l
и диаметром D
при перекачке нефти плотностью
|
|
Исходные данные |
Номер варианта | |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
l, м D, мм Q, л/с
|
500 200 25 |
1000 150 20 |
750 125 15 |
930 250 30 |
600 90 14 |
800 300 40 |
640 150 25 |
870 175 30 |
900 200 50 |
550 250 60 |
№ 3.9
|
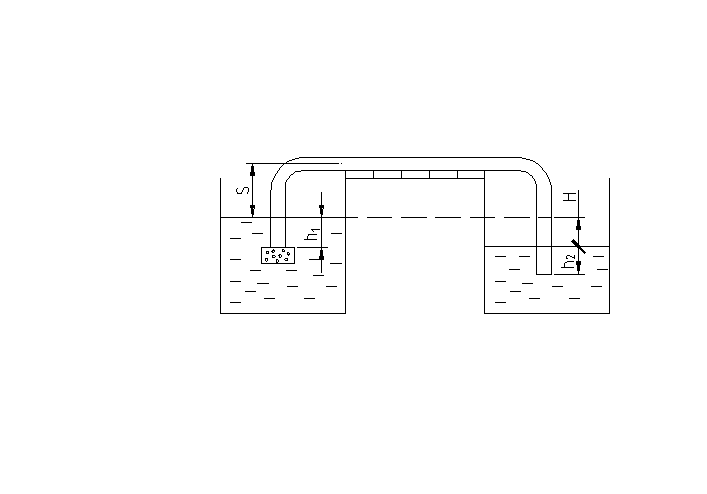
Определить какой расход можно перекачать сифоном из водоема А в водоем В, определить разность горизонтов в водоемах Н, если длина сифона l, диаметр сифона d, скорость воды в сифоне v. |
|
Температура воды
![]() .
Трубы чугунные, нормальные (
.
Трубы чугунные, нормальные (![]() )
)
|
Исходные данные |
Номер варианта | |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
l, м d, мм v, м/с
|
75 200 1,1
|
90 150 0,9
|
100 175 1.0
|
120 125 0,7
|
60 100 0,8
|
40 90 1.2
|
50 80 1,5
|
80 50 1,4
|
130 125 0.9
|
140 150 0.8
|
№ 3.10
Определить потери
напора при подаче воды со скоростью v
через трубку диаметром d
и длиной l
при температуре воды
![]() .
.
|
Исходные данные |
Номер варианта | |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
V, м/с d, мм l, м
|
0,12 20 20
|
0,15 15 30
|
0.2 25 50
|
0,25 32 60
|
0,3 40 55
|
0,4 50 70
|
0,35 60 35
|
0,45 80 75
|
0.5 90 80
|
0.7 100 90
|
№ 3.11
По трубопроводу, соединяющему два резервуара, движется вода расходом Q. Трубы стальные новые. Длина трубы l, ее диаметр D. На трубе имеются местные сопротивления: вход в трубу, два поворота, открытая задвижка и выход из трубы. Приняв, что уровни в резервуарах неизменны, определить разность горизонтов воды в резервуарах.
|
Исходные данные |
Номер варианта | |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
Q, л/с l, м D, мм
|
2.5 150 50
|
3.0 200 75
|
4,0 250 80
|
3.5 100 60
|
2.0 120 40
|
2.7 90 32
|
3.2 180 60
|
4.3 140 50
|
3.8 130 200
|
2.4 110 40
|
№ 3.12
|
Определить
манометрическое давление, которое
должен создать насос, чтобы подать
воду в количестве Q
в водонапорный бак на высоту h
по трубопроводу длиной l.
Диаметр труб
|
|
При расчете
![]() .
Температуру воды принять
.
Температуру воды принять![]() ,=0.29.
,=0.29.
|
Исходные данные |
Номер варианта | |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
Q,3/с h, м l, м
|
0,015 12 50
|
0,02 10 75
|
0.01 8 40
|
0.025 15 70
|
0.03 20 85
|
0.18 18 65
|
0.022 9 35
|
0,033 11 55
|
0.035 22 90
|
0,04 13 60
|
БИБЛИОГРАФИЧЕСКИЙ СПИСОК