Принято использовать коэффициенты χi( j) форм колебаний, которые вводят-

Первая и вторая формы колебаний построены на рис. 8. Из рисунка видно, что первое главное колебание с меньшей частотой k1 = 61,5 рад/с является симметричным (в том смысле, что колеса поворачиваются в разные стороны), причем амплитуда колебаний колеса 2 приблизительно в полтора раза меньше амплитуды колебаний колеса 1. Главное колебание с большей частотой k2 = 93,2 рад/с является антисимметричным, при этом амплитуда колебаний колеса 2 в 1,4 раза меньше амплитуды колебаний колеса 1.

Уравнения (18а), определяющие первое главное колебание, примут вид

ϕ2

Рис. 8

3.4.Закон движения механической системы

Общее решение системы уравнений движения (12б) определяется линейной суперпозицией собственных форм колебаний рассматриваемой механической системы (21а) и (21б):

μ2 = χ(22) при условии, что χ1(1) =1 и χ1(2) =1.

Найдем из начальных условий постоянные интегрирования: амплитуды ко-

Уравнения (22) и (23) справедливы для любого момента времени t. Следовательно, при t = 0:

Подставляя в выражения (25) численные значения входящих в них величин, получаем

С учетом обобщенных возмущающих сил

Из системы уравнений (31) найдем значения углов поворота дисков при статическом действии момента, равного амплитуде возмущающего воздействия (M = M0). При этом sinωt = 1, а ϕ1 = ϕ2 = 0 . В результате получаем

С помощью (37) перепишем уравнение (35) через статические значения углов поворота:

€

ентов инерции M , для коэффициентов динамичности получим

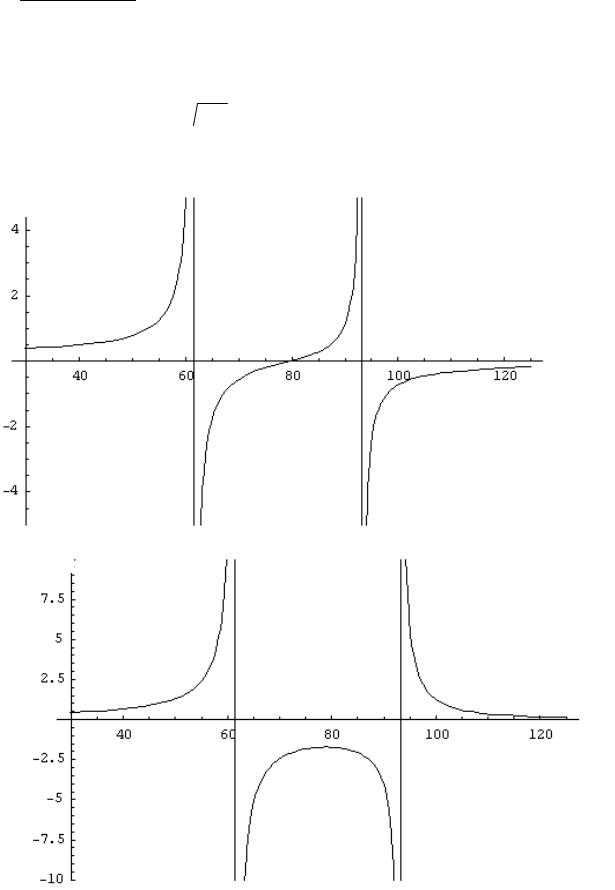
Рассмотрим поведение Φ1(ω) и Φ2(ω) для трех интервалов изменения частоты возмущающего момента: а) 0 ≤ ω< k1; б) k1 < ω< k2 ; в) k2 < ω< ∞ (см.

рис. 9).

а) 0 ≤ ω< 61,5 .

В этом случае знаменатель в формулах (39) положителен. Следовательно, Φ1 > 0 и Φ2 > 0. С ростом частоты ω амплитуды колебаний обоих колес возрастают, причем их колебания происходят в одной фазе с изменением возмущающего момента. При ω = k1 в системе наступает первый резонанс и функции Φ1(ω) и Φ2(ω) претерпевают бесконечный разрыв. При действии момента сил резонансной частоты амплитуды колебаний возрастают пропорционально времени.

28

б) 61,5 < ω<93,2 .

В этом случае знаменатель в формулах (39) отрицателен. Следовательно, на рассматриваемом интервале частот Φ2 < 0, то есть, колебания колеса 2 про-

исходят в противофазе с изменением возмущающего момента.

Для определения знака функции Φ1(ω) нужно рассмотреть числитель форму-

лы (39а). Если k1 < ω< a22 ( 61,5 < ω< 79,3), то Φ1 < 0 и колебания колеса 1, так же как и колеса 2, происходят в противофазе с изменением возмущающего

Φ1

ω, с–1

Φ2

ω, с–1

29

Рис. 9

момента. Если же a22 < ω< k2 ( 79,3 < ω<93,2 ), то Φ1 > 0 и колебания колеса 1 происходят синфазно с изменением M. При ω= a22 = 79,3 с–1, Φ1 = 0.

Вэтом случае колесо 2 можно рассматривать как гаситель колебаний колеса

1.Явление отсутствия вынужденных колебаний колеса при действии на него

возмущающего момента частоты ω= a22 называется антирезонансом, а

само значение частоты – антирезонансной частотой. При ω = k2 = 93,2 в системе наступает второй резонанс.

в) 93,2 < ω< ∞.

В этом случае знаменатель в формулах (39) положителен. Так как k2 > a22 ,

то Φ1 < 0, а Φ2 > 0. С ростом частоты ω амплитуды вынужденных колебаний обоих колес уменьшаются, стремясь к нулю. Колебания колеса 1 происходят в противофазе, а колеса 2 — в одной фазе с изменением возмущающего момента.

30

ЛИТЕРАТУРА

1.Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний.–М: Наука, 1981.

2.Бабаков И.М. Теория колебаний. – М: Наука, 1965.

3.Бидерман В.Л. Теория механических колебаний. – М.: Высш. шк., 1980.

4.Бицено К.Б., Граммель Р. Техническая динамика.–М.: ГИТТЛ, 1952.–Т.2.

5.Бутенин Н.В., Неймарк Ю.И., Фуфаев Н.А. Введение в теорию нелинейных колебаний. – М.: Наука, 1987.

6.Вибрации в технике. Справочник: В 6 т./ Ред. совет: В.Н. Челомей (предс.). – М.: Машиностроение, 1978 – 1982.

7.Вихренко В.С. Линейные колебания в системах с дискретными параметрами. – Минск: БТИ, 1993.

8.Вихренко В.С. Устойчивость и нелинейные колебания.–Минск: БТИ, 1993.

9.Вихренко В.С. Численные методы в теории линейных колебаний. – Минск: БГТУ, 1995.

10.Вихренко В.С. Колебания упругих балок и пластин.– Минск: БГТУ, 1996.

11.Пановко Я.Г. Введение в теорию механических колебаний. – М.: Наука, 1980.

12.Пановко Я.Г., Губанова И.И. Устойчивость и колебания упругих систем.

– М.: Наука, 1979.

13.Потсон Т., Стюарт Н. Теория катастроф и ее приложения.–М.: Мир, 1980.

14.Сборник заданий для курсовых работ по теоретической механике / Под ред. А.А. Яблонского. – М.: Высш. шк., 1985.

15.Тимошенко С.П. Колебания в инженерном деле. – М.: Физматгиз, 1963.

31

32

33