5

УДК 534

Рассмотрены и рекомендованы к изданию редакционно-издательским советом университета.

Составители: В.С. Вихренко, А.В. Кондратенко

Рецензент доцент кафедры лесных машин и технологии лесозаготовок С.П. Мохов

По тематическому плану изданий учебно-методической литературы университета на 2002 год. Поз. 42.

Для студентов специальности 1-36 05 01 «Машины и оборудование лесного комплекса»

©Учреждение образования «Белорусский государственный технологический университет», 2002

©Вихренко В.С., Кондратенко А.В., составление, 2002

6

ВВЕДЕНИЕ

Движение механизмов, машин, манипуляторов и других механических устройств, как правило, сопровождается колебаниями их отдельных частей друг относительно друга, которые привносят в поведение устройств существенные особенности, отличающиеся большим разнообразием. Устойчивость равновесия и движения различных устройств играет важнейшую роль в обеспечении их работоспособности и безопасности эксплуатации. Исследование устойчивости в значительной мере связано с анализом движения при отклонениях от равновесия или от невозмущенного движения. Этот анализ выполняется методами, обычно используемыми в теории колебаний. Поэтому приведенная ниже программа курса «Прикладная теория колебаний» включает в себя и вопросы по устойчивости движения и теории катастроф.

Целью курса является ознакомление студентов с основными особенностями поведения механических систем при наличии колебательных процессов, приобретении ими навыков составления уравнений движения и анализа их решений в отдельных случаях.

В основе теории колебаний лежат сведения из теоретической механики, теории машин и механизмов, сопротивления материалов. В ней широко используются математические методы. Для изучения теории колебаний студентам четвертого курса необходимо вспомнить материал этих фундаментальных и общеинженерных дисциплин, изучавшихся на младших курсах. Поэтому предлагаемый курс следует рассматривать как одно из звеньев непрерывной фундаментальной подготовки студентов, являющейся неотъемлемой частью учебного процесса в университете.

По теории колебаний в 50 – 80-х годах XX столетия было издано огромное количество литературы. В конце пособия приведены ссылки на книги, которые могут быть использованы как при прохождении данного курса, так и для дальнейшего более глубокого изучения теории колебаний и устойчивости движения. Более полный список литературных источников может быть найден в пособиях [6 – 9] и цитируемых в них работах.

Для закрепления полученных знаний предлагается расчетная работа, которую студенты должны выполнить в соответствии со своими индивидуальными вариантами. Порядок выбора вариантов задач указывает преподаватель. Расчетная работа выполняется в ученических тетрадях или на листах формата А4. В каждой задаче приводятся схема, аккуратно выполненная с использованием чертежных принадлежностей или графических редакторов, краткое условие и исходные данные. Решение задач должно сопровождаться пояснениями и необходимыми схемами или рисунками. В пособии даны примеры оформления и методические указания к решению задач. Формулы нумеруются в каждой задаче отдельно. При составлении задач использовался Сборник заданий [14]. Составители выражают благодарность студентам А.Ф. Аникеенко и В.П. Толкачеву за помощь в подготовке рисунков.

7

ПРОГРАММА КУРСА

Фазовые переменные и фазовое пространство механической системы. Фазовые портреты автономных механических систем с одной степенью свободы. Фазовые портреты линейных механических систем и классификация особых точек (центр, фокус, узел, седло). Сепаратрисы. Фазовый портрет физического маятника.

Устойчивость равновесия и движения механических систем. Исследование устойчивости по первому приближению и с помощью функций Ляпунова. Показатели Ляпунова. Теорема Лагранжа – Дирихле. Устойчивость равновесия системы со многими степенями свободы. Критерий Сильвестра.

Элементы теории катастроф. Диаграммы устойчивости и бифуркационные диаграммы стационарных механических систем. Ферма Мизеса. Катастрофы типа сборки и складки.

Нелинейные колебания и методы их исследования. Метод гармонического баланса. Скелетные (каркасные) кривые слабо нелинейных систем с одной степенью свободы. Амплитудно-частотные характеристики. Вынужденные колебания систем с мягкой и жесткой характеристиками. Супер- и субгармонические колебания. Устойчивость колебаний.

Параметрические колебания и параметрический резонанс. Маятник Капицы. Уравнение Матье. Диаграмма Айнса-Стрэтта.

Автоколебания. Метод медленно меняющихся амплитуд. Устойчивый и неустойчивый предельные циклы. Автоколебания в станках.

Собственные колебания системы со многими степенями свободы. Собственные частоты и собственные формы колебаний. Спектр колебаний. Резонанс и антирезонанс. Динамическое гашение колебаний. Самосинхронизация колебаний и ее использование для виброзащиты. Функция Релея и влияние сопротивления на амплитудно-частотные характеристики. Использование диссипации для гашения колебаний. Колебания в станках и механизмах. Методика составления уравнений колебаний многомассовых систем (передаточные механизмы, транспортные машины). Дискретизация уравнений движения упругих тел (многомассовые модели деревьев, хлыстов).

Колебания непрерывных упругих систем. Дифференциальное уравнение поперечных колебаний балки и его интегрирование с помощью функций Крылова. Начальные и граничные условия. Собственные частоты и собственные формы колебаний. Вынужденные поперечные колебания балки. Зависимость амплитуды колебаний от точки приложения вынуждающей силы. Динамические коэффициенты влияния.

Поперечные колебания круглых и прямоугольных пластин. Дифференциальное уравнение поперечных колебаний тонких пластин. Собственные формы колебаний. Зонтичные и веерные колебания. Колебания круглых дисковых пил и их устойчивость.

8

ЗАДАЧА 1

Исследование устойчивости положений равновесия механической системы и построение диаграммы устойчивости

Условие задачи.

Система состоит из нескольких тел и пружин жесткости ci . lio − естественная длина i-й пружины; γ − удельный вес единицы длины стержня или нити; L – длина нити. Заданы веса тел Gi , геометрические параметры и со-

отношение α между жесткостью пружины и весом одного из тел или между весами двух тел. Схемы систем приведены на стр. 9 – 11. Требуется определить положения равновесия ϕe в зависимости от коэффициента α , исследо-

вать их устойчивость и построить диаграмму устойчивости ϕе = ϕе(α) .

Должны быть использованы следующие соотношения между параметрами:

Тип А. c1 = c, c2 = 2c, a = 2l, G1 = G, G2 = 2G, G3 = 4G,

α = cl/G (для четных вариантов) или α = G / cl (для нечетных вариантов).

Тип Б. c1 = 2c, c2 = c, a = 3l, G1 = 2G, G2 = G, G3 = 3G,

α = cl/G (для нечетных вариантов) или α = G / cl (для четных вариантов).

Тип В. c1 = 2c, c2 = 3c, a =1.5l, G1 = 2G, G 2 = 4G, G3 = 3G,

α = cl/G (варианты 1 – 15) или α = G / cl (варианты 16 – 30). Дополнительные условия для вариантов:

1) l10 = l, l20 =1.5l. 2) l0 =l . 3) l0 = 2l . 4) l0 = 2R . 5) 0 ≤ ϕ < π, l0 = 2l . 6) l0 =1.5l . 7) l0 = b . 8) l0 = b . 9) l0 =1.5l . 10) l0 = 3l, G3 = G2 .

11) l10 =1.5l, l20 = 2l . 12) l0 =1.5l . 13) l0 = l . 14) 0 ≤ ϕ < π, l0 = 3l . 15) l0 = 2l . 16) l0 = 4l . 17) l0 = 4l . 18) γ2 = G2 / l , α = G1 / G2 .

19)l10 = 2l, l20 = 2l . 20) l0 = 2R . 21) α = G1 / G2 .

22)L = a + l, b =3l, l0 = 2l . 23) l0 = b − l . 24) l0 = b − l . 25) l0 = l .

26)L = 2.5l, l0 = l . 27) α = G2 / G1. 28) α =G1 / γR . 29) L = 2l, l0 =l .

30)L = 4l, γl = G2 , α = G2 / G1.

Рисунки на стр. 34–36.

Методические указания и пример решения задачи

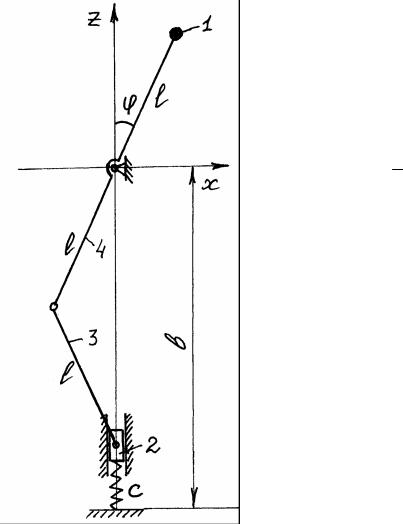
Дано: схема механизма, состоящего из четырех тел и пружины, а также соотношения между его параметрами G1 = 9G, G2 = 2G, γl = 2G,

G = αcl , b = 2l + l0 (см. рис. 1).

Необходимо: найти положения равновесия механизма в зависимости от параметра α и построить диаграмму устойчивости системы.

Решение.

Потенциальная энергия тела в поле сил тяжести

∏ = mgz = Qz,

где m – масса и Q – вес тела; z – вертикальная координата центра тяжести,

9

отсчитываемая от некоторого произвольно выбранного начала отсчета.

∏тяж = ∏1 +∏2 +∏3 +∏4 =

=G1 − 2G2 − 3 γl l cosϕ= 2Gl cosϕ.

2

Потенциальная энергия сил упругости

10

Исследуем положения равновесия на устойчивость. В соответствии с теоремой Лагранжа – Дирихле критерием устойчивости положения равновесия является неравенство

На основании уравнения (3) находим вторую производную потенциальной энергии

Здесь правая часть сформирована так, чтобы в круглых скобках было выделено выражение, составляющее левую часть уравнения (4а). Это упрощает последующий анализ.

Подставляем в уравнение (7) равновесные значения угла ϕ и анализируем знак полученного выражения:

положение равновесия неустойчиво.

Это положение равновесия устойчиво при α < 4.

поскольку при ϕ = ϕ3 выражение в круглых скобках в правой части (7) об-

ращается в нуль (см. уравнение (4a)). Это положение равновесия устойчиво при всех значениях α, при которых оно существует, т.е. при 0 < α < 4 .

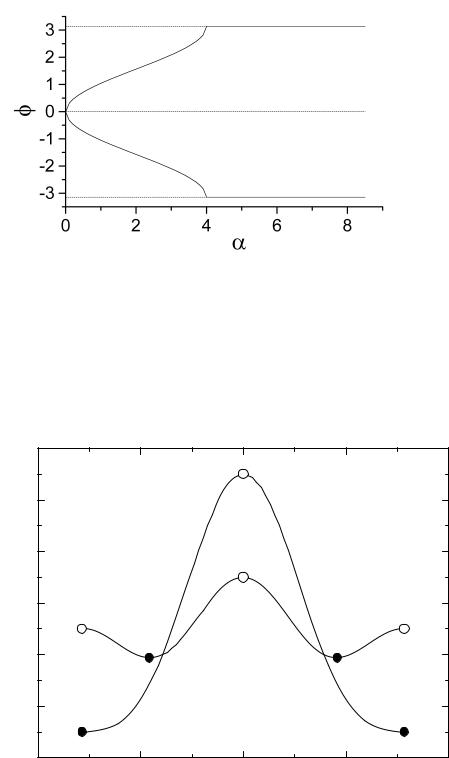
Строим диаграмму устойчивости (рис. 2) положений равновесия (бифуркационную диаграмму). Сплошные линии соответствуют устойчивым положениям равновесия, пунктирные – неустойчивым.

На диаграмме устойчивости существует две точки, в которых происходит бифуркация (удвоение количества) решений: (ϕ=0, α=0) и (ϕ=±π, α=4). Отметим, что два значения угла ϕ=±π соответствуют одной и той же физической ситуации, когда груз 1 занимает крайнее нижнее положение.

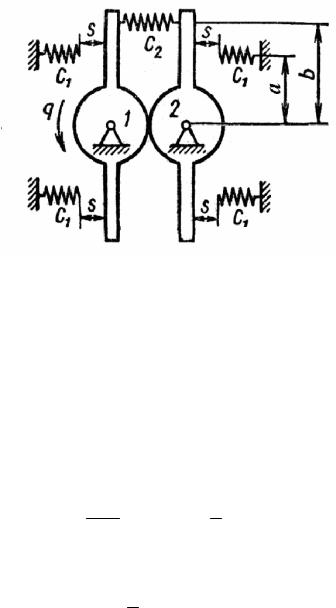
Строим зависимость потенциальной энергии от угла ϕ при значениях параметра α, соответствующих различным количествам положений равновесия: α=0; 1; 2; 3; 4; 5 и т.д. На рис. 3 в качестве примеров построены зависи-

мости потенциальной энергии (в единицах 2Gl2 ) от угла поворота стержня 4 при двух значениях параметра α=2.5 (кривая 1) и 4.5 (кривая 2). Светлые

12

ЗАДАЧА 2

Интегрирование уравнений движения системы с кусочно-линейной характеристикой методом припасовывания (сшивки решений)

Условие задачи.

Система состоит из нескольких тел и пружин, жесткости ci которых обозначены на рисунках (см. с. 18 – 20). Заданы массы и/или моменты инерции тел системы. Необходимо сформулировать дифференциальное уравнение движения системы, проинтегрировать его при заданных начальных условиях, определить период колебаний и построить фазовую траекторию.

Рисунки на стр. 37–39.

Методические указания и пример решения задачи

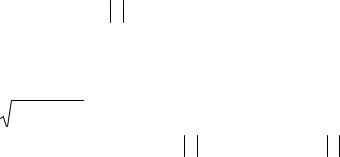
Дано: m=20кг, i=0,1м, c1=2,5н/см, a=0,2м, b=0,25м, c2=1,0н/см, s=0.02м, q0=0.2 рад, q0 = 0 . При вертикальных стержнях пружина 2 не напряжена, i – радиус инерции тел 1 и 2 относительно их осей вращения (см. рис. 4).

Необходимо: построить фазовую траекторию системы и определить период коле-

Рис. 4. баний.

Решение.

2.1. Составление дифференциального уравнения движения

Воспользуемся уравнением Лагранжа

В качестве обобщенной координаты выберем угол поворота тела 1. Кинетическая энергия системы, состоящей из двух вращающихся тел

Κ = 2 Jq22 = mi2 q 2 = 12 J прq 2 ,

где момент инерции тела J=mi2; i – радиус инерции; Jпр=2mi2 – приведенный момент инерции системы. Потенциальная энергия системы

Π = c1λ21 + 12 c2 λ22 .

Здесь учтено, что одновременно работают две пружины жесткости с1. Деформации пружин при условии малых колебаний (tgq q) определяются сле-

13

дующими соотношениями:

λ2 = 2bq.

Знаки деформаций выбраны так, чтобы растянутым пружинам соответствовали положительные деформации. Пружины жесткости с1 работают только на сжатие, пружина жесткости с2 бывает сжатой или растянутой в зависимости от знака обобщенной координаты q.

В результате потенциальная энергия системы

Правая часть уравнения (2) представляет собой обобщенную силу Q, которая является кусочно-линейной функцией обобщенной координаты. Ее график (характеристика) представлен на рис. 5. Здесь римскими цифрами отмечены три участка значений q>s/a, q < s / a и q<-s/a.

Окончательно дифференциальное уравнение движения представим как

тервалу изменения обобщенной координаты q < s / a, а i=2 − q > S / a.