лесная биометрия

Вычисление основных статистик с помощью ПЭВМ

Вычисление основных статистик с помощью пакета Statistica 6.0 можно выполнить следующим образом.

1.Запустить программу Statistica, нажав кнопку «Пуск» и вы-

брав следующие опции: «Программы», «Statistica 6.0», «Statistica».

2.Открыть созданный ранее файл с исходными данными, активизировав опцию «Открыть …» из меню «Файл».

3.Выбрав опцию «Основная статистика/таблицы» из меню «Статистика», открыть диалоговое окно, содержащее локальное меню. Из данного меню выбрать опцию «Descriptive statistics», активизировав ее кнопкой «OK».

4.В открывшемся диалоговом окне «Descriptive Statistics» нажмем кнопку «Variables». После этого на экране появится еще одно

30

диалоговое окно, содержащее список переменных. Выбрать какуюнибудь переменную, или сразу все, нажав кнопку «Select All». Завершить выбор переменных нажатием кнопки «OK».

5.Далее в диалоговом окне «Descriptive Statistics» надо выбрать вкладку «advanced». Затем с помощью мыши установить флажки против тех статистик, которые следует вычислить, или выбрать все параметры, нажав кнопку «Advanced».

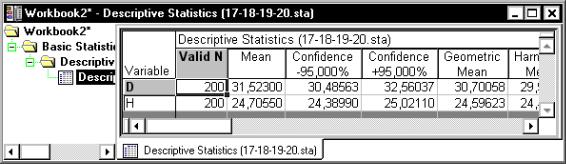
6.Для выполнения вычислений следует нажать кнопку «Summary». На экране появится таблица, содержащая вычисленные основные статистики для выбранных переменных (рис. 7). Полученные результаты сведены в табл. 11, где, кроме статистик, приведены английские названия вычисленных показателей, используемые в программе Statistica, и их русские эквиваленты.

Рис. 7. Результаты вычисления основных статистик с помощью программы Statistica

Построение доверительных интервалов

Доверительным интервалом для параметра θ называется интервал ]Θ€ −ε;Θ€ + ε[, который с заданной доверительной вероятностью

p = 1–α накрывает этот параметр. Построим доверительные интервалы для параметров нормального распределения. Это распределение имеет два параметра: m – математическое ожидание и σ – среднеквадратическое отклонение. В том случае, если точечные оценки параметров m и σ получены на основании выборки, доверительный интервал для математического ожидания строится с использованием квантилей распределения Стьюдента для уровня значимости α/2 и числа степеней свободы n–1 (прил., табл. 3) следующим образом:

31

Таблица 11. Основные статистики для диаметров и высот деревьев в

древостое

распределения χ2, соответствующие числу степеней свободы γ = n–1 и уровням значимости α/2 и 1–α/2. Коэффициенты γ1 и γ2 приведены в прил. (табл. 4).

Рассмотрим пример вычисления доверительных интервалов для параметров нормального распределения по материалам вариационных рядов диаметров и высот. Используя средние арифметические двухсот измеренных диаметров и высот, вычисленные ранее (3) и (4), а также среднеквадратические отклонения (13) и (14) и исходя из предположения, что диаметры деревьев подчиняются закону нормального распределения, найдем доверительные интервалы, накрывающие параметры m и σ с доверительной вероятностью 0,95. В таблице квантилей

распределения Стьюдента 3 в приложении находим t0,025;199 = 1,972. Тогда доверительный интервал для среднего арифметического значе-

Для того чтобы вычислить границы доверительных интервалов для среднеквадратического отклонения, найдем по табл. 4 прил. коэффициенты γ1 = 0,912 и γ2 = 1,11 для уровня значимости α = 0,05. Используя точечные оценки среднеквадратических отклонений для данных по диаметрам (13) и высотам (14) и с учетом выражения (19), получаем доверительные интервал для среднего квадратического отклонения:

]7,455 0,912; 7,455 1,11[, или ]6,799; 8,275[ – диаметры; ]2,278 0,912; 2,278 1,11[, или ]2,078; 2,529[ – высоты.

33

АНАЛИЗ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН

Любая случайная величина подчинена какому-либо, как правило, неизвестному закону распределения. Одной из задач биометрии и является определение закона распределения анализируемой случайной величины. Обычно решение этой задачи начинается с проверки гипотезы о нормальном распределении данных.

Нормальное распределение

Нормальное распределение имеет важное значение в биометрии. На практике очень часто исследуемые случайные величины следуют этому закону. Для того чтобы узнать, подчиняется случайная величина закону нормального распределения или нет, надо вычислить теоретические частоты вариационного ряда исходя из предположения о нормальном распределении анализируемого параметра и сравнить их с эмпирическими частотами.

Закон распределения случайной величины может быть описан с помощью функции, определяемой соотношением

FX (x) = P(X < x)

и называемой функцией распределения величины X.

Разность F (b) − F (a) представляет собой вероятность того, что случайная величина X примет значение, принадлежащее интервалу a ≤ X < b, т. е. если a и b являются нижней и верхней границами интервала вариационного ряда, то вероятность попадания изучаемой случайной величины в данный интервал можно вычислить так:

Зная эту величину, нетрудно вычислить теоретическое число наблюдений для данного интервала fa,b = n Pa,b .

Функция нормального распределения F(x) имеет вид

Сучетом функции нормального распределения (21) выражение

(20)можно переписать следующим образом:

34

Интегралы, входящие в это выражение, нельзя выразить через элементарные функции, но их можно вычислить через специальную функцию:

которая является интегральной функцией нормального распределения с параметрами m = 0 и σ = 1. Для этого следует перейти к нормиро-

ванной случайной величине:

T = X σ−m .

С помощью (24) и данных табл. 2 прил. мы можем вычислить теоретические частоты вариационного ряда, предполагая, что иссле-

35

дуемая случайная величина распределена по нормальному закону. Выполним эту работу для вариационных рядов по диаметру и

высоте. Для выполнения вычислений составим вспомогательную таблицу (табл. 12). С учетом того, что оценкой параметров нормального распределения методом моментов являются среднеквадратическое отклонение и среднее арифметическое, вычислим нормированные нижнюю и верхнюю границы интервалов следующим образом:

Таблица 12. Вычисление теоретических частот для функции нормаль-

ного распределения (диаметры)

В отличие от анализируемого вариационного ряда, нормальное распределение определено на интервале от –∞ до +∞. Для того чтобы области определения эмпирического и нормального распределения сделать одинаковыми, добавим дополнительные интервалы перед первым интервалом с границами от –∞ до нижней границы первого интервала и после последнего интервала с границами от верхней границы последнего интервала до +∞. Эмпирические частоты этих дополнительных интервалов будут равны нулю, так как в исходных дан-

36

ных нет ни одного наблюдения, которое было бы меньше нижней границы первого интервала или больше верхней границы последнего интервала. Значения функции нормированного нормального распределения для нижней Ф(tiн) и верхней Ф(tiв) границ интервалов можно найти с помощью табл. 2, используя в качестве аргументов значения tiн и tiв соответственно. В этой таблице значения функции распределения даны только для положительных аргументов. Если надо найти функцию распределения для отрицательного аргумента, следует воспользоваться соотношением Ф(–x) = 1–Ф(x), которое справедливо, так как нормальное распределение является симметричным.

Вероятности для интервалов вариационного ряда легко вычислить как разность значений функции распределения для верхней и нижней границ:

Pi = Φ(tiв) −Φ(tiн) .

Теперь можно найти теоретические частоты ряда: fi = n Pi .

Аналогичным образом можно вычислить теоретические частоты для вариационного ряда высот (табл. 13).

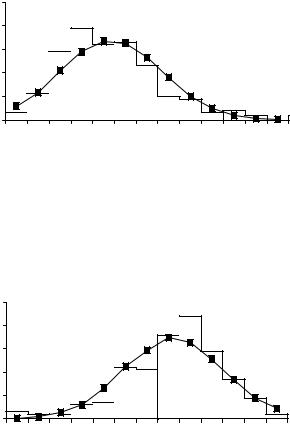
Последние колонки табл. 12 и 13, представляющие собой разность между эмпирическими и теоретическими частотами, дают нам информацию о близости теоретического (в данном случае нормального) и эмпирического распределений. Однако по данным отклонениям достаточно трудно принять решение о согласованности эмпирического и теоретического распределений. Более наглядную картину можно увидеть, изобразив эти распределения графически (рис. 8 и 9). Однако такие сравнения распределений будут субъективными. Для того чтобы дать объективную оценку согласованности эмпирических и теоретических распределений, необходимо воспользоваться специальными методиками проверки статистических гипотез.

Статистическая проверка непараметрических гипотез

Для того чтобы выяснить, подчиняются ли экспериментальные данные какому-либо закону распределения, надо сформулировать статистическую гипотезу в отношении распределения анализируемой случайной величины и затем проверить ее. Для проверки гипотез, выдвигаемых в отношении вида распределения, используются специальные статистики, называемые непараметрическими критериями или

37

критериями согласия. Рассмотрим процесс проверки непараметрической гипотезы с помощью одного из критериев согласия – критерия Пирсона. На первом этапе следует выдвинуть нулевую гипотезу, состоящую в том, что анализируемый признак подчиняется какому-либо закону распределения. Далее, исходя из предположения о том, что нулевая гипотеза справедлива, следует вычислить статистику χ2:

Таблица 13. Вычисление теоретических частот для функции нормаль-

ного распределения (высоты)

Полученное значение сравнивается с квантилем распределения Пирсона χ2, приведенного в табл. 5 приложения. В качестве параметров распределения используется уровень значимости (обычно используется α = 0,05) и число степеней свободы:

где k – общее число степеней свободы, равное числу слагаемых в сумме из формулы (25); ρ – число параметров теоретической функции распределения, которые оценивались по анализируемым данным.

38