
- •1. Элементы комбинаторики: размещения, перестановки, сочетания. Привести примеры.
- •7. Теорема сложения вероятностей. Привести пример.
- •12. Локальная формула Муавра-Лапласа. Привести пример.
- •18. Дисперсия дискретной случайной величины (определение, формула для вычисления). Основные свойства дисперсии.
- •25. Показательный закон распределения. Привести пример.
- •27. Система двух дискретных св. Функция распределения и её свойства.
- •28. Безусловные законы распределения составляющих системы св
- •29.Корреляционный момент и коэффициент корреляции. Свойства коэффициента корреляции.
- •30. Основные задачи математической статистики.
- •31. Генеральная и выборочная совокупности (гс и вс). Свойство репрезентативности выборки.
- •32. Статистический ряд, интервальный статистический ряд, статистическое распределение.
- •33. Полигон и гистограмма статистического ряда.
- •34. Эмпирическая функция распределения и её основные свойства.
- •35. Статистическая оценка неизвестных параметров распределения. Виды оценок.
- •36. Классификация точечных оценок (состоятельные, несмещённые, эффективные).
- •37.Выборочное среднее и свойство устойчивости среднего.
- •38. Выборочная оценка дисперсии. Несмещённая оценка дисперсии.
- •43. Эмпирическая линейная регрессия.
- •44. Примеры задач линейного программирования.
- •45. Общая и каноническая злп. Переход от общей задачи к канонической.
- •46. План злп, область допустимых планов, базисный (опорный) план, невырожденный план, базисные переменные.
- •47. Графический метод решения злп.
- •48. Симплекс-метод решения злп: идея метода и построение первоначального базисного плана. Симплексная таблица.
- •48-1. Симплекс-метод решения злп: проверка плана на оптимальность.
- •49. Симплекс-метод решения злп: переход к новому плану.
- •50. Метод искусственного базиса (м-задача)
- •51. Транспортная задача. Математическая постановка задачи.
- •52. Условие разрешимости тз. Закрытая модель тз
- •53. Построение первоначального опорного плана тз
- •54. Условия оптимальности опорного плана. Метод потенциалов.
- •55. Циклы в транспортной задаче. Построение нового опорного плана.
- •56. Прямая и двойственная задачи.
- •57. Связь между решениями прямой и двойственной задачи (основные теоремы)
- •58. Геометрическая интерпретация двойственной задачи.
- •59. Нахождение решения двойственной задачи.
- •60. Экономическая интерпретация двойственных задач.
25. Показательный закон распределения. Привести пример.
Показательное (экспоненециальное) распределение. Непрерывная случайная величина, принимающая неотрицательные значения, имеет показательное распределение с параметром>0, если плотность распределения вероятностей случайной величины равна
р(x)=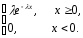
Функция распределения показательного распределения имеет вид
F(x)=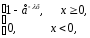
а
математическое ожидание и дисперсия
равны М=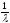 ,
D=
,
D=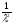 .
.
26.
Нормальный закон распределения и его
особенности. Привести пример.
Нормальное
распределение(распределение Гаусса).
Непрерывная случайная величина
называется распределенной по нормальному
закону с параметрами и
и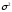 ,
если ее плотность распределения равна
,
если ее плотность распределения равна
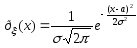 .
.
Через
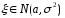 обозначается множество всех случайных
величин, распределенных по нормальному
закону с параметрами параметрами
обозначается множество всех случайных
величин, распределенных по нормальному
закону с параметрами параметрами и
и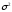 .
.
Функция распределения нормально распределенной случайной величины равна
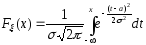 .
.
Параметры
нормального распределения суть
математическое ожидание
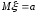 и дисперсия
и дисперсия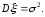
В
частном случае, когда
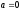 и
и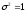 нормальное распределение называетсястандартным, и класс таких распределений
обозначается
нормальное распределение называетсястандартным, и класс таких распределений
обозначается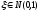 .
.
В этом случае плотность стандартного распределения равна
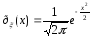 ,
а функция распределения
,
а функция распределения
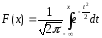
Поэтому
вероятность попадания нормально
распределенной случайной величины
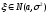 на интервал
на интервал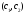 можно вычислять по формуле
можно вычислять по формуле
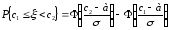 .
.
Неотрицательная
случайная величина называется логарифмически нормально
распределенной, если ее логарифм=ln
подчинен нормальному закону.
Математическое ожидание и дисперсия
логарифмически нормально распределенной
случайной величины равныМ=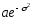 и
и
D=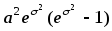 .
.
27. Система двух дискретных св. Функция распределения и её свойства.
Будем обозначать через (X,Y) двумерную случайную величину. Каждую из величинXиYназывают составляющей (компонентой); обе величиныXиY, рассматриваемые одновременно, образуютсистему двух случайных величин.
Функцией распределениядвумерной случайной величины (X,Y) называют функциюF(x,y), определяющую для каждой пары чиселx,yвероятность того, чтоXпримет значение, меньшееx, и при этомYпримет значение, меньшееy:F(x,y) =P(X<x,Y<y).
Свойство
1.Значения функции распределения
удовлетворяют двойному неравенству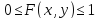 .
.
Свойство 2.F(x,y) есть неубывающая функция по каждому аргументу, т.е.
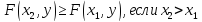 ;
;
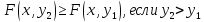
Свойство 3.Имеют место предельные соотношения:
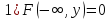 ;
2)
;
2)
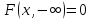 ;
3)
;
3)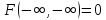 ;
4)
;
4)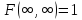
Свойство
4.а) При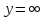 функция распределения системы становится
функцией распределения составляющей
Х:
функция распределения системы становится
функцией распределения составляющей
Х: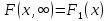 .
.
б) При
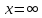 функция распределения системы становится
функцией распределения составляющей
Х:
функция распределения системы становится
функцией распределения составляющей
Х: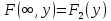 .
.
28. Безусловные законы распределения составляющих системы св
Условные. 1) Для дискретной двумерной С.В.
Пусть составляющие X и Y дискретны и имеют соответственно следующие возможные значения: x1,x2,…,xn; y1,y2,…,ym.
Условным распределением составляющей Х при Y=yj (j сохраняет одно и то же значение при всех возможных значениях Х) называют совокупность условных вероятностей p(x1|yj), p(x2|yj),…,p(xn|yj).
Аналогично определяется условное распределение Y.
Условные вероятности составляющих Х и Y вычисляют соответственно по формулам: p(xj|yi)=p(xi,yj)/p(yj), p(yj|xi)=p(xi,yj)/p(xi).
