
- •1. Элементы комбинаторики: размещения, перестановки, сочетания. Привести примеры.
- •7. Теорема сложения вероятностей. Привести пример.
- •12. Локальная формула Муавра-Лапласа. Привести пример.
- •18. Дисперсия дискретной случайной величины (определение, формула для вычисления). Основные свойства дисперсии.
- •25. Показательный закон распределения. Привести пример.
- •27. Система двух дискретных св. Функция распределения и её свойства.
- •28. Безусловные законы распределения составляющих системы св
- •29.Корреляционный момент и коэффициент корреляции. Свойства коэффициента корреляции.
- •30. Основные задачи математической статистики.
- •31. Генеральная и выборочная совокупности (гс и вс). Свойство репрезентативности выборки.
- •32. Статистический ряд, интервальный статистический ряд, статистическое распределение.
- •33. Полигон и гистограмма статистического ряда.
- •34. Эмпирическая функция распределения и её основные свойства.
- •35. Статистическая оценка неизвестных параметров распределения. Виды оценок.
- •36. Классификация точечных оценок (состоятельные, несмещённые, эффективные).
- •37.Выборочное среднее и свойство устойчивости среднего.
- •38. Выборочная оценка дисперсии. Несмещённая оценка дисперсии.
- •43. Эмпирическая линейная регрессия.
- •44. Примеры задач линейного программирования.
- •45. Общая и каноническая злп. Переход от общей задачи к канонической.
- •46. План злп, область допустимых планов, базисный (опорный) план, невырожденный план, базисные переменные.
- •47. Графический метод решения злп.
- •48. Симплекс-метод решения злп: идея метода и построение первоначального базисного плана. Симплексная таблица.
- •48-1. Симплекс-метод решения злп: проверка плана на оптимальность.
- •49. Симплекс-метод решения злп: переход к новому плану.
- •50. Метод искусственного базиса (м-задача)
- •51. Транспортная задача. Математическая постановка задачи.
- •52. Условие разрешимости тз. Закрытая модель тз
- •53. Построение первоначального опорного плана тз
- •54. Условия оптимальности опорного плана. Метод потенциалов.
- •55. Циклы в транспортной задаче. Построение нового опорного плана.
- •56. Прямая и двойственная задачи.
- •57. Связь между решениями прямой и двойственной задачи (основные теоремы)
- •58. Геометрическая интерпретация двойственной задачи.
- •59. Нахождение решения двойственной задачи.
- •60. Экономическая интерпретация двойственных задач.
18. Дисперсия дискретной случайной величины (определение, формула для вычисления). Основные свойства дисперсии.
Дисперсией![]() ДСВ
ДСВ![]() называется математическое ожидание
квадрата отклонения СВ от ее математического
ожидания
называется математическое ожидание
квадрата отклонения СВ от ее математического
ожидания
![]()
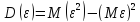
![]()
Дисперсия служит для характеристики рассеяния СВ относительно ее математического ожидания
Свойства дисперсии:
а)
![]() ,
где
,
где![]() ;
;
б)
![]() ;
;
в)![]() ,
,
где
![]() – ковариация двух случайных величин
– ковариация двух случайных величин![]() и
и![]() ;
;
г) если
![]() и
и![]() некоррелированы, то
некоррелированы, то![]() ,
тогда
,
тогда![]() .
.
19.
Биномиальное распределение и его
числовые характеристики. Привести
пример.
Биномиальный
закон распределения.Случайная
величина![]() ,
распределенная по биномиальному закону,
принимает значения:
,
распределенная по биномиальному закону,
принимает значения:
0, 1, 2,
…, nс вероятностями,
определяемыми по формулам Бернулли:![]()
|
|
0 |
1 |
2 |
,,, |
|
,,, |
|
|
|
|
|
|
|
|
|
|
Числовые
хар-ки: Математическое ожидание:
![]() .
Дисперсия:
.
Дисперсия:![]() .
.
Пример.В рекламных целях торговая фирма вкладывает в каждую пятую единицу товара денежный приз размером 100 тенге. Найти закон распределения числа сотен тенге, полученных при четырёх сделанных покупках.
20.
Распределение Пуассона и его числовые
характеристики. Привести пример.Закон
распределения Пуассона. Случайная
величина![]() ,
распределенная по закону Пуассона,
принимает бесконечное счетное число
значений: 0, 1, 2, …,m, …, с
соответствующими вероятностями,
определяемыми по формуле Пуассона
,
распределенная по закону Пуассона,
принимает бесконечное счетное число
значений: 0, 1, 2, …,m, …, с
соответствующими вероятностями,
определяемыми по формуле Пуассона
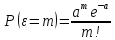 При
При
![]() и
и![]() биномиальный закон распределения
приближается к закону распределения
Пуассона, гдеa=np
биномиальный закон распределения
приближается к закону распределения
Пуассона, гдеa=np
Математическое ожидание M(ξ) = ДисперсияD(ξ) =a.
Пример: число родившихся за определённый период близнецов, число опечаток в большом тексте.
21. Непрерывные случайные величины. Способы задания закона распределения (функция распределения, плотность вероятности). Привести пример. Функция распределения представляет собой универсальный способ задания СВ в том смысле, что она существует только для дискретной СВ, а плотность распределения – только для непрерывной.
Для
непрерывной СВ функция распределения
F(x)=P(ξ<x)
непрерывна в любой точке числовой
прямой. Более того, P(ξ=x0)=0,
т.е. вероятность
того, что непрерывная СВ примет заранее
указанное значение, равна нулю.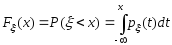
F(x) можно представить в виде интеграла
Функция
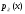 называется функциейплотности
распределения вероятностей.
называется функциейплотности
распределения вероятностей.
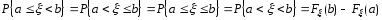
22.
Плотность вероятности Основные
свойства.
Функция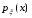 называется функциейплотности
распределения вероятностей.
называется функциейплотности
распределения вероятностей.
Из
определения вытекают свойства функции
плотности распределения
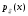 :
:
1.Плотность
распределения неотрицательна:
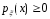 .
.
2.
Интеграл по всей числовой прямой от
плотности распределения вероятностей
равен единице:
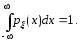
3. В
точках непрерывности плотность
распределения равна производной функции
распределения:
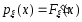 .
.
4.
Плотность распределения определяет
закон распределения случайной величины,
т.к. определяет вероятность попадания
случайной величины на интервал
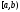 :
:
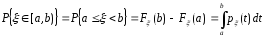 .
.
5.
Вероятность того, что непрерывная
случайная величина примет конкретное
значение
 равна нулю:
равна нулю: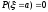 .
Поэтому справедливы следующие равенства:
.
Поэтому справедливы следующие равенства:
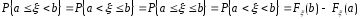 23.
Числовые характеристики непрерывной
СВ.
Математическое
ожидание
для непрерывно распределенных случайных
величин определяется по формуле
23.
Числовые характеристики непрерывной
СВ.
Математическое
ожидание
для непрерывно распределенных случайных
величин определяется по формуле
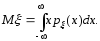 При этом интеграл, стоящий справа, должен
абсолютно сходиться. Пусть
имеет плотность р(х) и (х)
- некоторая функция. Математическое
ожидание величины ()
можно вычислить по формуле
При этом интеграл, стоящий справа, должен
абсолютно сходиться. Пусть
имеет плотность р(х) и (х)
- некоторая функция. Математическое
ожидание величины ()
можно вычислить по формуле
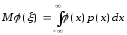 ,
если интеграл, стоящий справа, абсолютно
сходится.
,
если интеграл, стоящий справа, абсолютно
сходится.
Дисперсия
может быть вычислена по формуле
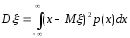 ,
а также, как и в дискр-ом случае, по
ф-ле
,
а также, как и в дискр-ом случае, по
ф-ле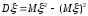 ,
где
,
где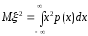 24.
Равномерный закон распределения и его
числовые характеристики. Пример.
Равномерное
распределение. Непрерывная
случайная величинаимеет равномерное распределение на
отрезке [a,b], если плотность распределения
р(x) сохраняет
постоянное значение на этом промежутке:
24.
Равномерный закон распределения и его
числовые характеристики. Пример.
Равномерное
распределение. Непрерывная
случайная величинаимеет равномерное распределение на
отрезке [a,b], если плотность распределения
р(x) сохраняет
постоянное значение на этом промежутке:
Функция
распределения F(x)
равномерно распределенной случайной
величины равна F(x)=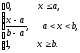
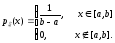
Математическое
ожидание и дисперсия 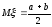 ;
;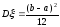 .
.
