7. Теорема сложения вероятностей. Привести пример.

Теорема сложения вероятностей

Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:

Р (А + В) = Р (А) + Р (В). В случае, когда события А и В совместны, вер-ть их суммы выражается формулой Р (А +В) = Р (А) + Р (В) – Р (АВ), где АВ – произведение событий А и В.

Пример 2. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую — 0,35. Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.

Р е ш е н и е. События А — "стрелок попал в первую область" и В — "стрелок попал во вторую область" — несовместны (попадание в одну область исключает попадание в другую), поэтому теорема сложения применима.

Искомая вероятность Р (А + В) = Р (А) + Р (В) = 0,45 + 0,35 = 0,80.

8. Зависимые и независимые события. Условная вероятность. Теорема умножения вероятностей. Привести пример. Два события называются зависимыми, если вероятность одного из них зависит от наступления или не наступления другого. в случае зависимых событий вводится понятие условной вероятности события.

Условной вероятностью Р(А/В) события А называется вероятность события А, вычисленная при условии, что событие В произошло. Аналогично через Р(В/А) обозначается условная вероятность события В при условии, что событие А наступило.

Теорема  умножения вероятностей

Вероятность произведения двух событий равна вер-ти одного из них, умноженной на условную вероятность другого при наличии первого: Р (АВ) = Р(А) · Р(В/А), или Р (АВ) = Р(В) · Р(А/В).

Пример теоремы умножения для независимых событий. Найти вероятность совместного появления герба при одном бросании двух монет.

Пример независимого события. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие A) равна 0,8, а вторым (событие В) — 0,7.

Пример условной вероятности. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).

9. Формула полной вероятности. Привести пример. Если об обстановке опыта можно сделатьnисключающих друг друга предположений (гипотез)

Н₁, Н₂, ..., Н_nи если событиеАможет появиться только при одной из этих гипотез, то вероятность событияАвычисляется поформуле полной вероятности:

Р(А) = Р(Н₁) Р(А/Н₁) + Р(Н₂) Р(А/Н₂) +...+  Р(Н_n) Р(А/Н_n).

Пример.Из 40 деталей 10 изготовлены в первом цехе, 25 - во втором, а остальные - в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех - с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества?

10. Схема Бернулли. Формула Бернулли. Привести пример. Последовательность n независимых в совокупности испытаний называется схемой Бернулли, если при каждом испытании возможны только два исхода: появление события А (успех) и его непоявление (неуспех), причём вероятность появления события А в каждом из n независимых испытаний постоянна и равна p.

В схеме Бернулли вероятность того, что в n испытаниях событие А наступит ровно m раз, вычисляется по формуле Бернулли:

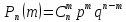, где q=1-p; ; n!=n·(n-1)·…·2·1, 0!=1.

Пример. Вероятность попадания в мишень при каждом выстреле равна 0,4. По мишени производится шесть независимых выстрелов. Найдите вероятность хотя бы одного попадания в мишень.

11. Формула Пуассона. Привести пример. Если в схеме Бернулли вероятность p появления события А в каждом из n независимых испытаний очень мала, а число испытаний n достаточно велико, то вероятность вычисляется приближенно по формуле Пуассона: , a=n·p.

Эту формулу обычно применяют в тех случаях, когда а ≤ 10.

Пример. Среди семян ржи 0,04% сорняков. Какова вероятность, что при случайном отборе 5000 семян обнаружить ровно 5 семян сорняков.