ЛАБОРАТОРНАЯ РАБОТА № 4

Элементы теории корреляционного и регрессионного анализа

1. Теоретические сведения.

Корреляционный анализ исследует взаимосвязь случайных величин (СВ) на основе экспериментальных данных. Предположим, что результаты эксперимента описываются двумя СВ и . Они могут быть 1) независимы; 2) связаны функциональной зависимостью; 3) связаны статистической зависимостью.

СВ связаны функциональной зависимостью, если одна из них является функцией другой.

Статистической называется зависимость, при которой изменение одной величины влечет изменение распределения другой. Статистическая зависимость возникает из-за того, что на результат эксперимента влияют какие-то неучтенные случайные факторы.

Для определения статистической зависимости данные наблюдений СВ и Y - двумерной СВ (X,Y), записывают в виде корреляционной таблицы 1

Таблица 1

Y X			…
			…
			…
			…
			…

где,

; ; .

Здесь означает, что пара значений () наблюдалось раз, и соответствующие частоты наблюдаемых значений и , ; .

В случае, когда число наблюдаемых значений СВ и Y велико или СВ являются непрерывными ( т.е. могут принимать любое значение из соответствующих интервалов), аналогично интервальному статистическому ряду (лаб. раб. №3) составляется интервальная корреляционная таблица.

Условным средним называют среднее арифметическое значений СВ Y, соответствующих значению . Например,

.

Корреляционной зависимостью Y от называют зависимость условной средней от x:

(1)

Уравнение (1) называют эмпирическим уравнением регрессии Y на X; функцию называют эмпирической регрессией Y на X, а ее график - линией регрессии Y на X .

Аналогично определяются условная средняя и корреляционная зависимость от Y:

(2)

Предварительное представление о характере зависимости между и можно получить, если элементы выборки , , отметить в виде точек на плоскости в выбранной системе координат. Эта точечная диаграмма называется корреляционным полем.

Распределение системы СВ характеризуется числовыми параметрами: математическими ожиданиями компонент , ; дисперсиями , ; корреляционным моментом (ковариацией) ; коэффициентом корреляции , .

Здесь и дальше, будем считать, что двумерная СВ распределена нормально, тогда уравнения линейной регрессии на и на имеют вид [7]:

и

По корреляционной таблице 1, найдем оценки параметров линейной регрессии, ( см. лаб. раб. №3):

; ; (3)

; (4)

; (5)

; (6)

- выборочный коэффициент корреляции . (7)

Выборочный коэффициент корреляции характеризует тесноту линейной связи между и . Если , то элементы выборки , лежат на прямой линии, а и считаются практически линейно зависимы. Чем ближе к 1, тем связь сильнее; чем ближе к 0, тем связь слабее. Если и независимы, то .

Эмпирическая функция линейной регрессии на и на соответственно задаётся уравнениями

; .

Замечание 1. Если построить на одном корреляционном поле две линии регрессии на и на , то они пересекутся в точке O, и угол между этими прямыми тем меньше, чем ближе коэффициент корреляции к .

Замечание 2. В случае, когда данные наблюдений СВ и Y записаны в виде интервальной корреляционной таблицы в формулах (3) – (7) вместо и обычно берут середины, соответствующих интервалов.

Замечание 3. Если наблюдаемые значения СВ большие числа, то чтобы упростить вычисления, вводятся условные переменные (варианты) для корреляционной таблицы 1 и ; для интервальной корреляционной таблицы.

За условные нули и , обычно, принимают наблюдаемые значения , или средины интервалов, имеющие наибольшую частоту . Формулы, связующие числовые характеристики СВ и СВ (U,V) имеют вид:

; ; ; ;

.

Для проверки при заданном уровне значимости , нулевой гипотезы : о некоррелированности составляющих и , нормально распределенной двумерной СВ , при конкурирующей гипотезе , вычисляется наблюдаемое значение критерия

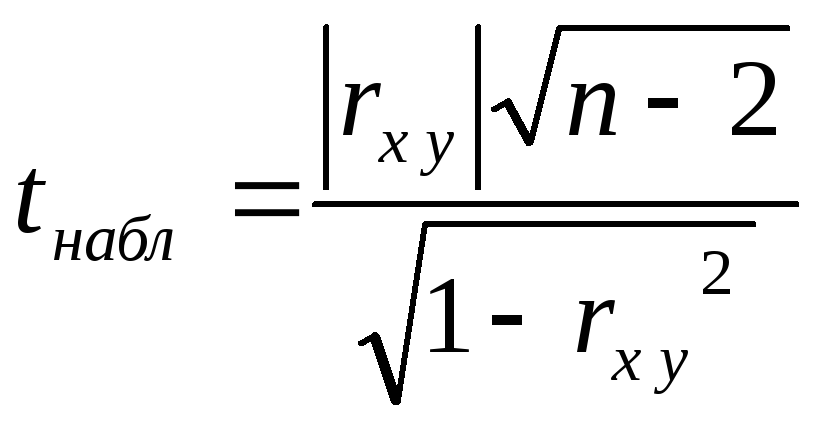
и по таблице критических точек распределения Стьюдента по заданному уровню значимости и числу степеней свободы , находится . Затем сравнивается наблюдаемое значение критерия с табличным.

Если , то гипотеза о некоррелированности составляющих и отвергается. Если же , то нет основания отвергать нулевую гипотезу о некоррелированности случайных величин и [6-8].