дифуравнения / дифуравнения-1 / тема2

Тема: Однорідні рівняння першого порядку.

Теоретичні відомості.

Означення 1. Функція називається однорідною функцією го виміру, якщо для будь – якого виконується рівність .

Приклад 1. Функція є однорідною функцією третього виміру, бо .

Функція є однорідною функцією нульового виміру, тому що .

Означення 2. Диференціальне рівняння першого порядку

, (1.4)

називається однорідним, якщо функція є однорідною функцією нульового виміру відносно і .

Отже, згідно з означенням, для будь – якого . Оберемо і отримаємо , тобто і функція залежить лише від відношення аргументів . Тому рівняння (1.4) може бути записане у вигляді

. (1.5)

Введемо допоміжну функцію , і оскільки , то . Отримаємо рівняння з подільними змінними

. (1.6)

Розв’яжемо його: Далі знаходимо інтеграл в лівій частині рівняння, замінюємо в ньому і отримаємо загальний інтеграл рівняння (1.4).

Для того, щоб розв’язати однорідне рівняння, необхідно:

1. Переконатися в тому, що рівняння однорідне, і записати його у вигляді (1.4).

2. Покласти , .

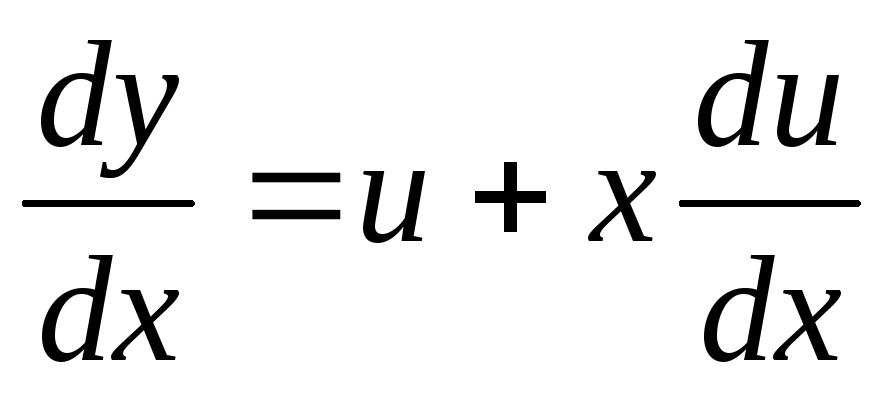3. Скоротити дріб на (повністю), перенести в ліву частину і спростити її.

4. Розділити змінні (справа завжди 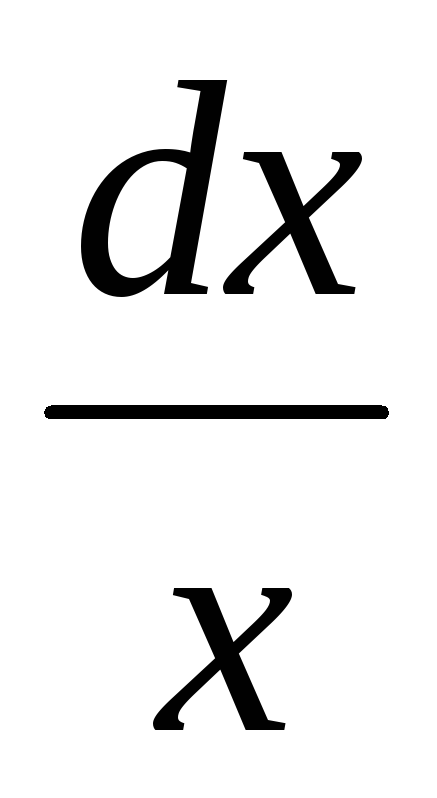) і про інтегрувати.

5. Замінити 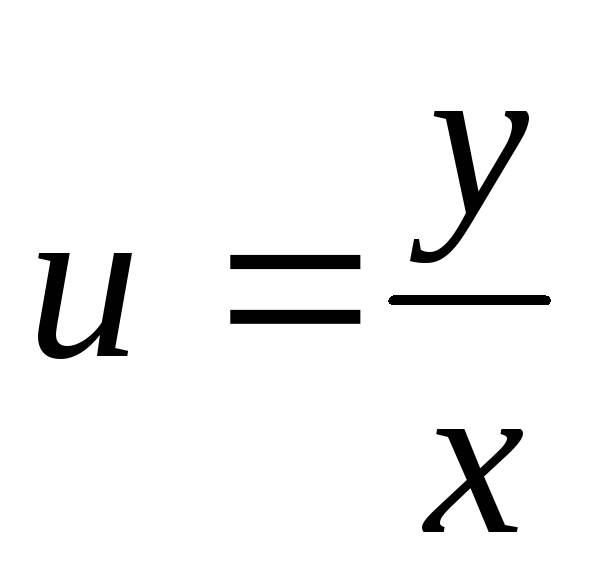і спростити.

Зауважимо, що рівняння є однорідним, якщо і є однорідними функціями однакового виміру.

Практичні завдання.

Завдання 1. Доведіть, що функція є однорідною функцією першого виміру, а функція є однорідною функцією другого виміру.

Завдання 2. Знайти загальний інтеграл (рішення) диференціального рівняння:

2.1. .

2.2. .

2.3. .

2.4. .

2.5. .

2.6. .

2.7. .

2.8. .

Завдання 3. Розв’язати задачу Коші:

2.9. , якщо .

2.10. , якщо .

2.11. , якщо .

2.12. , якщо .

2.13. , якщо .

Домашнє завдання: теоретичні відомості

Знайти загальний інтеграл рівняння .

Знайти частинний інтеграл рівняння , якщо .