Дисциплина «Математические модели информационных процессов и управления»

1. Определение графа, его специальные разновидности и классы.

Графом G называется система , где 1) V={v} – множество вершин графа; 2) E={e} – множество ребер графа, причем ; 3) – функция инцидентности, ставящая в соответствие каждому ребру е вершину или пару вершин (V₁,V₂).

Эти вершины называются концевыми вершинами. Ребро е находится в отношении инцидентности со своими вершинами (V₁,V₂) и пишут: е=(V₁,V₂).

Множество образует множество элементов графа. По количеству элементов графы могут быть конечные и бесконечные. Для обозначения вершин используются буквы V₁,V₂,… . Для обозначения ребер используются буквы е₁,е₂,…

Если ребра графа определяются упорядоченными парами, то граф называется ориентированным. В противном случае неориентированным.

Упорядоченная пара (V_i,V_j) есть такая, что если V_i≠V_j, то (V_i≠V_j)= (V_j≠V_i).

Если задана функция или , то множество М называется множеством пометок, а граф называется помеченным. В качестве пометок обычно используются буквы или целые числа.

Если е=(V_i,V_j), то ребро е называется петлей.

Граф G называется простым, если он не содержит кратных ребер и петель.

Граф G является графом порядка n, если множество его вершин состоит из n элементов, т.е. . Граф, не имеющий ребер, называется пустым. Граф, не имеющий вершин называется нуль-графом.

Граф G называется связным, если в нем существует путь между каждой парой вершин.

Если граф является связным, тот он имеет только одну компоненту связности – сам граф G.

Специальные графы.

1. Полным графом называется граф, без крайних ребер и петель, у которого каждые две вершины смежны. Обозначается K_n. Пусть задан граф G=(V,E,φ).

Граф называется однородным, если все вершины имеют одинаковую степень, . Очевидно, полный граф является (n-1) однородным.

1 – однородный граф называется паросочетанием;

3 – однородный граф называется кубическим.

2. Граф G=(V,E,φ) называется двудольным, если множество его вершин можно разбить на непересекающиеся подмножества V₁ и V₂, а ребра связывают вершины из разных подмножеств.

Полным двудольным графом называется граф, у которого 1) , ; 2) для каждой вершины и существует ребро .

3. Двойственные графы – если между ребрами графов взаимооднозначные соответствия, то такое подмножество графа G (ребер) образующих цикл в графе G соответствует подмножеству ребер G*, образующих разрез в графе G*.

4. Планерный граф – граф, который можно изобразить на плоскости так, что его ребра пересекаются только в вершинах.

Эйлеровы графы.

Эйлеровой цепью в графе G называется замкнутая цепь, содержащая все ребра графа G.

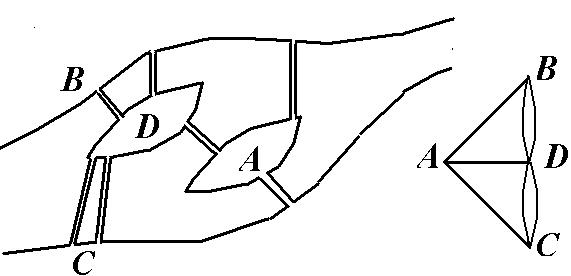
Открытая эйлерова цепь – открытая цепь графа G, содержащая все его ребра. Граф, содержащий эйлерову цепь, называется Эйлеровым.

Теорема 1: Граф G является эйлеровым тогда и только тогда, когда степень каждой вершины четная.

Теорема 2: Граф G является эйлеровым тогда и только тогда, когда он является объединением нескольких реберно-непересекающихся циклов.

Эти условия являются необходимыми и достаточными для определения эйлеровых графов.

Гамильтоновы графы.

Г

амильтоновым циклом в графе G называется цикл, содержащий все вершины графа G.

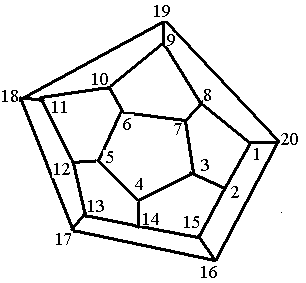
Гамильтонов путь – это путь, содержащий все вершины графа G.

Одна из нерешенных проблем теории графов – это выработка необходимого условия. Однако известно несколько достоверных условий.

: Простой граф является гамильтоновым, если 1) степени вершин обладают последовательность ; 2) .