6. Оптимальное кодирование информации.

Пусть имеется дискретный ансамбль Х={х, р(х)}, требуется построить неравномерный двоичный код. Причем, необходим такой код, который обладает свойством однозначной декоди-уемости.

Определение: код обладает свойством однозначной декодируемости, если он допускает разделение кодовой последова­тельности на отдельные кодовые слова, без использования ка­ких-либо дополнительных символов.

Пример

Пусть имеется множество Х={ 1,2,3,4}.Кодировать будем с помощью двоичного алфавита А={0,1}.Пусть имеются коды

C₁={00,01,10,11}

С₂={1,01,001,000}

Сз={1,10,100,000}

С₄={0,1,10,01}

Из этих множеств только С4 не обладает свойством декоди­руемоемости. Код С2 из неравномерных кодов наиболее легко рас­шифровывается, т.к. ни одно кодовое слово не является началом другого слова. Такие коды называются префиксными.

Префиксные коды всегда являются однозначно декодируемымы

Префиксность - достаточное, но не необходимое условие декодируемости (например, Сз - код однозначно декодируемый, но не префиксный).

Префиксные коды удобно представить в виде кодовых де­ревьев

Определение: Код называется древовидным, если в каче­стве кодовых слов он содержит только кодовые слова соответст­вующие концевым вершинам дерева.

В дальнейшем будем рассматривать только префиксные.

При сравнении кодов логично в качестве критерия выбрать среднюю длину кодового слова.

Определение: Пусть имеется дискретный ансамбль Х={х,р(х)} и пусть для его кодирования выбран код с= {С₁,C₂,...,C_m}. Обозначим через l_i длину i-гo кодового слова. Тогда средняя длина кодового слова:

lcp=M[l(x)]=∑l_i *p(X_i)

Сравним среднюю длину кодовых слов для рассмотренного примера. Будем считать, что вероятности появления кодовых слов равны.

Код С1 является равномерным 1_ср=2.

Код С₂ является неравномерным lc_P=2,25.

Код С_з также не является равномерным 1_ср=2,25.

Первый аспект: не всегда и не любой неравномерный код будет более эффективным. Однако, если бы короткие слова имели более высокую вероятность появления, то средняя длина кодового слова была бы меньше. Если вероятность появления кодовых слов неодинакова, то неравномерные коды более эф­фективны и дают меньшую среднюю длину.

Второй аспект при сравнения кодов - сложность реализа­ции кодирования.

Причем, сложность зависит от области применения. Если кодирование реализуется на универсальном компьютере, то оперативная память неограниченна. Если код реализован на ин­тегральной схеме, то память является определяющим фактором.

Кроме того, коды часто являются составной частью более сложного алгоритма, поэтому имеет значение сложность моди­фикации кода, при изменении статических данных об источнике.

Таким образом, задача неравномерного кодирования есть построение однозначного кода с наименьшей длинной кодового слова, при заданных ограничениях на сложность.

Принципы построения оптимальных неравномерных кодов:

1. Каждый элементарный символ должен переносить максимальное количество информации. Для этого нули и единицы должны встречаться в закодированном тексте приблизительно в равном количестве.

2. Буквы, имеющие наибольшую вероятность, должны ко­дироваться более короткими словами.

Первый оптимальный код - код Шеннона-Фано имеет следующий алгоритм:

Шаг 1. Все вероятности сортируются в порядке убывания.

Шаг 2. Все сообщения разбивают на две группы так, чтобы суммарные вероятности группы были приблизительно равными. Первой группе присваиваем ноль, а второй единицу.

Шаг 3. Если в подгруппе количество символов больше единицы, то переходим к шагу два. Если во всех группах сооб­щений по одному, то построение кодов закончено.

Второй оптимальный код - код Хаффмана. Код Хаффмана строится следующим образом:

Шаг 1. Буквы располагают в порядке убывания вероятностей

Шаг 2. Складывают вероятности двух последних букв.

Шаг 3. Ряд переписывают с учетом новой суммарной веро­ятности. Эти действия повторяют пока суммарная вероятность не станет равной единице.

Чтобы не упорядочивать вероятности для построения кода Хаффмана используют следующий алгоритм:

1. Инициализация. Список подлежащих обработке слов состоит из М=0 узлов, каждому из которых предписана некоторая вероятность.

2. Организуем цикл пока М>1.

Находим два узла с наименьшими вероятностями, ис­ключаем их из списка.

Вместо них вводим новый узел, вероятность которого равна сумме исключенных узлов.

Новый узел связывается ребрами с исключенными уз­лами. Уменьшаем М=М-1. В результате получится кодовое дерево. Существует совмещенной способ построения кода Хаффмана:

Пусть имеется пять символов, которые имеют заданные ве­роятности. Соответствующее дерево кода Хаффмана будет иметь вид: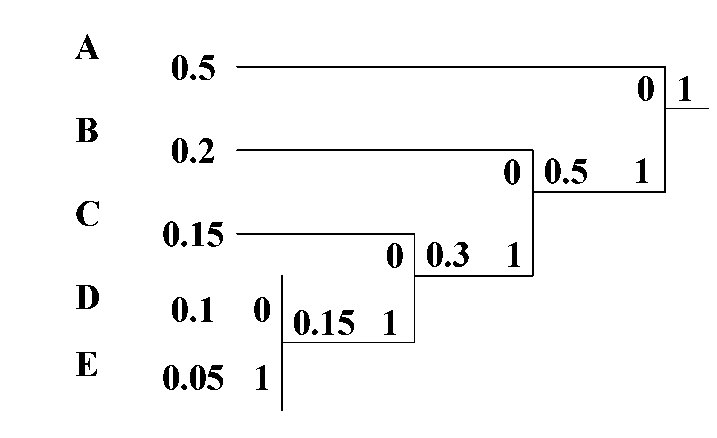

Достоинство кода Хаффмана в том, что можно использо­вать не только двоичные алфавиты.

Свойства оптимальных кодов:

1. Если все сообщения равновероятны, то оптимальным будет равномерный код. При этом, если количество сообщений равно целой степени двойки, то средняя длина кодового слова будет равна энтропии.

2. Слова с одинаковой вероятностью имеют одинаковую длину

3) Кодовые слова с наименьшей вероятностью имеют наибольшую длину.

4) Если кодовый алфавит состоит из к символов, тогда средняя длина кодового слова l_cp=H/log₂K.

5) Можно рассчитать коэффициент сжатия кода

µ=H_max/(l_cp*log₂K) Для двоичных кодов µ=H_max/l_cp

Коэффициент относительной эффективности кода К_оэ= H/(l_cP*log₂K).