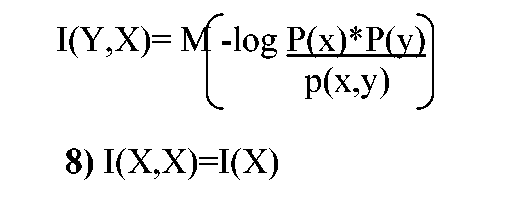1 Простое объединение

Корневую вершину одного дерева делаем сыном корня другого дерева.

Чаще решается задача объединения множеств к которым принадлежат некоторые элементы х и у.

1. Находим корни соответствующих множеств

2. Проверяем, не совпадают ли найденные корни. Если да, то задача решена, если нет, то присоединяем корень одного дерева к другому.

2 Объединение по размерам

В этом случае корень дерева большего размера будем счи­тать отцом корня дерева меньшего размера. Размер дерева это количество вершин дерева. Здесь надо хранить информацию о размере дерева. Размер хранится в виде отрицательных чисел в корневых вершинах.

3 Объединение по высоте

Вместо размера дерева в корне хранится высота. При объе­динении корень дерева с меньшей высотой становится сыном корня дерева с большей высотой.

8 Бинарные кучи

Бинарные кучи используются для организации приоритетных очередей. Элементы поступают в строгом порядке, а поки­дают очередь по значению некоторого ключа приоритета. Чаще всего в качестве приоритета используется оставшееся время ожидания. Чем меньше оставшееся время ожидания, тем выше приоритет.

Бинарная куча - это полное бинарное дерево, для которого выполняется следующее условие- приоритет любой вершины не ниже приоритета ее сыновей.

Организуются полные бинарные деревья в виде одномерного массива.

При выполнении операций с бинарными кучами это свой­ство надо сохранять.

3. Понятие кода и способы его задания.

Кодирование – преобразование символов одного алфавита в символы другого.

Исходный авфавит наз. Первичным алфавит, в который преобразуют символы первичного алфавита в код наз. Вторичным или кодовым.

Код – совокупность знаков и система правил, в соответствии с которыми осуществляется преобразование сообщения из одного вида в другой для передачи, обработки и хранения информации.

Кодовое слово – последовательность знаков кодового алфавита, отображающая некоторое сообщение. Весь набор кодовых слов образует кодовое множество. Различают равномерное и неравномерное коды.

Равномерный код – если длинна кодового слова постоянна.

Мощность кода – число кодовых слов в кодовом множестве.

Кодовое множество называется полным, если в нем представлены все кодовые слова, которые можно получить из кодового алфавита.

Мощность полного кодового множества для равномерного кода:

M=Kⁿ К- количество символов кодового алфавита, n-длина кодового слова

Выделяют основные способы задания кодов.

1. Перечисление кодовых слов

2. Геометрический (код представляется в виде геометрической фигуры или ее развертки)

Это представление чаще всего используется для удобства анализов свойств кода.

3. Кодовое дерево или граф.

Кодовыми словами являются концевые вершины.

Слово получается движением от корня к концевой вершине.

4. Матричный.

В этом случае задается базисная матрица, которая является порождающей для кода. Используется для помехоустойчивого кодирования.

4. Понятие о количестве информации.

Пусть требуется передать позицию шахматной фигуры.

Предположим, для передачи используется двоичный алфавит. Тогда:

- Количество информации не зависит от способа передачи

- Длина сообщения зависит от количества знаков кодового алфавита, но количество информации от этого не зависит.

- Количество информации зависит от числа сообщений, если каждое сообщение устраняет неизвестность о передаваемом факте.

Пусть количество знаков кодового алфавита = m, а длинна кодового слова =n/

Количество сообщение, которое можно передать: N=mⁿ

Это число хотели выбрать в качестве меры, но это число слишком быстро растет при увеличении длинны кодового слова. Поэтому Хартли предложил в качестве меры взять логарифм этого числа:

I=logN=logmⁿ=nLogm – ф-ла Харли.

Основание логарифма определяет единицу измерения количества иформации.

2- бит; 10 – дит; 2 – нат.

Формула Харли годится только для равновероятных сообщений.

Собственной информацией сообщения х Є Х наз. Величина I(x)=-logp(x)

(ф-ла Шермана)

Формулы Шермана и Хартли соответствуют друг другу.

Свойства собственной информации.

1. Неотрицательность I(x)≥0 xЄX. Равенство 0 имеет место только если p=1

2. Монотонность. Для любых х₁, х₂ Є Х, если р(х₁)≥р(х₂), то I(x₁)≤I(x₂)

3. Удитивность. Для любых х₁, х₂ Є Х I(х₁…x_в)=∑I(x_i)

Количество информации в сложной системе

Пусть имеется дискретный ансамбль Х={х,р(х)}. Среднее ожидаемое количество информации для системы X характери­зуется величиной энтропии Н(х). Однако, если наблюдение за системой X ведется через систему Y возникает вопрос: «Как определить количество информации?»

Количество информации, содержащийся в сообщении сис­темы Y относительно сообщений системы X, будет равно коли­честву информации, передаваемой из X.

X — потери, вызванные действием помех.

Определение: Полная информация о системе X, получен­ная через систему Y, определяется величиной I(Y,X)=H(X) -H(X/Y).

Свойства полной информации:

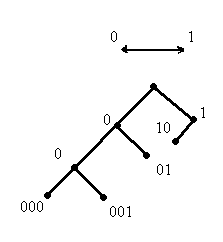
1)Симметричность: I(Y,X)=I(X,Y).

Каждая из двух систем содержит относительно друг друга одну и туже информацию.

2. Неотрицательность: I(Y/X)>0

3. Полная информация I(Y/X)=0, когда системы X и Y не­зависимы.

4. Если системы X и Y эквивалентны, то I(Y,X)=I(Y)=I(X).

5) Если Y- система, подчиненная системе X, то I(Y,X)=H(Y).

6. Для определения полной информации можно использо­вать следующую формулу: I(Y/X)=H(X)+H(Y)-H(X,Y)

7. Полную информацию можно выразить через математи­ческое ожидание: