1. Постановка задачи линейного программирования. ОПЕРАЦИЕЙ называется всякое мероприятие, объединенное единым замыслом и направленное на достижение вполне определенной цели, если существуют различные пути для достижения одной и той же цели, то желательно идти наилучшим из них. Всякий определенный выбор зависящих от нас параметров называется РЕШЕНИЕМ. Если для решения используется тот или иной математический аппарата, то говорят об ИССЛЕДОВАНИИ ОПЕРАЦИЙ. Цель исследования операций – предварительное количественное обоснование решения.

Задачи исследования операций делятся на 2 КАТЕГОРИИ: прямые и обратные.

ПРЯМАЯ задача – отвечает на вопрос, что будет, если в заданных условиях принято указанное решение. Для решения такой задачи нужна модель, позволяющая выразить один или несколько критериев через заданные условия.

ОБРАТНАЯ задача – отвечает на вопрос, как выбрать решение для того, чтобы обратить критерий эффективности в экстремум. Для решения обратной задачи нужно уметь решать прямую задачу. В основу классификации задач обычно закладывается вид функций критерия эффективности и условий. В связи с этим задачи делятся на 2 КЛАССА:

• линейные (все переменные входят в линейной связи);

• нелинейные.

Наиболее широкое применение находят задачи линейного программирования, представляющие собой подкласс задач поиска оптимума с дополнительными условиями в форме неравенств.

Линейные задачи обладают следующими свойствами: пропорциональность и аддитивность.

1. Пропорциональность – вклад каждой переменной в целевую функцию и общий объем потребления соответствующих ресурсов прямо пропорционален уровню (величине) этой переменной.

2. Аддитивность – заключается в том, что целевая функция представляет собой сумму вкладов от различных переменных. В общем случае линейная задача записывается так:

«развернутая форма» записи:

дана целевая функция: Z = ∑ C_i x_i

заданы ограничения: ∑_j a_ij x_j ≤ b_i

V x_i ≥ 0.

«матричная форма» записи: Z = CX

AX ≤ B

X ≥ 0

«каноническая форма» записи: ┌ ┐

│ Z = CX │

│ AX = B │

│ X ≥ 0 │

└ ┘

Сведение к форме равенств (как в канонической форме) требует введения дополнительных переменных. Это увеличивает размерность задачи, но часто является единственным путем решения.

Общие свойства таких задач следующие:

1. Экстремум целевой функции, если существует, всегда абсолютен.

2. Решение задачи, согласно правилу Парето, находится в крайних точках многогранника решений.

Способ перехода от одной крайней точки к другой в поисках оптимального решения обычно и называется методом линейного программирования.

Построение математической модели:

Процесс построения математической модели для решения некой поставленной задачи можно начать с ответов на три следующие вопроса:

1. Для определения каких величин должна быть построена модель? Другими словами, как идентифицировать переменные (искомые величины) задачи?

2. Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, характерные для моделируемой системы?

3. В чем состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному (наилучшему) решению задачи?

Трудность построения математической модели заключается в идентификации переменных и последующем представлении цели и ограничений в виде математических функций этих переменных.

Допустим модель построена, как же определить линейный характер построенной модели? С формальных позиций построенная модель является линейной потому, что все входящие в нее функции (ограничения и целевая функция) линейны. Линейность предполагает наличие двух свойств - пропорциональности и аддитивности, о которых говорилось выше.

2. Геометрическая интерпретация задачи линейного программирования. Для представления на плоскости нужно разрешить все уравнения задачи линейного программирования относительно двух переменных. Если это удается, то можно провести геометрическое решение (поскольку только в этом случае можно изобразить на плоскости в 2-х осях координат).

Порядок действий:

1. для каждого из ограничений задачи:

• строится прямая, соответствующая уравнению ограничения;

• исходя из условия неравенства рассматриваемого ограничения заштриховывается область решений этого неравенства.

2) перекрытие штриховок всех ограничений образует многоугольник ОДР (ОДР - область допустимых решений) !!! Если штриховка где-то не перекрывается – решения нет !!!

3) по произвольным точкам строится прямая, соответствующая целевой функции.

Определяется направление перемещения, в котором ее значения возрастают (если ищется max) или убывают (при поиске min). В этом направлении осуществляется ее параллельный перенос до тех пор, пока целевая функция не пересечет крайнюю из точек многоугольника решений.

Координаты этой крайней точки и являются оптимальным решением.

РЕШЕНИЕ НА ЧУВСТВИТЕЛЬНОСТЬ

После получения оптимального решения необходимо установить, до каких пор решение будет оставаться в той же точке при изменении коэффициентов целевой функции или изменении ограничивающих условий.

ПЕРВАЯ задача анализа на чувствительность связана с анализом ограничений.

Различают ограничения:

• связывающие (активные) – их прямые проходят через оптимальную точку. Ресурсы, соответствующие связывающим ограничениям, называются ДЕФИЦИТНЫЕ.

• не связывающие – их ресурсы НЕДЕФИЦИТНЫЕ.

Как правило, в задаче на максимум дефицитные ресурсы должны увеличиваться, а недефицитные – уменьшатся.

Предельные границы этих изменений определяются так, чтобы точка исходного решения не менялась (то есть, КООРДИНАТЫ оптимального решения МОГУТ ИЗМЕНЯТСЯ, НО должны ОСТАВАТЬСЯ ПЕРЕСЕЧЕНИЕМ ТЕХ ЖЕ ПРЯМЫХ – решение не должно переходить в другую крайнюю точку).

Результаты анализа обычно сводятся в таблицу со следующими полями:

имя поля	Ресурс	Тип	deltaресурса	deltaZ (целевой функции)	Ценность
значение	i	дефицитный/ недефицитный	± число	Zi-Z0	delta Z . deltaресурса

Ценность ресурса – относительное приращение целевой функции – показывает, изменение объема какого из ДЕФИЦИТНЫХ ресурсов предпочтительнее.

ВТОРАЯ задача – определение изменения коэффициентов целевой функции.

Здесь решается два вопроса:

1. каков возможный диапазон изменений того или иного коэффициента.

2. насколько нужно изменить тот или иной коэффициент, чтобы сделать дефицитный ресурс недефицитным или наоборот.

Решение первого из этих вопросов достигается вращением целевой функции за счет изменения ее коэффициентов так, чтобы решение оставалось в той же точке

(из геометрии: уравнение прямой y = kx+b, где k определяет угол наклона прямой к осям координат).

Вращение функции, вызывающее переход решения в другие крайние точки позволяет получить ответ на второй вопрос.

Здесь следует отметить: если модель содержит только две переменные, задачу можно решить графически. В случае трех переменных графическое решение задач становится менее наглядным, а при большем числе переменных – даже невозможным.

Пример: max z=3 хЕ +2 xI | (целевая функция)

при хЕ +2 xI <= 6 |

2 хЕ + xI <=8 |

- хЕ + xI <= 1 | (ограничения).

xI <=2 |

хЕ <=0 xI <=0 |

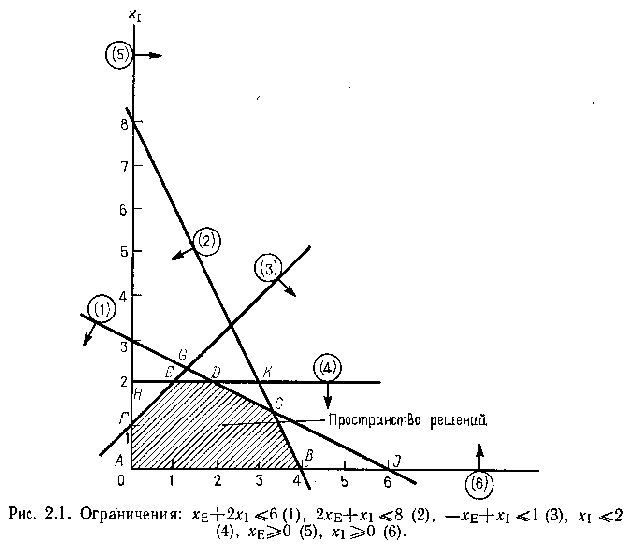
Первый шаг при использовании графического метода заключается в геометрическом представлении допустимых решений, т. е. построении области (допустимых) решений, в которой одновременно удовлетворяются все ограничения модели. Искомая область (пространство) решений показана на РИСУНКЕ. Условия неотрицательности переменных хЕ >= 0 и xI >= 0 ограничивают область их допустимых значений первым квадрантом (представляющим собой по определению часть плоскости, расположенную над осью хЕ и правее оси xI). Другие границы пространства решений изображены на плоскости хЕ, хI прямыми линиями, построенными по уравнениям, которые получаются при замене знака <= на знак = в остальных ограничениях. Области, в которых выполняются соответствующие ограничения в виде неравенств, указываются стрелками, направленными в сторону допустимых значений переменных. Полученное таким образом пространство решений - многоугольник ABCDEF - показан на РИСУНКЕ.

В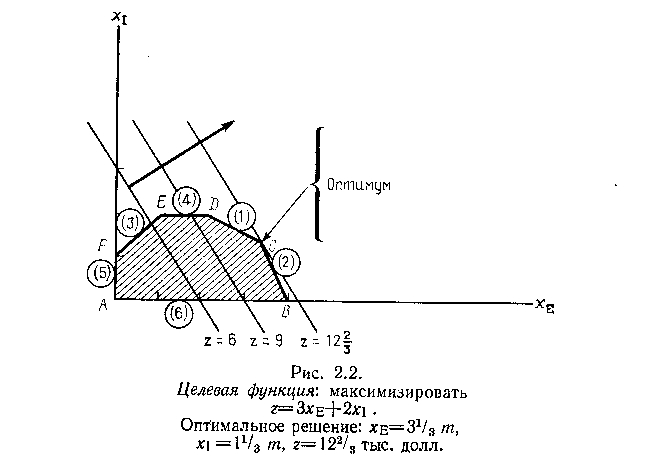каждой точке, принадлежащей внутренней области или границам многоугольника решений ABCDEF, все ограничения выполняются, поэтому решения, соответствующие этим точкам, являются допустимыми. Пространство решений содержит бесконечное число таких точек, но, несмотря на это, можно найти оптимальное решение, если выяснить, в каком направлении возрастает целевая функция моделиz=3 хЕ +2 xI. На РИСУНКЕ ниже показано, как осуществляется такая операция. На график наносят ряд параллельных линий, соответствующих уравнению целевой функции при нескольких произвольно выбранных и последовательно возрастающих значениях z, что позволяет определить наклон целевой функции и направление, в котором происходит ее увеличение (т. е. возрастание общего дохода). На данном РИСУНКЕ использованы следующие значения целевой функции: z=6h z=9.

Чтобы найти оптимальное решение, следует перемещать прямую, характеризующую доход, в направлении возрастания целевой функции до тех пор, пока она не сместится в область недопустимых решений. На РИСУНКЕ видно, что оптимальному решению соответствует точка С. Так как точка С является точкой пересечения прямых (1) и (2) (см. РИСУНОК выше) значения хЕ и хI в этой точке определяются решением следующей системы двух уравнений:

хЕ + xI, = 6,

2 хЕ + xI =8.

Решение указанной системы уравнений дает следующий результат: хE=2, xI=4, Z = 14.

3. Симплекс-алгоритм решения задач линейного программирования.

В вычислительной схеме симплекс-метода реализуется упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки, осуществляется последовательный переход к другой точке (смежной). Выбор каждой последующей точки определяется правилами:

1. каждая последующая угловая точка должна быть смежной предыдущей.

2. Обратный переход к предшествующей точке производиться не может (иначе зацикливание).

Смежные угловые точки отличаются только одной переменной в каждой группе переменных. Эти группы переменных соответственно называются БАЗИСНЫМИ и СВОБОДНЫМИ.

Симплекс-метод требует приведения задачи к стандартному виду, в котором нет ограничений в виде неравенств (все ограничения имеют вид равенств).

Основная Задача Линейного Программирования (ОЗЛП): Z=CX

AX=B

X≥0

!!! В стандартной постановке все bi≥0. К такому виду следует приводить (домножить на -1)

!!! Приведение ограничения к форме равенства достигается путем введения в выражение такого ограничения дополнительной переменной: она прибавляется к левой части, если был знак ≤, и вычитается из левой части, если был знак ≥.

Когда выполняются условия Z=CX, AX=B, X≥0 и bi≥0, то задача задана в канонической форме.

Все условия системы для симплекс-метода надо записать в виде одного уравнения:

Приравниваем уравнения к нулю: Z = CX => CX-Z₀ = 0; AX = B => AX-B = 0, т.е.

C	Z	*	X	= 0
A	B		-1

Матрицу А преобразовать так, чтобы получить единичную матрицу ( I ):

┌ ┐┌ ┐

│ I ^B ││ X │= 0 I X = ^B

│ ││ -1 │

└ ┘└ ┘ C – тоже преобразуется в ^C и ¯C

┌ ┐┌ ┐

│ ^C ¯C ^Z₀ ││ X │= 0,

│ I ¯А ^B ││ -1 │

└ ┘└ ┘то есть векторы С и А разбились каждый на два:

(^C+¯C) X - ^Z₀ = 0

( I+¯A) X - ^B = 0

Переменные, входящие в уравнения:

^C Х - ^Z₀ = 0

I Х - ^B = 0

являются базисными, остальные – свободными. Если в результате построения мы получили все В≥0, то текущее решение является ДОПУСТИМЫМ. Теперь надо определить, нашли ли мы ОПТИМАЛЬНОЕ РЕШЕНИЕ. Если решается задача на min, то оптимум – при всех С≥0, если на max, то при С≤0. Если оптимум не найден, то нужно найти следующую смежную точку: одну из базисных переменных переместить в число свободных, а свободную – в базисные. При этом выбирают ту переменную, которая оказывает максимальное влияние на целевую функцию.

По max ( | ¯с_i | ) выбирается столбец i. А чтобы найти строку j: выбирается min (^b_j/a_i)

На месте разрешающего элемента ij должна стать 1, а остальные значения в этом столбце – обратиться в нуль. Для этого:

1. разрешающая строка нормируется – делиться на значение разрешающего элемента;

2. разрешающий столбец преобразовывается в единичный с единицей в разрешающем элементе (домножением на некоторое число, такое, чтобы последующее сложение с опорной строкой давало 0 в опорном столбце).

После этого делается проверка на выполнение условий достижения оптимума (цикл).

Для отыскания первого опорного решения может быть использовано несколько способов:

1. Введение дополнительных переменных (для приведения неравенств к виду уравнений).

Эти дополнительные переменные собираются во вспомогательную функцию min w = ∑_i x_n+i

Первым шагом решения является минимизация этой функции. После чего дополнительные переменные можно исключить и решать дальше.

2. Метод штрафов

Дополнительные переменные вводятся в систему уравнений ограничений и одновременно в целевую функцию, причем эти переменные вводятся в целевую функцию с такими весовыми коэффициентами Мi, чтобы УХУДШИТЬ целевую функцию. (М отрицательные для поиска max и положительные для поиска min – обычно назначается как максимальный по модулю коэффициент во всех уравнениях, умноженный на 10)

3. Использование свойства двойственности.

Этот метод используется обычно тогда, когда получено опорное решение, но некоторые коэффициенты bi оказались отрицательными. Тогда, если в строке матрицы с этим коэффициентом есть элементы a_ij<0, то решение может быть получено. Иначе – решения нет.

При решении – если коэффициенты уменьшаются по модулю и количество отрицательных элементов уменьшается, то решение будет найдено. Иначе – зацикливание.

ИНТЕРПРЕТАЦИЯ СИМПЛЕКС-ТАБЛИЦЫ

По остаточным переменным определяется статус ресурса: если переменные не находятся в базисе (т.е. = 0) или в базисе, но b=0, то ресурсы – дефицитные. Остальные – недефицитные.

Ценность ресурсов – определяется по строке Z: коэффициенты в этой строке являются коэффициентами ценности ресурса.

Исследование на чувствительность требует перерасчетов: при определении изменения ограничений решение считается остающейся в той же точке, пока коэффициенты bi остаются положительными.

При изменении коэффициентов целевой функции нужно следить за знаком коэффициентов: для min они должны быть все >0 (для max - наоборот).