Изученные теоретические вопросы: Метод ортогонализации

Решение системы уравнений с невырожденной матрицей сводится к нахождению такого вектора, который имеет последнюю координату, равную единице, и ортогонален к линейно независимым векторам.

Применим правило Шмидта для построения ортонормированного базиса пространства, натянутого на заданные линейно независимые векторы. Обозначим через ортогональный базис подпространства, а через- ортонормированный в евклидовой метрике базис того же подпространства. Так как векторынормированы, то их можно представить в виде

, .

На первом шаге метода положим ,.Пусть для некоторого шагауже построен ортогональный базис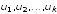и ортонормированный базисподпространства. Векторбудем искать как линейную комбинацию векторов

Условие ортогональности вектора к ортогональным векторамили, что то же самое, к векторамдает. Поэтому

.

Таким образом, с помощью этого итерационного процесса и соотношения строится ортонормированная система векторов . Векторыявляются базисом подпространства. Следовательно, решение исходной системы имеет вид,, гдеи- соответственно-я ия координаты вектора.

Решение:

void main(){

float k,y,q,r,t;

float A[5][5],K[5][5],S[5],B[5][5],X[5],C[5],U[5],V[5][5];

int i,j,j1,jj,n,p,l;

printf("Vvedite razmernost kvadratnoi matricx\n");

scanf("%d",&n);

printf("Vvedite matricix\n");

for(i=0;i<=n;i++)

for(j=0;j<=n;j++)

scanf("%f",&A[i][j]);

for(i=0;i<=n;i++)

for(j=0;j<=n;j++)

K[i][j]=A[i][j];

for(l=0;l<=n;l++)

{

for(i=0;i<=n;i++)

S[i]=K[l][i];

if(l==0)

{

for(i=0;i<=n;i++)

U[i]=S[i];

}

else

{

for(p=0;p<=n;p++)

U[p]=S[p];

for(j1=0;j1<l;j1++)

{

r=0;

for(jj=0;jj<=n;jj++)

r+=S[jj]*B[jj][j1];

C[j1]=-r;

for(jj=0;jj<=n;jj++)

U[jj]+=C[j1]*B[jj][j1];

}

}

r=0;

for(i=0;i<=n;i++)

r+=U[i]*U[i];

q=sqrt(r);

for(i=0;i<=n;i++)

B[i][l]=U[i]/q;

}

for(i=0;i<=n;i++)

B[i][n]=B[i][n]/B[n][n];

for(i=0;i<n;i++)

X[i]=-B[i][n];

printf("poluchennie korni\n");

for(i=0;i<n;i++)

printf("%.2f\n",X[i]);

getch();

}

Результат:

Введенные данные	Полученный результат	Проверка
	2.09 -0.57 0.28	2.7 -1.5 1.2

Лабораторная работа №8

Решить систему методом сопряженных градиентов

Изученные теоретические вопросы: Метод сопряженных градиентов

Метод сопряженных градиентов предназначен для решения систем линейных алгебраических уравнений с симметричной положительно определенной матрицей. Матрица называется положительно определенной, если скалярное произведениедля всех ненулевых векторов. Для того чтобы матрицабыла положительно определенной необходимо и достаточно, чтобы все ее главные миноры были положительны.

Предположим, что заданы два вектора 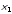и. Последовательные приближенияк решению системы будем строить по формулам

,

,

где

.

Решая систему двух уравнений с двумя неизвестными и, получаем

,

Выберем начальные вектора идля метода сопряженных градиентов. Пусть- произвольный вектор. Построим вектор, где векторвыбирается по направлениютак, чтобы векторыибыли ортогональными, т.е.. Обозначим.

Для выполнения условия ортогональности векторов идостаточно потребовать, чтобы

.

Можно показать, что при таком выборе векторов иитерации метода сопряженных градиентов обрываются не позднее, чем на-ом шаге, давая точное решение системы (- порядок системы).

Решение:

void main() {

int i,j,k=0,n;

float t,tt,t1,e,q,d,z;

float A[10][10];

float Y[10],B[10],X[10],R[10],P[10],U[10];

textcolor(12);

clrscr();

printf("Vvedite razmernost matrix\n");

scanf("%d",&n);

printf("Vvedite matrix\n");

for(i=0; i<n; i++)

for(j=0; j<n; j++)

scanf("%f",&A[i][j]);

printf("Vvedite svobodnie chleni vektora B\n");

for(i=0; i<n; i++)

scanf("%f",&B[i]);

//Проверка матрицы на симметричность

for (i=0; i<n; i++)

for (j=0; j<n; j++)

if (A[i][j]!=A[j][i])

{

printf("\n Matrica ne yavlyaetsya simmetrichnoi!");

getch();

return;

}

X[0]=1;

for (i=1; i<n; i++)

X[i]=0;

i=0;

while (i<n)

{

t=0;

for (j=0; j<n; j++)

{

Y[i]=t+A[i][j]*X[j];

t=Y[i];

}

R[i]=Y[i]-B[i];

i++;

}

t=0;

for (i=0; i<n; i++)

t=t+R[i]*R[i];

i=0;

while (i<n)

{

tt=0;

for (j=0; j<n; j++)

{

Y[i]=tt+A[i][j]*R[j];

tt=Y[i];

}

i++;

}

e=0;

for (i=0; i<n; i++)

e=e+Y[i]*R[i];

q=-t/e;

for (i=0; i<n; i++)

P[i]=q*R[i];

for (i=0; i<n; i++)

X[i]=X[i]+P[i];

k=1;

while (k<n)

{

i=0;

while (i<n)

{

Y[i]=0;

for (j=0; j<n; j++)

Y[i]=Y[i]+A[i][j]*X[j];

R[i]=Y[i]-B[i];

i++;

}

i=0;

while (i<n)

{

t=0;

for (j=0; j<n; j++)

{

Y[i]=t+A[i][j]*R[j];

t=Y[i];

}

i++;

}

i=0;

while (i<n)

{

t=0;

for (j=0; j<n; j++)

{

U[i]=t+A[i][j]*P[j];

t=U[i];

}

i++;

}

t=0;

for (i=0; i<n; i++)

t=t+R[i]*R[i];

tt=0;

for (i=0; i<n; i++)

tt=tt+R[i]*P[i];

t1=0;

for (i=0; i<n; i++)

t1=t1+Y[i]*P[i];

e=0;

for (i=0; i<n; i++)

e=e+Y[i]*R[i];

d=0;

for (i=0; i<n; i++)

d=d+U[i]*P[i];

z=(t*t1-tt*e)/(d*e-t1*t1);

q=(tt*tt-t*d)/(d*e-t1*t1);

for (i=0; i<n; i++)

{

P[i]=z*P[i]+q*R[i];

X[i]=X[i]+P[i];

}

k++;

}

printf("\nkorni\n");

for (i=0; i<n; i++)

printf("%.2f\n",X[i]);

getch();

}

Результат:

Введенные данные	Полученный результат	Проверка
	2.09 -0.57 0.28	2.7 -1.5 1.2