
- •Учреждение образования
- •Лабораторная работа №1 Тема: «Прямые методы решения систем линейных алгебраических уравнений»
- •Изученные теоретические вопросы: Метод Гаусса
- •Решение:
- •Лабораторная работа №2
- •Изученные теоретические вопросы:
- •Лабораторная работа №3
- •Изученные теоретические вопросы:
- •Лабораторная работа №4
- •Изученные теоретические вопросы: Метод квадратного корня
- •Лабораторная работа №5
- •Изученные теоретические вопросы: Метод отражений
- •Лабораторная работа №6 Решить систему линейных алгебраических уравнений методом вращений.
- •Изученные теоретические вопросы:
- •Решение:
- •Лабораторная работа№7 Тема: «Прямые методы решения систем линейных алгебраических уравнений»
- •Изученные теоретические вопросы: Метод ортогонализации
- •Лабораторная работа №8
- •Изученные теоретические вопросы: Метод сопряженных градиентов
- •Лабораторная работа № 9
- •Лабораторная работа № 10
- •Решение:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
«Гомельский государственный университет имени Франциска Скорины»
Математический факультет
ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ АЛГЕБРЫ
Отчет
Выполнил:
студент группы ПМ-21 Кардасёв В.А.
Проверила: Свитич Н.А.
Гомель 2012г
Содержание
Лабораторная работа №1 …………………………………………………………………..3
Лабораторная работа №2 …………………………………………………………………..7
Лабораторная работа №3 …………………………………………………………………..10
Лабораторная работа №4 …………………………………………………………………..13
Лабораторная работа №4 …………………………………………………………………..16
Лабораторная работа №6 …………………………………………………………………..19
Лабораторная работа №7 …………………………………………………………………..22
Лабораторная работа №8 …………………………………………………………………..24
Лабораторная работа №9 …………………………………………………………………..28
Лабораторная работа №10 …………………………………………….………….………..33
Лабораторная работа №1 Тема: «Прямые методы решения систем линейных алгебраических уравнений»
Постановка задачи:
Решить систему линейных алгебраических уравнений:
методом Гаусса по схеме единственного деления;
методом Гаусса с выбором главного элемента.
Найти определитель матрицы
Найти обратную матрицу

Изученные теоретические вопросы: Метод Гаусса
Метод Гаусса и его модификации основаны на приведении с помощью элементарных преобразований исходной системы к системе верхней треугольной или диагональной матрицы. В схеме единственного деления на каждом шаге строка делится на элемент, стоящий на главной диагонали (ведущий элемент), и исключаются элементы под главной диагональю.
После
![]() -го
шага матрица системы принимает вид
-го
шага матрица системы принимает вид
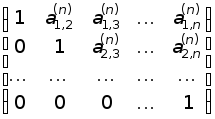 .
.
Процесс приведения матрицы исходной системы к системе с верхней диагональной матрицей называется прямым ходом метода Гаусса, а процесс получения значений неизвестных – обратным ходом. Неизвестные из преобразованной системы находятся по формулам
![]() ,
,
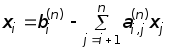 ,
,![]() .
.
Иногда
может оказаться, что система имеет
единственное решение, хотя какой-либо
из главных миноров матрицы
![]() равен нулю. Кроме того, заранее неизвестно,
все ли главные миноры матрицы отличны
от нуля. В этих случаях обычный метод
Гаусса может оказаться непригодным
так, как в процессе вычисления какой-то
ведущий элемент
равен нулю. Кроме того, заранее неизвестно,
все ли главные миноры матрицы отличны
от нуля. В этих случаях обычный метод
Гаусса может оказаться непригодным
так, как в процессе вычисления какой-то
ведущий элемент![]() станет равным нулю. Кроме того, если на
главной диагонали элемент
станет равным нулю. Кроме того, если на
главной диагонали элемент![]() мал, то деление на этот элемент приводит
к значительным ошибкам округления.
Избежать указанных трудностей позволяет
метод Гаусса с выбором главного элемента.
В этом методе исключается не следующее
по порядку неизвестное, а то неизвестное,
коэффициент при котором является
наибольшим по модулю. При применении
такого варианта метода Гаусса не будет
происходить деление на нуль. Различают
три варианта метода Гаусса с выбором
главного элемента:
мал, то деление на этот элемент приводит
к значительным ошибкам округления.
Избежать указанных трудностей позволяет
метод Гаусса с выбором главного элемента.
В этом методе исключается не следующее
по порядку неизвестное, а то неизвестное,
коэффициент при котором является
наибольшим по модулю. При применении
такого варианта метода Гаусса не будет
происходить деление на нуль. Различают
три варианта метода Гаусса с выбором
главного элемента:
а) метод Гаусса с выбором главного элемента по строке: в системе на каждом шаге исключения проводится соответствующая перенумерация переменных;
б) метод Гаусса с выбором главного элемента по столбцу: на каждом шаге исключения проводится перенумерация уравнений;
в) метод Гаусса с выбором главного элемента во всей матрице системы: в этом случае проводится перенумерация и переменных и уравнений.
