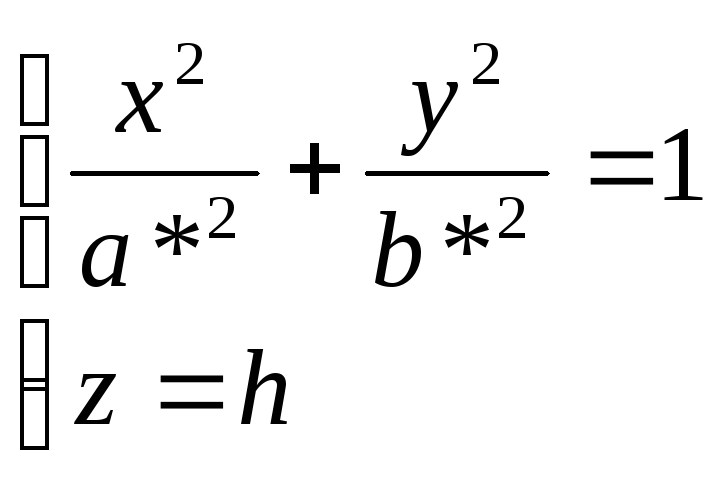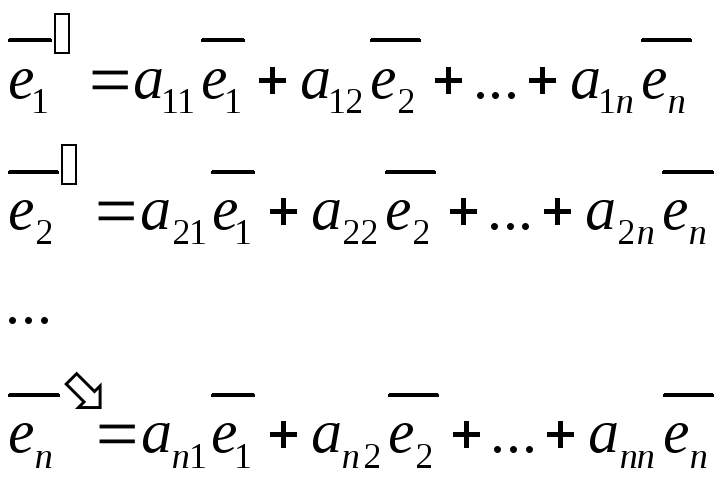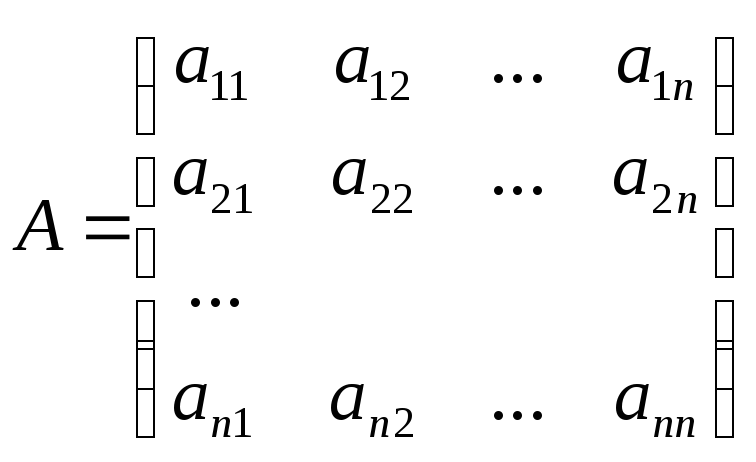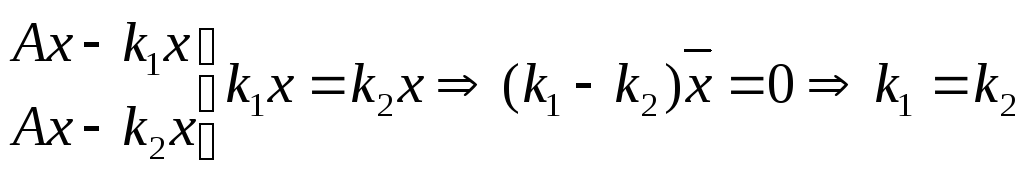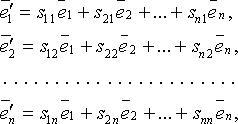шпора Харламова
.doc|
12. Общее уравнение прямой. Всякое уравнение первой степени с двумя неизвестными х и у, т.е. уравнение вида
(где
А, В, С
– постоянные коэффициенты, причем
Частные случаи общего уравнения прямой: 1)
если
2)
если
3)
если
|
|
10
Уравнение
прямой с угловым коэффициентом.
Если в общем уравнении прямой
где
|
|
14.
Уравнение
прямой в отрезках.
Если в общем уравнении прямой
где
|
|
15.
проходит
через точки
где
|
|
18. Нормальное уравнение прямой. Если прямая определяется заданием p и α (рис. 3), то уравнение (7) прямой в прямоугольной системе координат имеет вид
Уравнение (8) можно получить из общего уравнения прямой (1), умножив обе части данного уравнения на нормирующий множитель
учитывая, что знак нормирующего множителя противоположен знаку свободного члена С общего уравнения прямой.
|
|
16.
Угол
между прямыми.
Если прямые
11.
Условие параллельности двух прямых.
Для того чтобы прямые Для
того чтобы прямые 12.
Условие перпендикулярности двух
прямых.
Для того чтобы прямые Для
того чтобы прямые
|
|
21
Уравнение
прямой, проходящей через данную точку
в данном направлении.
Если прямая проходит через точку
5.
Данное
уравнение (4) с различными значениями
коэффициента k
называют
также уравнениями
пучка прямых
с центром в точке
|
|
19.
Расстояние
от точки до прямой.
Если прямая
|
|
22. Общее уравнение плоскости Р имеет вид
где
Частные случаи общего уравнения плоскости:
1.Если
2.Если
C=0,
то имеем уравнение Ax+By+D=0.
Нормальный вектор
3.Если C=D=0, то плоскость проходит через O(0;0;0) параллельно оси Oz, т.е. плоскость Ax+By=0 проходит через ось Oz. Аналогично, уравнениям By+Cz=0 и Ax+Cz=0 отвечают плоскости, проходящие соответственно через оси Ox и Oy.
4.Если
A=B=0,
то уравнение (14) принимает вид Cz
+D=0,
т.е.
5.Если A=B=D=0, то уравнение () примет вид Cz=0, т.е. z=0. Это уравнение плоскости Oxy. Аналогично: y=0 – уравнение плоскости Oxz; x=0 – уравнение плоскости Oyx.
|
|
24.
Уравнение
плоскости, проходящей через три
заданные точки
|
|
25.
Уравнение
плоскости в отрезках.
Если плоскость отсекает на осях Ох,
Оу, Oz
соответственно отрезки a,
b, c (рис.
3), т.е. проходит через точки
Замечание. Уравнением (4) удобно пользоваться при построении плоскостей.
|
|
37
Уравнения прямой в пространстве,
проходящей через две заданные точки
|
|
34. Канонические уравнения прямой
определяют
прямую, проходящую через точку
|
|
35. Параметрические уравнения прямой
|
|
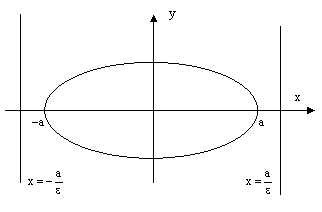
41. Эллипс и его св-ва: Кривая второго порядка наз. эллипсом если коэффициенты А и L имеют одинаковые знаки Аx2+Cy2=
ур.-е
наз.
канонич. ур.-ем эллипса, где
Точки F1(-c,0) и F2(c,0) - наз. фокусами эллипса а. Отношение =с/а наз. его эксцентриситетом (0<=<=1) Точки A1,A2,B1,B2 -вершины эллипса. Св-во: Для любой точки эллипса сумма расстояний этой точки до фокусов есть величина постоянной, =2а.
|
|
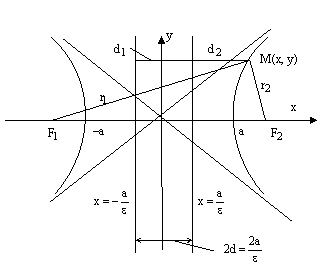
42. Гиперболой называется множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (ее обозначают через 2а), причем эта постоянная меньше расстояния между фокусами. Если
поместить фокусы гиперболы в точках
где
Прямая
называется асимптотой
гиперболы, если расстояние точки
М(х;у)
гиперболы этой прямой стремится к
нулю при
Н
Фокальные
радиус-векторы правой ветви гиперболы:
Фокальные
радиус-векторы левой ветви гиперболы:
|
|
43. Параболой называется множество всех точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Если
директрисой параболы является прямая
Эта
парабола расположена симметрично
относительно оси абсцисс (рис. 8, где
Длина
фокального радиус-вектора параболы
|
|
27. Взаимное расположение плоскостей.
N1,N2-нормальные векторы плоскости. P:A1x+B1y+C1z+D1=0 Q:A2x+B2y+C2z+D2=0 PQ{A1,B1,C1} QN2{A2,B2,C2}
1)Пусть PQ<=>N1N2 A1A2+B1B2+C1C2=0 условие перпендикулярности PQ. 2) Пусть PQ<=> N1N2
A1/A2=B1/B2=C1/C2- Условие параллельности 2х плоскостей. A1/A2=B1/B2=C1/C2=D1/D2- Условие совпадения 2х плоскостей.
|
|
9. Уравнение линии и поверхности. 1. Уравнение сферы. Сфера- геометрическое место точек, равноудаленных от 1ой точки, называемой центром.
|OM|=r, OM={x-a,y-b,z-c}
r2=(x-a)2+(y-b)2+(z-c)2- уравнение сферы. x2+y2+z2=r2- ур-е сферы с центром точке(0,0). F(x,y,z)=0- ур-е поверхности - ур-ю, удовлетворяющему координатам x,y,z любой точки, лежащей на поверхности. 2. Уравнение окружности
r2=(x-a)2+(y-b)2+(z-c)2- ур-е окружности а=b=0, то x2+y2=r2 F(x,y)=0- ур-е линии на плоскости.
|
|
40 Расстояние от точки до прямой на плоскости и до плоскости в пространстве. 1. Ax+By+C=0, M0(x0,y0)
2. Пусть плоскость задана ур-ем Ax+By+Cz+D=0
|
|
46.
Лин простр – множ-во L,эл-ты-ты кот
будем наз век-ми и обозн: a, b, c, .. x, y, z,
на кот опред 2 операции,наз
линейными:1)сложение 2-х век-в(Всяким
2 век-м а,в
V2 – множ-во всех свобод век-в на плоскости с обычн лин операциями V3– множ-во всех свобод век-в в пространстве с обычн лин операциями
М-множ-во всех квадр матриц порядка n Mm*n—множ-во всех матриц размера m*n с обычн лин операциями P С[a,b]- множ-во всех функц,опред и непрерыв на отрезке [a,b]-
Упорядоченная
сист век-в е1,е2 , еn лин прост L наз
базисом в L,если она лнз и если всякий
в-р а
|
|
51. Базисом линейного пространства называется произвольная линейно не зависимая система из n векторов в Rn. Rn – это множество действительных чисел. Если система е1 е2 и тд это система линейно не зависимых векторов в пространстве и любой вектор линейно выразился через данные вектора то пространство является n мерным а вектор е1 еn его базис. 36 Линейное пространство R называется n мерным если в нём существует n линейно независимых векторов, а любые из (n+1) линейно зависимые. Размерность у пространства называется количество в нём линейно независимых векторов. DIM R. Любой вектор x линейного пространства может быть представлен и при том единственным способом в виде линейной комбинации базисных векторов.Если система e1,e2,e3 это система линейно независимых векторов в пространстве и любой вектор линейного выражается через данный вектор , то пространство является n а вектор e1,e2,e3 базис данного векторного линейного пространтва.
|
|
78. Во всяком Евклидовом n мерном пространстве существует ортанормированный базис Переход от одного базиса к другому Переход осуществляется с помощью матрицы перехода.
имеет
координаты
|
|
74.
Нормой
вектора x
называют число, обозначаемое символом
|x|
Свойства
|
|
77.
Угол
между векторами
Два вектора называются ортоганальными если угол между ними 90.Нулевой вектор ортоганален любому.
|
|
|
|
|
|
83. Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
(1)
Уравнение (1) называется каноническим уравнением эллипсоида. Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких плоскостей определяется уравнением вида z=h, где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями
Исследуем уравнения (2) при различных значениях h.
откуда
следует, что плоскость z=h
пересекает
эллипсоид по эллипсу с полуосями
Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz. Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рис. 156). Величины a, b, c называются полуосями эллипсоида. В случае a=b=c эллипсоид является сферой. Однополосный гиперболоид.
Уравнение (3) называется каноническим уравнением однополосного гиперболоида. Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy (y=0) и Oyx (x=0). Получаем соответственно уравнения
из которых следует, что в сечениях получаются гиперболы. Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями
из
которых следует, что плоскость z=h
пересекает гиперболоид по эллипсу с
полуосями
достигающими
своих наименьших значений при h=0,
т.е. в сечении данного гиперболоида
координатной осью Oxy
получается самый маленький эллипс с
полуосями a*=a
и b*=b.
При бесконечном возрастании
Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy. Величины a, b, c называются полуосями однополосного гиперболоида.
Уравнение (5) называется каноническим уравнением двуполостного гиперболоида. Установим геометрический вид поверхности (5). Для этого рассмотрим его сечения координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения
из которых следует, что в сечениях получаются гиперболы. Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, полученная в сечении, определяется уравнениями
из
которых следует, что при
При
При
Величина a, b и c называются полуосями двуполостного гиперболоида.
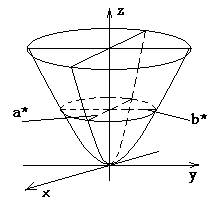
Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
где p>0 и q>0. Уравнение (7) называется каноническим уравнением эллиптического параболоида. Рассмотрим сечения данной поверхности координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения
из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат. Теперь рассмотрим сечения данного параболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями
из
которых следует, что при
Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечно выпуклой чаши. Точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами. В случае p=q уравнение (8) определяет окружность с центром на оси Oz, т.е. эллиптический параболоид можно рассматривать как поверхность, образованную вращением параболы вокруг её оси (параболоид вращения).
Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением
где p>0, q>0. Уравнение (9) называется каноническим уравнением гиперболического параболоида. Рассмотрим сечение параболоида плоскостью Oxz (y=0). Получаем уравнение
из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси Oz, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Oxz (y=h), получаются так же направленные вверх параболы.
рассмотрим сечение данного параболоида плоскостью Oyz (x=0). Получаем уравнение
из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Oz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x=h), получим уравнения
из которых следует, что при любом h в сечении получается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (10). Рассмотрим сечения параболоида плоскостями z=h, параллельными плоскости Oxy . получим уравнения
из которых следует, что при h>0 в сечении получаются гиперболы, пересекающие плоскость Oxy; при h<0 – гиперболы, пересекающие плоскости Oyz; при h=0 – гипербола вырождается в пару пересекающихся прямых
точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами. Конус второго порядка. Конусом второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
Рассмотрим геометрические свойства конуса. В сечение этой поверхности плоскостью Oxy (y=0) получаем линию распадающуюся на две пересекающиеся прямые
Аналогично, в сечении конуса плоскостью Oyz (x=0) также получаются две пересекающиеся прямые
Рассмотрим сечения поверхности плоскостями z=h, параллельными плоскости Oxy. Получим
из
которых следует, что при h>0
и h<0
в сечениях получаются эллипсы с
полуосями
При h=0 линия пересечения поверхности с плоскостью z=h вырождается в точку (0;0;0).
|
|
49-50. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства. Рассмотрим непустое множество элементов, которые будем обозначать через x, y, z, … и множество действительных чисел. На этом множестве введем две операции (сложение и умножение). Пусть эти две операции подчиняются аксиомам:
V;
x,
y,
z,
…
Множество V с двумя операциями, удовлетворяющее аксиомам называется линейным пространством.
Элементы
линейного пространства называются
векторами, обозначаются
Линейная зависимость и независимость системы векторов. Пусть имеется n векторов.
Составим линейную комбинацию:
Если среди n векторов какие-то k линейно-зависимы, то вся система векторов является линейно-зависимой. Если система n векторов линейно-независима, то любая часть из этих векторов будет тоже линейно-независимой. Размерность и базис линейного пространства. Пусть система n векторов линейно-независима, а любая система n+1 векторов – линейно-зависима, тогда число n называют размерностью пространства. dimV=n
Система
этих n
линейно-независимых векторов называется
базисом линейного пространства.
Рассмотрим систему n+1
векторов.
Такое
представление называется разложение
|
|
75. Указанная операция называется скалярным произведением векторов. N – мерное линейное пространство с введенной операцией скалярного произведения, называется Евклидовым пространством. Длиной вектора называется арифметическое значение квадратного корня и скалярного квадрата.
Длина вектора удовлетворяет следующим условиям:
|
|
76.
|
|
73. Скалярное произведение векторов и его свойства. Скалярным произведением двух ненулевых векторов называется число, равное произведению этих векторов на косинус угла между ними.
Рассмотрим линейное пространство V, в котором уже есть 2 операции (сложение и умножение). В этом пространстве введем еще одну операцию. Она будет удовлетворять следующим аксиомам. Указанная операция называется скалярным произведением векторов. N – мерное линейное пространство с введенной операцией скалярного произведения, называется Евклидовым пространством.
|
|
55. Матрица линейного преобразования.
Пусть
F
– линейное преобразование линейного
пространства, переводящая базис
А – является матрицей линейного преобразования или линейным оператором пространства.
|
|
60 Собственные векторы линейного оператора
Ненулевой
вектор
к
– собственное число оператора А=
Каждый собственный вектор имеет единственное собственное число.
|
|
23. 23 Определение. Уравнение
Если
|
|
31. Уравнение пучка плоскостей. Определение. Пучком плоскостей называется множество всех плоскостей пересекающихся по одной и той же прямой, называемой осью пучка.
рис.3. Теорема. Пусть
– две плоскости, пересекающиеся по прямой L. Тогда уравнение
где
Доказательство аналогично доказательству теоремы об уравнении пучка прямых и предоставляется читателю. Пример. Найти уравнение пучка плоскостей, осью которого является ось абсцисс. Решение. Очевидно, что координатные плоскости
рис.4. Тогда уравнение (10) в данном случае принимает вид
где
Аналогично, уравнение
есть уравнение пучка плоскостей с осью пучка Оу, а уравнение
есть уравнение пучка плоскостей с осью пучка Оz.
|
|
32. Уравнение связки плоскостей. Определение. Связкой плоскостей называется множество всех плоскостей, имеющих одну общую точку, которая называется центром связки. Теорема.
Пусть
– три
плоскости
в ПДСК
Охуz, имеющие единственную общую точку
где
Доказательство практически один к одному повторяет доказательство предыдущей теоремы об уравнении пучка прямых. Пример.
Найти уравнение связки плоскостей с
центром связки в точке
Решение.
Очевидно, что следующие три плоскости
пересекаются в единственной точке
Тогда уравнение
где
В
частности, если
есть уравнение связки плоскостей с центром связки в начале координат.
|
|
44. Директрисы эллипса. Определение. Директрисами эллипса называются две прямые, которые в канонической для эллипса системе координат имеют уравнения
рис.8. Теорема.
Пусть М – произвольная точка эллипса,
где
Доказательство.
рис.9. Пусть М(х, у) – координаты произвольной точки эллипса. Тогда
откуда и следуют равенства (14). Теорема доказана. Директрисы гиперболы. Определение. Директрисами гиперболы называются две прямые, уравнения которых в канонической для гиперболы системе координат имеют вид
Так
как
Обозначение. Расстояние между директрисами обозначается 2d и равно
рис.8.
|
|
65.
Определение
квадратичной формы
Квадратичная форма
переменных
Если
переменные
Матрица
называется
матрицей квадратичной формы, ее ранг
- рангом квадратичной формы. Квадратичная
форма называется невырожденной, если
|
|
66. Канонический вид квадратичной формы
Квадратичная
форма называется канонической, если
все
где
2.
Метод Лагранжа
- последовательное выделение полных
квадратов. Например, если
Затем
подобную процедуру проделывают с
квадратичной формой
|
|
70.
Классификация
действительных квадратичных форм
Положительно-определенные
Квадратичные формы,
для которых
Отрицательно-определенные
Квадратичные
формы, для которых
Положительно-полуопределенные
Квадратичные
формы, для которых
Отрицательно-полуопределенные
Квадратичные
формы, для которых
Неопределенные
Квадратичные
формы, которые принимают как
положительные, так и отрицательные
значения. Нормальный вид:
|
|
59.
Матрица
S
перехода от базиса
или
кратко:
Если
|
|
68 Пусть k(x) — квадратичная форма, заданная в пространстве арифметических векторов Rn. В пространстве Rn существует канонический базис квадратичной формы, базис, в котором матрица квадратичной формы является диагональной. В этом базисе квадратичная форма имеет канонический вид k(x) = λ1x12 + λ2x22 + ... + λnxn2. Числа λ1, λ2, ... , λn — канонические коэффициенты квадратичной формы. Закон инерции квадратичных форм гласит: число положительных, отрицательных и нулевых канонических коэфициентов квадратичной формы не зависит от преобразования, с помощью которого квадатичная форма приводится к каноническому виду. Число положительных канонических коэфициентов квадратичной формы называется положительным индексом инерции квадратичной формы. Число отрицательных канонических коэфициентов квадратичной формы называется отрицательным индексом инерции квадратичной формы. Разность между положительным и отрицательным индексами квадратичной формы называется сигнатурой квадратичной формы. Число ненулевых канонических коэффициентов называется рангом квадратичной формы.
|
|
71. Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой. Пусть квадратичная форма имеет в каком-то базисе матрицу
Тогда эта форма положительно определена, если и только если все её главные (угловые) миноры Δi положительны. Форма отрицательно определена, если и только если знаки Δi чередуются, причём Δ1 < 0. Здесь главными минорами матрицы A называются определители вида
Для неотрицательно определённых матриц критерий действует только в одну сторону: если форма неотрицательно определена, то главные миноры неотрицательны. Обратное неверно. Например, матрица
не является неотрицательно определённой — так как, например, (Mv,v) = − 2 для v = (0,1, − 1). В то же время все её главные миноры равны 0, то есть неотрицательны. |
|
1-3. Линейная зависимость векторов. Базис. a1`, a2`,…, an`; Вектора называются линейно-независимыми, если равенство λ1 a1` + λ2 a2` +…+λn an` = 0 выполняется только в тревиальном случае — λ1 a1`+λ2 a2`+…+λn an` = 0, λ1, λ2, λ3…λn=0; и называются линейно-зависимыми, если хотя бы одно из чисел λ <>0;λ1<>0; μ1=λ2/λ1; μ2=λ3/λ2… ; a1`= μ1 a2`+μ2 a3` +…+μ(n - 1) an`; Вектор a1` представлен линейной комбинацией векторов.Докажем следующую ТЕОРЕМУ: Всякие 3 вектора на плоскости линейно зависимые. Дано: a`, b`, c`, причем 2 из них колинеарны. Док-ть: a`=λ1 b`+λ2 c`-?; Док-во: 1) пусть a` и b` колинеарны: a`=λ1 b` + 0 c`; λ1<>0; λ2=0; c`=λ1 a`+λ2 b`=|b`=αa`|=λ1 a`+λ2 α a` = β a` + 0 b`; 2) Дано: a`, b`, c`; c`=λ1 a`+λ2 b`; Док-во: c`=OM`; OM` = OM1`+OM2`; OM1`=λ1 a`; OM2`=λ2 b`; c`=λ1 a` + λ2 b` Следствие: 1. Максимальное число линейно-независимых векторов на плоскости равно двум. 2. Для того, чтобы 2 вектора на плоскости были линейно-независимы <=>, чтобы они были неколлинеарными. |
|
29. Расстояние от точки до плоскости. Дано: M0 (x0;y0;z0)
Расстояние
d
от точки М0
до плоскости ∆ равно модулю проекции
вектора
!!!Если
плоскость задана уравнением: |
|
53. Линейные операции над векторами в координатах.
Пусть заданы векторы в прямоугольной системе координат
Скалярное
произведение векторов. Определение.
Скалярным произведением векторов
Свойства скалярного произведения:
Если
рассматривать векторы
Используя полученные равенства, получаем формулу для вычисления угла между векторами:
|
|
28. Уравнение плоскости по точке и вектору нормали.
Теорема.
Если в пространстве задана точка
М0(х0,
у0,
z0),
то уравнение плоскости, проходящей
через точку М0
перпендикулярно вектору нормали
A(x – x0) + B(y – y0) + C(z – z0) = 0.
Доказательство.
Для произвольной точки М(х, у, z),
принадлежащей плоскости, составим
вектор
Таким образом, получаем уравнение плоскости
Теорема доказана.
|
|
38. Условия параллельности и перпендикулярности прямых в пространстве.
Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.
Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.
|
|
39. Условия параллельности и перпендикулярности прямой и плоскости в пространстве.
Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.
Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарны. Это условие выполняется, если векторное произведение этих векторов было равно нулю.
|
|
47. Свойства линейных пространств.
1) В каждом линейном пространстве существует только один нулевой элемент. 2) Для каждого элемента существует только один противоположный элемент. 3)
Для каждого
4)
Для каждого
R
и
5)
Если 6)
(-1)
|


 . (2)
. (2)
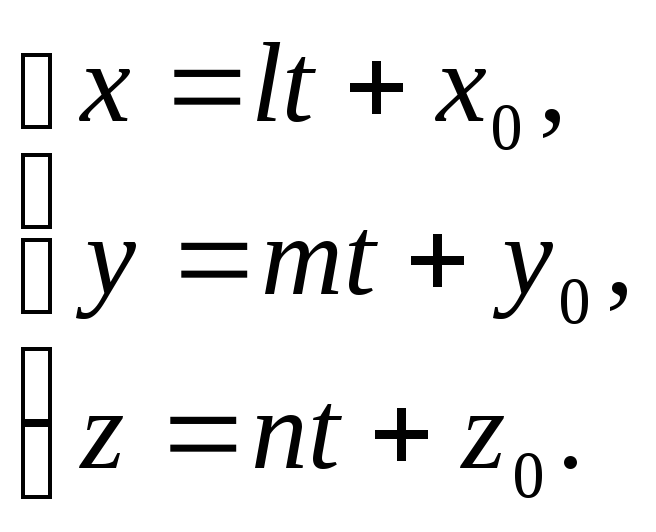
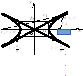 а
рисунке 7 указано взаимное расположение
гиперболы и ее асимптот. Отношение
а
рисунке 7 указано взаимное расположение
гиперболы и ее асимптот. Отношение
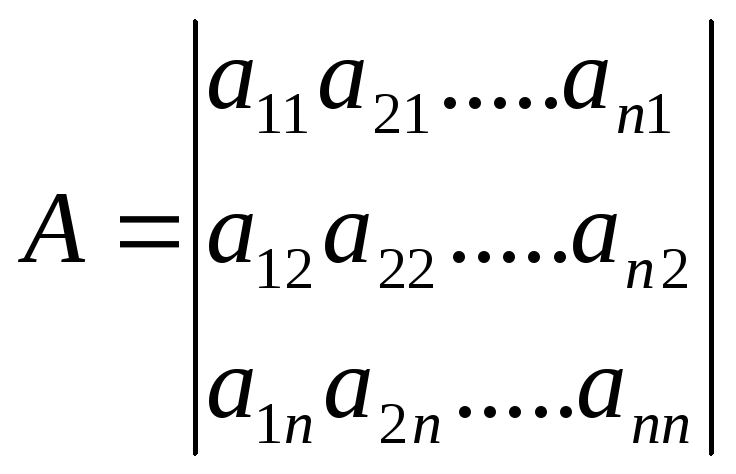 Пусть
x
имеет координаты в старом базисе
Пусть
x
имеет координаты в старом базисе

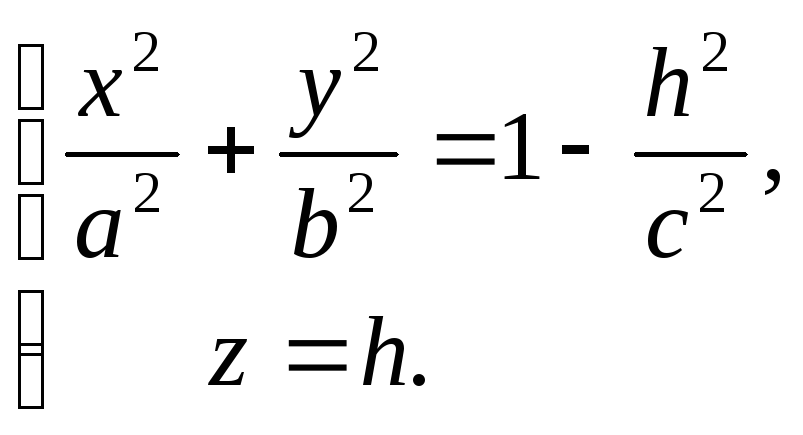 (2)
(2)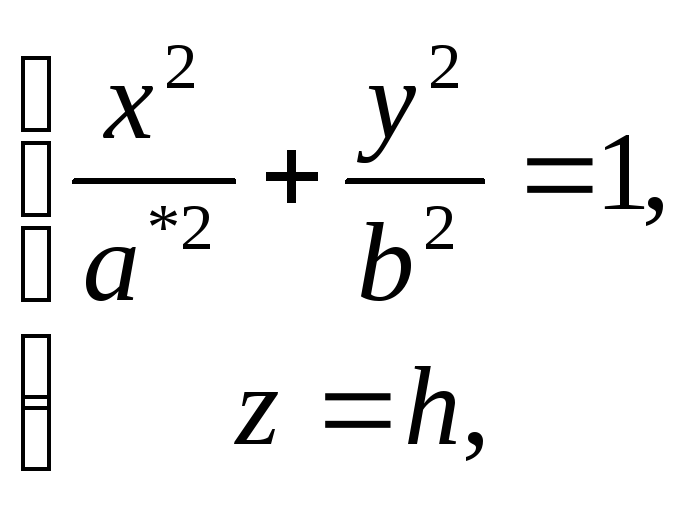
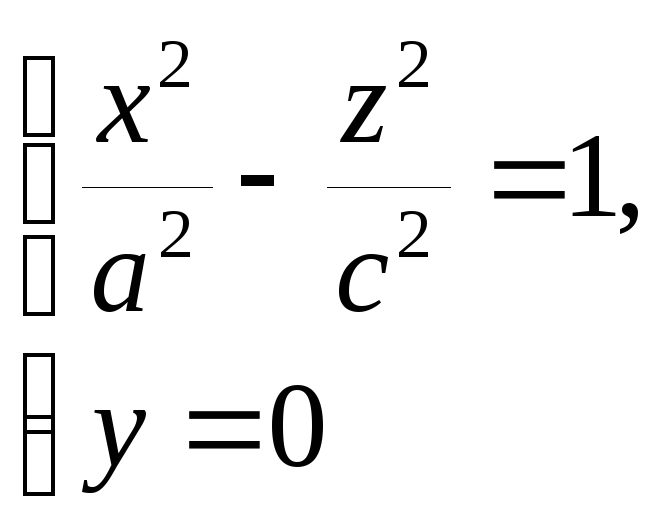 и
и 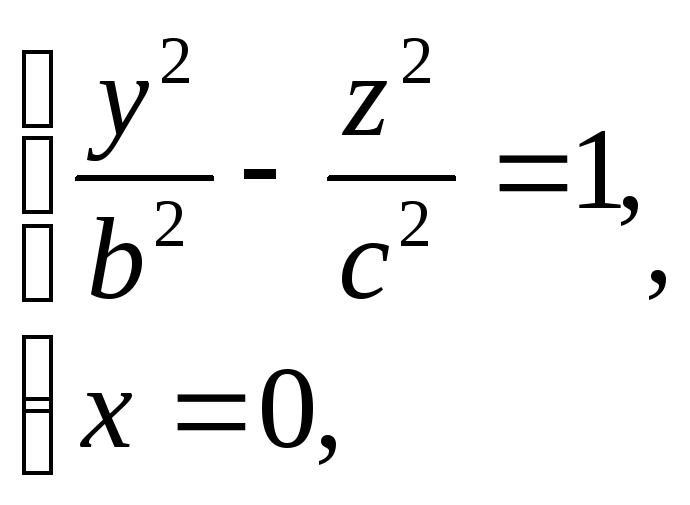
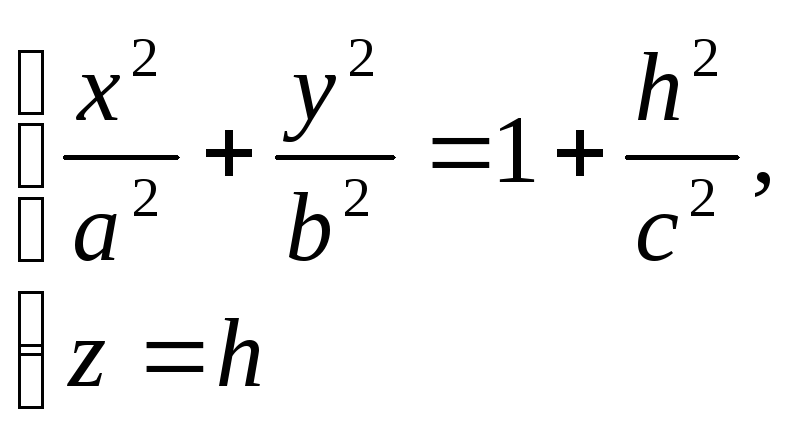 или
или  (4)
(4)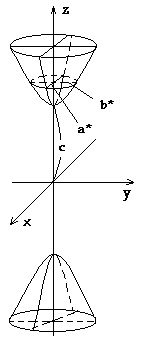 Двуполостным
гиперболоидом называется поверхность,
которая в некоторой прямоугольной
системе координат определяется
уравнением
Двуполостным
гиперболоидом называется поверхность,
которая в некоторой прямоугольной
системе координат определяется
уравнением и
и
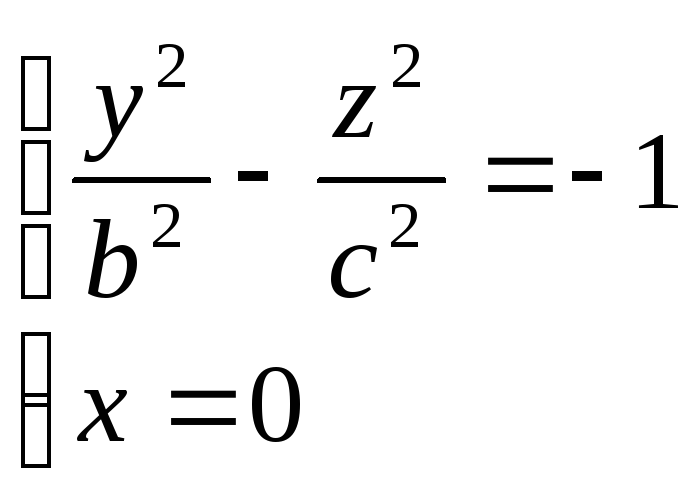
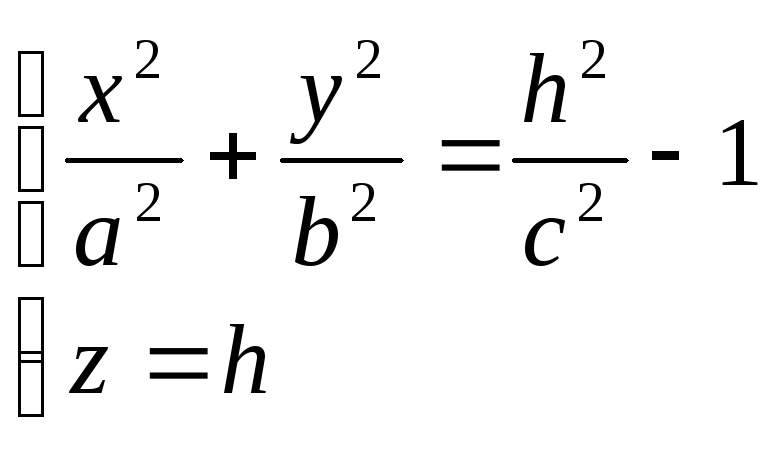 или
или
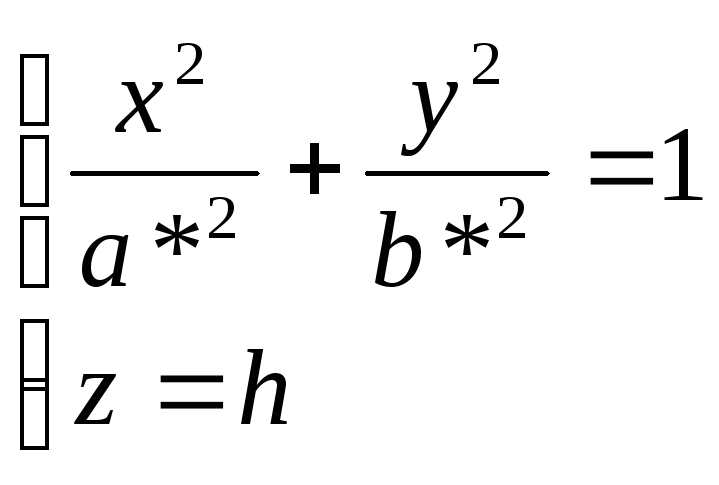 (6)
(6)
 и
и
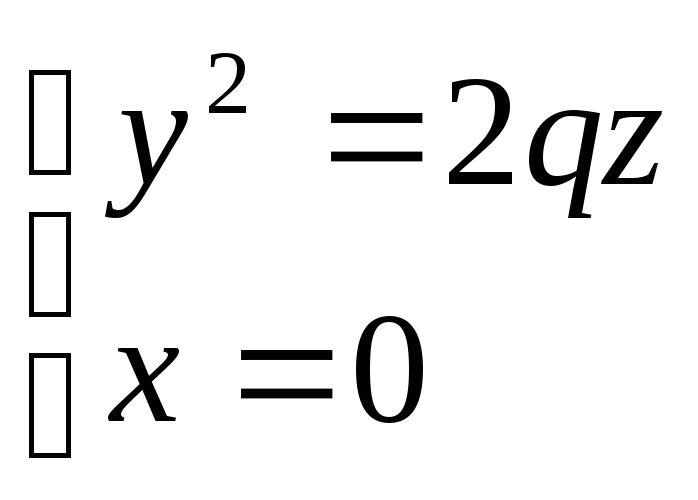
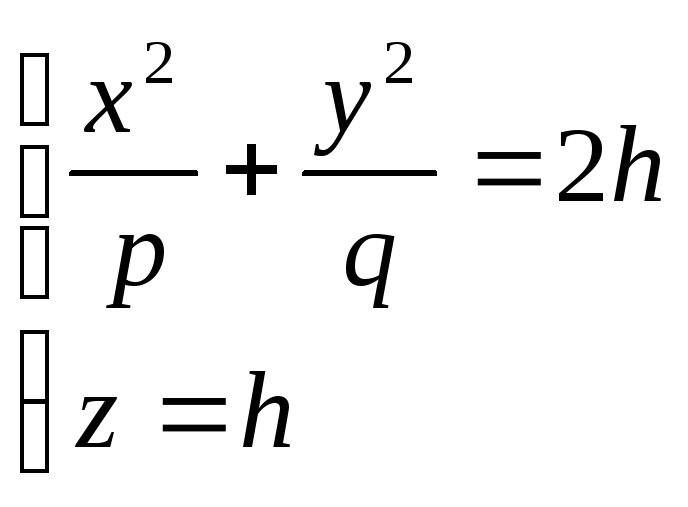 или
или
 (8)
(8)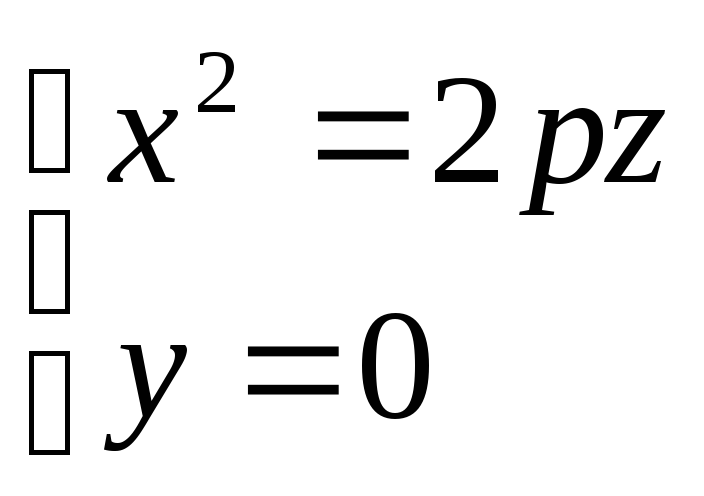 (10)
(10)


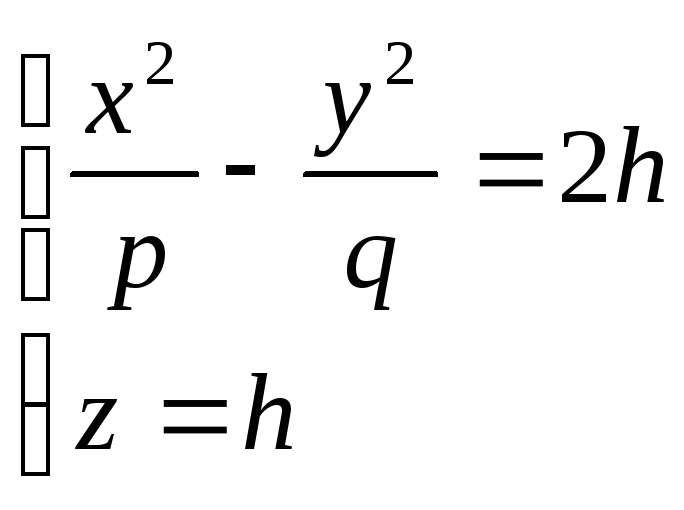 или
или

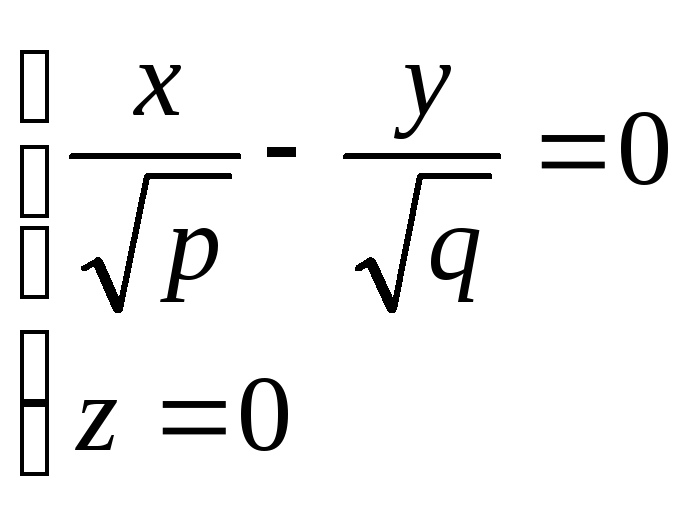 и
и
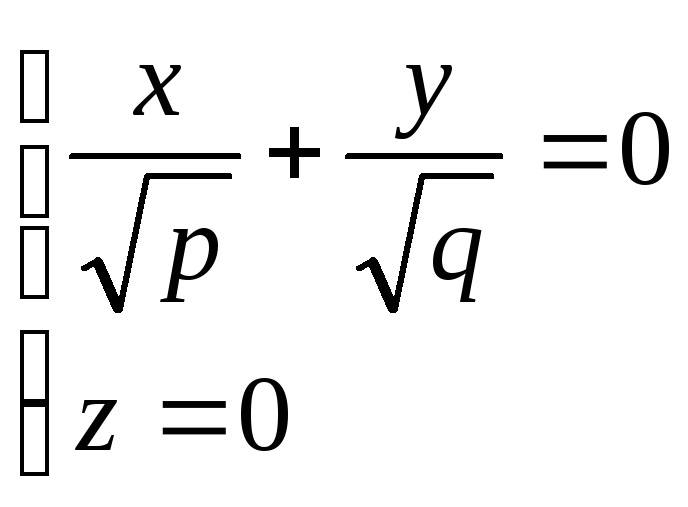

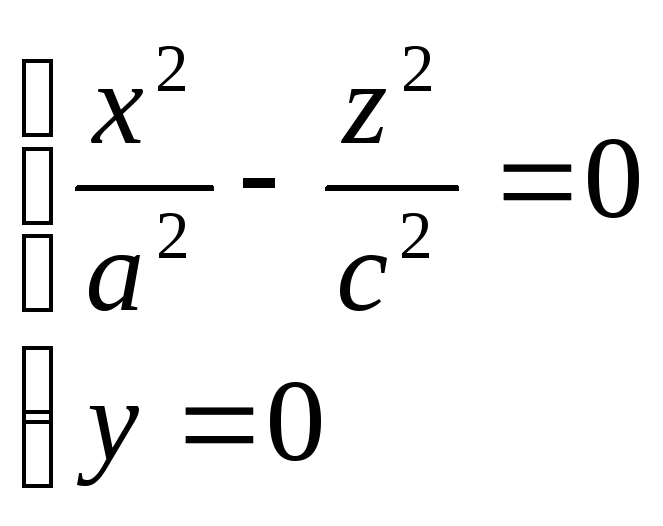
 и
и

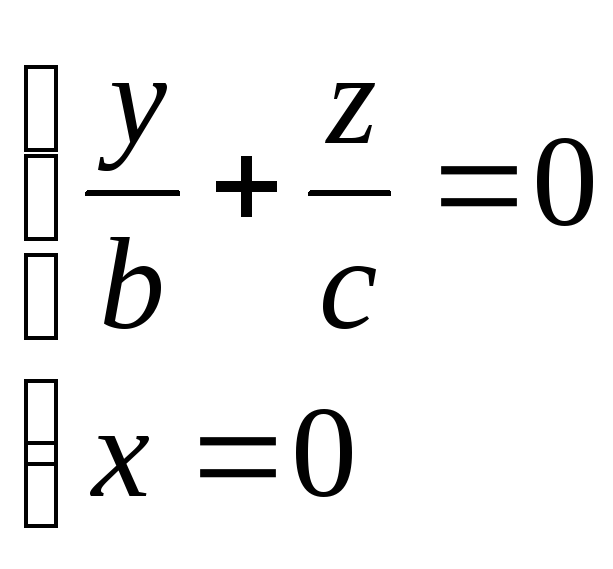 и
и
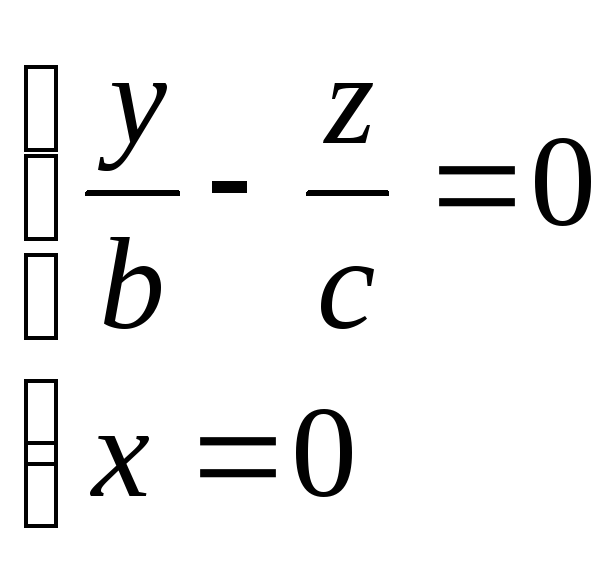
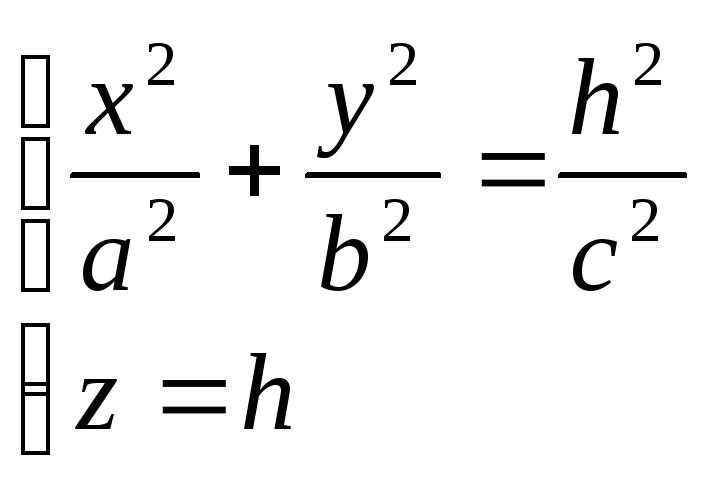 или
или