
Волновая оптика и квантовая физика_2010
.pdf
4.ПОЛЯРИЗАЦИЯ СВЕТА
4.1.Естественный и поляризованный свет
Из теории Максвелла сле- |
|
|
|
||
дует, что свет представляет по- |
|
|
|
||
перечную электромагнитную вол- |
|
|
|
||
ну: векторы напряженностей элек- |
|
|
|
||
трического Е и магнитного H полей |
|
|
|
||
взаимно перпендикулярны и колеб- |
|
|
|
||
лются |
перпендикулярно |
вектору |
а) |
б) |
в) |
распространения волны (см. раздел |
Рис.4.1. Виды света: |
|
|||
1. 3. рис. 1.3). Для описания поля- |
|
||||
ризации достаточно знать поведе- |
а – естественный; |
|
|||
ние лишь одного из векторов. |
б – частично поляризованный; |
||||
Обычно |
таким вектором |
является |
в – поляризованный. |
|
|
световой вектор или вектор напряженности Е электрического поля. Поскольку свет представляет собой совокупность свето- вых волн, излучаемых множеством отдельных атомов, атомы же излучают световые волны независимо друг от друга, в естест- венном луче представлены световые волны со всевозможными равновероятными колебаниями векторов Еi (рис. 4.1 а). Свет, в котором существует преимущественная (но не единственная) ориентация колебаний векторов Еi для всех волн называется
частично поляризованным (рис. 4.1 б). Степень поляризации
света определяется выражением:
Р = I max − I min I max + I min
где Imax –интенсивность колебаний преобладающего направле- ния; Imin - интенсивность колебаний в направлении, перпендику- лярном преобладающему. Для естественного света (Imax = Imin) степень поляризации Р = 0.
41
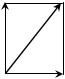
Свет, в котором колебания светового вектора каким-либо образом упорядочены, называется поляризованным (рис. 4.1 в).
Для плоско поляризованного или линейно поляризованного света
(Imin = 0) степень поляризации Р = 1, то есть колебания векторов Еi для всех волн происходят в одной плоскости, называемой
плоскостью поляризации света.
|
|
|
|
Различают три вида поляризации |
Еу |
|
Е |
света: эллиптическую, круговую и плоскую |
|
|
|
|
|
(или линейную). Колебания светового век- |
|
|
|
|
тора Е в любой точке пространства можно |
|
|
|
|
представить результатом сложения двух |
|
|
Ех |
|
взаимно перпендикулярных линейно поля- |
Рис.4.2. Сложение |
ризованных колебаний векторов Ех и Еу |
|||
линейно |
поляри- |
(рис.4.2), которые колеблются по законам |
||
зованных |
колеба- |
Ех = Е0хcos (ωt+ϕ1) |
||
ний |
|
|
|
Еy = Е0ysin (ωt+ϕ2) |
Уравнение траектории результи- рующего вектора Е при сложении взаимно перпендикулярных гармонических колебаний одинаковой частоты имеет следую- щий вид:
Ех2 |
+ |
Еу2 |
− |
2 |
х Еу |
cos(ϕ |
|
− ϕ )= sin2 |
(ϕ |
|
− ϕ ), |
Е02х |
Е02у |
|
|
|
|
||||||
|
|
|
0х Е0 у |
2 |
1 |
|
2 |
1 |
|||
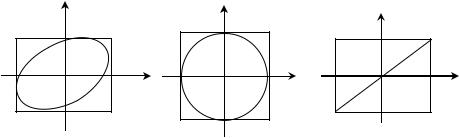
где Е0х и Е0у – амплитуды складываемых колебаний, ϕ2 - ϕ1 – разность фаз колебаний. При произвольном постоянном значе- нии разности фаз траектория, описываемая результирующим вектором Е, является эллипсом (рис.4.3 а), размеры которого за- висят от амплитуд Е0х и Е0у складываемых колебаний и разности их начальных фаз ϕ2 - ϕ1. Такой свет называется эллиптически поляризованным.
Если разность фаз ϕ2 - ϕ1 = (2m+1)π/2, где m = 0,±1, ±2,…,
и амплитуды Е0х = Е0у, то траектория результирующего вектора
42
|
Е |
2 |
+ |
Еу2 |
=1 и представляет собой |
Е описывается уравнением |
|
х |
|
||
2 |
2 |
||||
|
Е0 х |
|
Е0 у |
|
|
окружность (рис.4.3 б), а свет называется поляризованным по кругу (или циклически поляризованным).
При разности фаз ϕ2 - ϕ1 = mπ, где m = 0, ±1, ±2,… эллипс вырождается в отрезок прямой Еу = ±(Е0у /Е0х)Ех (рис. 4.3 в). Та-
кой свет называется линейно поляризованным (плоско поляризо- ванным).
|
у |
у |
|
у |
|
|
|
|
|
||
|
Еу |
Еу |
|
Еу |
|
|
|
Ех |
|
|
Ех |
|
|
|
|
|
|
-Ех |
0 |
х -Ех 0 |
Ех х -Ех |
0 |
х |
|
-Еу |
-Еу |
|
-Еу |
|
|
а) |
|
в) |
|
|
|
б) |
|
|
Рис.4.3. Виды поляризованного света: а – эллиптическая по- ляризация; б – круговая поляризация; в – линейная поляриза- ция.
Свет от естественных источников может приобрести час- тичную или полную поляризацию при взаимодействии с веще- ством. Поляризация света состоит в выделении из светового пучка колебаний определенного направления. Для этой цели ис- пользуют специальные устройства, называемые поляризато- рами. Поляризация света достигается при отражении и прелом- лении на границе раздела двух изотропных диэлектриков, а так- же в результате явления двойного лучепреломления в анизо- тропных кристаллах.
43
4.2. Поляризация света при отражении и преломлении на границе раздела двух изотропных диэлектрических сред.
Оптически изотропная среда (т.е. среда, имеющая оди-
наковые оптические свойства во всех направлениях) представ- ляет собой систему электрических зарядов – ионов и электро- нов, способных совершать колебания под действием электро- магнитных волн. Частота колебаний, соответствующая диапа- зону видимого света, очень большая (ν = 1015 Гц). Поэтому толь- ко заряженные частицы очень маленькой массы могут следовать за изменением поля световой волны. Такими частицами являют- ся электроны. Атомы и их ядра не могут следовать за из- менением этого поля в силу их большой инертной массы. При этом предполагается, что в веществе электроны связаны квази- упругими силами, т.е. являются колебательными системами, ха- рактеризующимися частотой собственных колебаний. Взаимо- действие электронной оболочки атомов с электромагнитным по- лем световой волны приводит к их возбуждению. Возбужденные атомы, приходя в нормальное (невозбужденное) состояние, из- лучают электромагнитные волны, получившие название вто-
ричных волн (или вторичного излучения). Для объяснения обра-
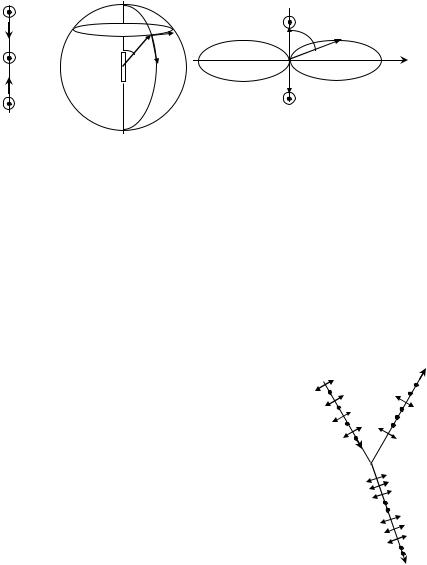
зования и распространения вторичных волн воспользуемся про- стейшей системой, излучающей электромагнитные волны - ко- леблющимся электрическим диполем (рис.4.4 а). Положитель- ный заряд такого диполя сосредоточен в ядре атома, отрица- тельный заряд – электрон – совершает колебания под действием внешнего поля. Если волна распространяется в изотропной сре- де, то волновой фронт будет сферическим (рис.4.4 б). При этом интенсивность вторичных волн зависит от угла θ и поэтому раз- лична в разных направлениях. Зависимость интенсивности от угла наглядно показана на диаграмме направленности излучения диполя (рис.4.4 в). На рисунке 4.4 в видно, что в направлении линии АА' (оси диполя) происходят колебания электрона под действием светового вектора Е поэтому интенсивность
44
-q |
|
|
A' |
|
|
|
|
-q θ |
I(θ) |
+q |
θ |
r |
H |
|
|
E |
X |
||
|
|
|
||
|
|
|
-q |
|
(-q) |
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
а) |
б) |
|
в) |
|
Рис. 4.4 а − электрический диполь; б − образование волнового фронта при распространении в изотропной среде; в − диаграмма направленности излучения ди- поля.
вторичного излучения в этом направлении отсутствует. Интен- сивность максимальна в направлении оси Х, перпендикулярном линии АА'.
Поскольку среднее расстояние между атомами в жидко- стях и твердых телах мало по сравнению с длиной цуга волн
(около 3м), то электронные оболочки |
|
|
||
большого числа |
атомов |
возбуждаются |
|
|
одним цугом волн. Поэтому вторичные |
|
|
||
|
|
|||
волны оказываются когерентными как |
|
|
||
друг с другом, так и с падающей свето- |
|
|
||
вой волной. Эти волны взаимно интер- |
n1 |
|
||
ферируют. Их интерференцией объяс- |
|
|||
n2 |
|
|||
няются явления отражения и преломле- |
|
|
||
ния света в веществе. |
|
|
|
|
При падении естественного света |
|
|
||
на границу раздела двух диэлектриков |
|
|
||
|
|
|||
(например, воздух - стекло) часть его |
Рис.4.5. Поляризация |
|||
отражается, а |
часть |
преломляется |
||
(рис.4.5). При этом оказывается, что от- |
света при отражении |
|||
раженные и преломленные световые лу- |
и преломлении |
|||
|
|
45 |
|
|
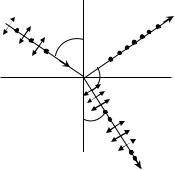
чи частично поляризованы. В отраженном свете преобладают |
||
волны, у которых световой вектор Е колеблется в плоскости, |
||
перпендикулярной плоскости падения (эти колебания вектора Е |
||
изображены точками), а в преломленном свете – в плоскости па- |
||
дения (колебания вектора Е изображены стрелками). |
||
|
Степень поляризации как отраженного, так и преломлен- |
|
|
|
ного света зависит от угла падения |
|
|
и показателей преломления ди- |
|
iБ |
электриков. Шотландский физик |
|
|
Дэвид Брюстер, исследуя поляри- |
n1 |
|
зацию света, установил в1815 г. |
n2 |
ν |
связь между относительным пока- |
|
|
зателем преломления диэлектрика |
|
r |
и углом падения света, при кото- |
|
ром отраженный от поверхности |
|
|
|
|
|
|
свет будет полностью поляризо- |
|
|
ван. Согласно закону Брюстера |
Рис. 4.6. Иллюстрация закона |
при угле падения iБ (угол Брюсте- |
|
Брюстера |
ра), определяемого соотношением |
|
|
|
tg iБ = n21 |
(где n21 – относительный показатель преломления второй среды |
||
относительно первой), отраженный луч будет полностью плос- |
||
ко-поляризован, а преломленный луч – частично поляризован с |
||
максимальной степенью поляризации (рис 4.6). Из данного за- |
||
кона вытекает, что, если свет падает на границу раздела под уг- |
||
лом Брюстера, то отраженный и преломленный лучи взаимно |
||
перпендикулярны. Степень поляризации преломленного света |
||
можно значительно повысить, пропуская свет через устройство, |
||
называемое стопой Столетова (рис.4.7). Стопа Столетова пред- |
||
ставляет собой совокупность одинаковых параллельных друг |
||
другу пластинок из прозрачного диэлектрика (например, стек- |
||
ла). При многократном отражении и преломлении на каждой |
||
|
|
46 |

границе преломленный свет стано- |
|
iБ |
||
вится полностью поляризованным. |
|
|||
|
|
|||
Закон Брюстера можно пояс- |
|
|
||
нить с помощью полярной диаграм- |
|
|
||
мы направленности излучения элек- |
|
|
||
трического диполя (осциллятора). |
|
|
||
Представим |
падающий |
естествен- |
|
|
ный свет как результат сложения |
|
|
||
двух взаимно перпендикулярных ко- |
|
|
||
лебаний (рис.4.8), один световой |
|
|
||
вектор (обозначим его Е||) будет ко- |
Рис. 4.7. Стопа Столетова |
|||
лебаться в плоскости падения (на |
||||
рисунке он показан стрелками), а |
|
|
||
другой (обозначим его Е ) будет колебаться в плоскости, пер- |
||||
пендикулярной плоскости падения (на рис.4.8 он показан точка- |
||||
ми). При прохождении света через вещество под действием век- |
||||
тора Е|| электроны вещества будут совершать вынужденные ко- |
||||
лебания в плоскости падения (эти осцилляторы, оси которых |
||||
лежат в плоскости падения, на преломленном луче обозначены |
||||
стрелками), излучая при этом вто- |
|
|
||
ричные сферические волны. Свето- |
|
iБ |
||
вому вектору Е будут соответство- |
|
|||
вать осцилляторы, оси которых ле- |
n1 |
|
||
жат в перпендикулярной |
плоскости |
|
||
(на преломленном луче они обозна- |
n2 |
π/2 |
||
чены точками). В направлении коле- |
|
|
||
баний электронов излучения вторич- |
|
|
||
ных волн не происходит. При угле |
|
|
||
падения i = iБ отраженный луч пер- |
|
|
||
пендикулярен |
преломленному лучу |
Рис. 4.8. Иллюстрация по- |
||
и, следовательно, параллелен осцил- |
ляризации света при отра- |
|||
ляторам, оси которых расположены в |
жении и преломлении |
|||
плоскости падения, поэтому эти ос- |
|
|
||
|
|
47 |
|
|
цилляторы не излучают в направлении отраженного луча и вклад в отраженную волну не дают. Отсюда следует, что в от- раженном луче присутствуют только колебания Е и поэтому он полностью поляризован.
Эффект поляризации отраженного света используется, например, для обнаружения с воздуха пленок нефти на поверх- ности моря.
4.3. Поляризация света при двойном лучепреломлении
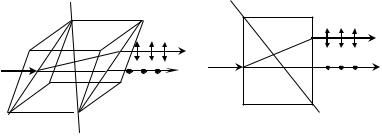
Действие поляризаторов основано на поляризации света при прохождении света в оптически анизотропных средах (это среды, имеющие различные оптические свойства во всех на- правлениях). Все прозрачные кристаллы оптически анизо- тропны. Исключением являются кристаллы, имеющие кубиче- скую кристаллическую решетку (например, каменная соль NaCl). При прохождении света через оптически анизотропные кристаллы наблюдается явление двойного лучепреломления, ко- торое состоит в том, что упавший на кристалл луч разделяется
внутри кристалла на два луча, распространяющихся с различ- ными скоростями и в различных направлениях (рис.4.9). Это яв-
ление впервые было обнаружено датским ученым Э. Бартоли- ном в 1669 г. для исландского шпата.
В зависимости от типа их симметрии оптически анизо- тропные кристаллы бывают одноосные либо двуосные, т.е. име- ют одну или две оптические оси. Оптической осью называется такое направление в оптически анизатропном кристалле, вдоль которого распространяющийся свет не испытывает двойного лучепреломления. Важно отметить, что любая прямая па- раллельная данному направлению, так же является оптической осью кристалла. Примером одноосного кристалла является ис- ландский шпат (рис.4.9 диагональ кристалла ОО' совпадает с оптической осью), а также кварц, турмалин, апатит и другие. К двуосным кристаллам относятся, например, гипс, слюда и топаз.
48
О |
О |
|
|
е |
е |
о |
о |
|
|
О' |
О' |
|
|
а) |
б) |
Рис. 4.9 а − двойное лучепреломление в кристалле. Обыкновенный
инеобыкновенный лучи; б − главное сечение кристалла
Водноосных кристаллах (рис.4.9 а) один из преломлен- ных лучей, образующихся при двойном лучепреломлении, ле- жит в плоскости падения и подчиняется закону Снеллиуса, по-
этому его назвали обыкновенным лучом и обозначают
буквой "о". Скорость обыкновенного луча υо численно одинако-
ва по всем направлениям: υо = c/nо, где nо = const - показатель преломления кристалла для обыкновенного луча. Второй луч называют необыкновенным и обозначают буквой "е", так как он не лежит в плоскости падения и не подчиняется закону прелом-
ления. Соответственно скорость необыкновенного луча υе = c/nе,
где nе - показатель преломления кристалла для необыкновенного луча. Значения nе и υе зависят от направления распространения необыкновенного луча по отношению к оптической оси кри- сталла. Для луча, распространяющегося вдоль оптической оси, nе = nо, υе = υо. Значение nе наиболее сильно отличается от nо для направления, перпендикулярного оптической оси. Все эти раз- личия между обыкновенным и необыкновенным лучами имеют место только внутри кристалла. На выходе из кристалла оба лу- ча распространяются с одинаковой скоростью. В двуосных кри- сталлах оба преломленных луча ведут себя как необыкновен- ные. Исследование обыкновенного и необыкновенного лучей показывает, что на выходе из кристалла оба луча полностью по-
49

ляризованы. Вектор Е обыкновенного луча колеблется перпен- дикулярно главной плоскости (на рисунке 4.9 эти колебания обозначены точками), а вектор Е необыкновенного луча колеб- лется в главной плоскости (на рисунке эти колебания показаны стрелками). Главной плоскостью или главным сечением одноос-
ного кристалла называется плоскость, проходящая через па- дающий луч и оптическую ось кристалла (на рисунке 4.9 б это плоскость чертежа).
Двойное лучепреломление объясняется анизотропией кристаллов. В кристаллах некубической системы ди- электрическая проницаемость ε оказывается зависящей от на- правления. Для одноосных кристаллов диэлектрическая прони- цаемость в направлении оптической оси и диэлектрическая про- ницаемость в направлении, перпендикулярном к ней, имеют различные значения. Поскольку абсолютный показатель пре-
ломления n = εµ , а для большинства кристаллов магнитная
проницаемость µ ≈ 1, то n ≈  ε . Следовательно, из анизотропии диэлектрической проницаемости ε вытекает анизотропия пока- зателя преломления n.
ε . Следовательно, из анизотропии диэлектрической проницаемости ε вытекает анизотропия пока- зателя преломления n.
Допустим, что в точке S внутри одноосного кристалла находится точечный источник света. На рисунке 4.10 показано распространение обыкновенного и необыкновенного лучей в кристалле. Рассмотрим луч, для которого главная плоскость совпадает с плоскостью чертежа, прямая ОО' – оптическая ось.
Волновая поверхность обыкновенного луча является сферой (т.к. nо = const и υо = c/nо = const), необыкновенного луча – эл- липсоидом вращения (т.к. nе≠const и υе = c/nо ≠ const).
На рисунке 4.10 хорошо видно, что наибольшее расхож- дение волновых поверхностей обыкновенного и необыкновен- ного лучей наблюдается в направлении, перпендикулярном оп- тической оси. Сфера и эллипсоид касаются друг друга в точках их пересечения с оптической осью ОО'. Если υе< υо (nе>nо), то эллипсоид вписан в сферу (рис. 4.10 а), такой одноосный кри-
50
