
Волновая оптика и квантовая физика_2010
.pdf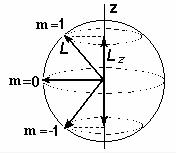
впространстве векторов L и μ, эту
формулу называют формулой про-
странственного квантования. С точ-
ки зрения классического представле- ния об электронной орбите, эта фор- мула определяет возможные дискрет- ные расположения электронных орбит
впространстве по отношению к на- правлению внешнего поля. По отно- шению к другим координатам x и y, положение векторов момента импуль-
са L и магнитного момента μ меняется так, как если бы они вращались во-
круг оси z. Такое вращение называет- ся прецессией (рис. 9.2).
Рис. 9.2. Пространст- венное квантование момента импульса для состояния l = 1 и тра- ектории прецессии.
9.2. Опыт Штерна и Герлаха
Пространственное квантование было продемонстрирова- но в эксперименте с атомными пучками, выполненным О. Штер- ном и В. Герлахом в 1922 г. Для атома водорода пространствен- ное квантование орбитального магнитного момента описывается формулой квантования проекции механического момента. Для более сложных многоэлектронных атомов эта формула несколь- ко видоизменяется, однако и для таких атомов остается в силе основной вывод квантовой теории: проекция магнитного момен- та атома на направление внешнего магнитного поля может иметь только дискретные квантовые значения.
В опыте Штерна и Герлаха пространственное квантова- ние для атомных систем демонстрируется следующим образом. Путем испарения в вакуумной печи серебра или другого металла получают газ, состоящий из возбужденных атомов. С помощью тонких щелей формируется узкий атомный пучок (рис. 9.3), ко- торый пропускается через неоднородное магнитное поле с
111
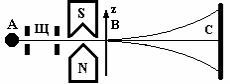
большим градиентом магни- тной индукции ∂B/∂z. Для соз- дания такого магнитного поля используется магнит с ноже- видным полюсным наконеч- ником, вблизи которого на достаточно малом расстоянии пропускается атомный пучок. На атомы, пролетающие в за- зоре магнита, вдоль направ- ления магнитного поля дейст-
вует сила Fz = μz∂B/∂z, обусловленная градиентом индукции не- однородного магнитного поля и зависящая от величины проек- ции магнитного момента атома на направление поля. Эта сила отклоняет движущийся атом в направлении оси z, причем за время пролета между полюсами магнита движущийся атом от- клоняется тем больше, чем больше величина проекции μz.
С позиций классической физики, магнитные моменты атомов вследствие их хаотичного теплового движения, при по- падании в магнитное поле могут иметь любое направление в пространстве. Это должно приводить к возможности различных отклонений атомов. В результате, атомы серебра, быстро проле- тевшие через магнитное поле, должны были образовывать не- прерывную зеркальную полосу в местах оседания на стеклянной пластинке С. Если же, как предсказывает квантовая теория, име- ет место пространственное квантование, и проекция магнитного момента атома принимает только определенные дискретные значения, то под действием силы Fz атомный пучок должен расщепиться на дискретное число пучков, которые, оседая на стеклянной пластинке, дают серию узких дискретных зеркаль- ных полос, куда попадают атомы. Именно этот результат на- блюдался в эксперименте. Таким образом, опыт Штерна и Гер- лаха подтвердил правильность выводов квантовой теории о на-
112
личии пространственного квантования магнитных моментов и моментов импульса атомов.
9.3.Пространственное распределение электрона
ватоме водорода
Графически вероятность нахождения электрона можно изобразить в виде облака, где более темные области соответст- вуют большей вероятности нахождения. «Размеры» и «форму» электронного облака в заданном состоянии атома можно вычис- лить. Для основного состояния атома водорода решение уравне- ния Шредингера дает
|
|
|
|
− |
r |
|
|
ϕ(r ) = |
1 |
|
|
||||
|
|
|
|||||
e r1 |
, |
||||||
3 |
|||||||
|
|
πr |
|
||||
|
|
1 |
|
|
|
|
|
где φ(r) – волновая функция, зависящая только от расстояния r от центра атома, r1 – постоянная, совпадающая с радиусом пер- вой Боровской орбиты. Следовательно, электронное облако в
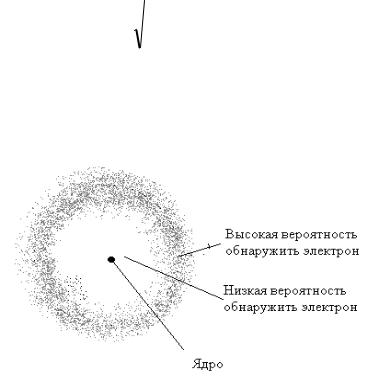
основном состоянии водорода сферически-симметрично, как показано на рис. 9.4.
Рис. 9.4. Электронное облако атома водорода в основном
состоянии n = 1, l = 0.
113
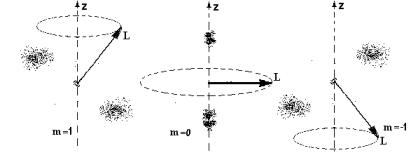
Электронное облако только приблизительно характеризу- ет размеры атома и движение электрона, так как, согласно вы- ражению для волновой функции, вероятность обнаружения электрона не равна нулю для любой точки пространства. На ри- сунке 9.5 изображены электронные облака атома водорода в со- стояниях с n = 2, l =1 и m =1, 0, -1 при наличии магнитного поля.
а) б) в)
Рис. 9.5. Электронные облака атома водорода и прецессия
моментов импульса в состояниях n = 2, l = 1:
а) m = 1; б) m = 0; в) m = -1
Если в этих состояниях определить наиболее вероятные расстояния электрона от ядра, то они будут равны радиусам со- ответствующих Боровских орбит. Таким образом, хотя кванто- вая механика не использует представление о движении электро- на по определенным траекториям, тем не менее, радиусам Бо- ровских орбит и в этой теории можно придать определенный физический смысл.
9.4. Спин электрона
Из квантовой теории следует, что, вследствие симметрии электронного облака, механический и магнитный моменты ато- ма, находящегося в основном, невозбужденном состоянии, рав- ны нулю. Следовательно, если в опыте Штерна-Герлаха обеспе-
114
чить условия, при которых в атомном пучке будут двигаться не- возбужденные атомы, то такой атомный пучок не должен рас- щепляться магнитным полем. Однако эксперимент не подтвер- дил такой вывод квантовой теории. Пучок невозбужденных ато- мов серебра расщепился на два пучка, которые создали две уз- кие зеркальные полоски, сдвинутые симметрично вверх и вниз.
Для объяснения этого и ряда подобных явлений в 1925г. С. Гаудсмит и Дж. Уленбек выдвинули смелую теорию о том, что сам электрон является носителем собственных механическо- го и магнитного моментов, не связанных с движением электрона в пространстве. Эта гипотеза получила название гипотезы о спи- не электрона. Такое название связано с английским словом spin, которое переводится как кружение, верчение. Согласно выдви- нутой теории, электрон обладает собственным моментом им- пульса Ls, который получил название спина, и собственным маг- нитным моментом μs. Спин электрона Ls не квантуется по вели- чине, но квантуется его проекция на направление магнитного
поля Lsz согласно формуле
Lsz = h s, μs = 2μБ s,
спиновое квантовое число s может принимать только два значе- ния s = +1/2 и s = -1/2, то есть у самого электрона во внешнем
поле возможны два направления спина.
Первоначально предполагалось, что спин обусловлен вращением электрона вокруг своей оси. Однако такая модель вращающегося заряженного шарика оказалась несостоятельной, так как расчет показал, что ни при каких допустимых скоростях вращения нельзя индуцировать магнитный момент, равный по величине собственному магнитному моменту электрона. Спин электрона не имеет классического аналога. Он характеризует внутреннее свойство квантовой частицы, связанное с наличием у нее некоторой дополнительной степени свободы движения. Количественная характеристика этой степени свободы − спин −
115
является для электрона такой же величиной как, например, его масса и заряд.
Наличие спина электрона и возможность его пространст- венного квантования во внешнем поле позволило объяснить эф- фекты, которые наблюдались при изучении тонкой структуры оптических спектров ряда атомов. Например, тщательное иссле- дование спектральных линий водорода в магнитном поле пока- зало, что каждая линия состоит из двух близких линий. Это яв- ление получило название тонкой структуры, оно объясняется возможностью двойной ориентации спина.
В1928 г. П. Дирак обобщил квантовую теорию на случай релятивистского движения частиц. Уравнение Дирака значи- тельно сложнее уравнения Шредингера по своей структуре, но из него спиновое квантовое число получается так же естествен- но, как и три квантовых числа при решении уравнения Шредин- гера. Можно упрощенно сказать, что собственные механический
имагнитный моменты у электрона появляются как следствие учета релятивистских эффектов в квантовой теории. Отметим также, что не только электрон, но и многие другие элементар- ные частицы, в том числе и не заряженные, обладают спином.
Таким образом, каждое квантовое состояние электрона в атоме определяется набором четырех квантовых чисел n, l, m, s.
При этом возможны только определенные комбинации этих квантовых чисел:
n = 1, 2, 3, … ∞ ; l = 0, … n -1; m = – l, – l +1, …, l -1, l ; s = ± 1/2.
9.5.Многоэлектронный атом. Правила распределения электронов по орбиталям. Принцип Паули
Вмногоэлектронных атомах вокруг положительно заря- женного ядра движутся несколько электронов, их число равно порядковому номеру атома в таблице Менделеева. У многоэлек- тронных атомов система энергетических уровней усложняется. Это связано с тем, что каждый электрон в данном случае не
116
только притягивается ядром, но и отталкивается другими элек- тронами.
Для многоэлектронного атома стационарное уравнение Шредингера должно содержать потенциальную энергию взаи- модействия ядра со всеми электронами и энергии взаимодейст- вия электронов между собой. Точное аналитическое решение такого уравнения невозможно, на практике пользуются различ- ными приближенными решениями. Например, если считать что взаимодействие электpонов между собой довольно слабое, то в пеpвом пpиближении можно pассматpивать многоэлектронный атом как составленный из нескольких атомов водоpода, вложен- ных дpуг в дpуга, а взаимодействие электpонов учитывать как добавочное. Такая модель удобна, так как для атома водорода известно точное решение и его pезультаты могут быть исполь- зованы.
Решение уравнения Шредингера в таком приближении показывает, что волновые функции для многоэлектронного ато- ма можно выразить через волновые функции атома водорода, при этом энергии возможных состояний электронов зависят уже от двух квантовых чисел n и l. Вследствие этого структура воз- можных состояний (электронных оболочек) оказалась для всех атомов идентичной и сходной со структурой атома водорода. Выяснилось, что все состояния водорода присутствуют и в мно- гоэлектронном атоме независимо от того, заняты они электро- нами или нет. Образно можно сказать, что возможные состояния атома не перестают существовать даже тогда, когда они не за- полнены.
Основное отличие от водорода обнаружилось при запол- нении возможных состояний электронами. Как оказалось, рас- пределение электронов по состояниям для любого невозбужден- ного атома происходит на основании следующих законов:
пpинципа минимума энеpгии и пpинципа запpета Паули. Первый принцип является общим свойством материи, согласно которому
117
любая система стремится к устойчивому состоянию с наимень- шей энергией. Поэтому в невозбужденном атоме электроны стремятся занять состояние с минимальной энергией. Но, как оказалось, в многоэлектронном атоме все электроны не могут находиться в одном и том же состоянии. Внимательный анализ спектров испускания в различных диапазонах частот, а также ис- следование работы выхода электронов из атомов в фотоэффекте привел ученых к выводу, что никакие два электрона в одном и том же атоме не могут находиться в одинаковом квантовом со- стоянии. Иными словами, каждый электрон в атоме имеет свой собственный “адрес”, записанный набором из четырех кванто- вых чисел. Этот закон швейцарский физик В.Паули обосновал теоретически и сформулировал в виде принципа запрета: никакие два электрона в одном атоме не могут характеризоваться оди- наковым набором всех четырех квантовых чисел n, l, m, s.
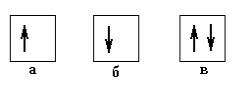
Из принципа Паули вытекает следствие, весьма важное для правил заполнения электронных оболочек: в квантовом со- стоянии, описываемом набором квантовых чисел n, l, m, может находиться максимум два электрона: один − со спиновым кван- товым числом +1/2 и другой − со спиновым квантовым числом –1/2. В химии такое состояние называют орбиталью и схемати-
чески обозначают квадратиком, а находящиеся на орбитали электроны – стрелками (рис. 9.6).
Таким образом, электроны в невозбужденном многоэлек- тронном атоме, последовательно занимают состояния, начиная с
|
|
|
|
|
|
|
имеющего |
минимальную |
||
|
|
|
|
|
|
|
энергию (согласно прин- |
|||
|
|
|
|
|
|
|
ципу |
минимума |
энергии |
|
|
|
|
|
|
|
|
системы), |
при этом, со- |
||
|
а) |
|
б) |
|
в) |
|
||||
|
|
|
|
гласно |
принципу |
запрета |
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Паули, |
в одном и том же |
||
Рис. 9.6. Изображение орбиталей: |
||||||||||
а, б − орбитали, заполненные час- |
квантовом |
состоянии мо- |
||||||||
тично, |
в − полностью заполненная |
|
|
|
|
|||||
|
|
орбиталь. |
|
|
|
|
|
|
||
гут находиться не более двух электронов.
Условно все возможные квантовые состояния распреде- ляют (группируют) по слоям (оболочкам), подслоям (подобо- лочкам) и орбиталям. Как оказалось, свойства атомов определя- ются распределением электронов по этим состояниям.
Квантовым слоем (квантовой оболочкой) называют сово- купность состояний, которым соответствует одно и тем же зна- чение квантового числа n, но разные значения l, m, s. Наиболь- шее число электронов N, которые могут находиться в оболочке равно удвоенному квадрату номера слоя: N = 2n2. Так как энер- гия состояний в многоэлектронном атоме зависит от двух кван- товых чисел n и l, то электроны в квантовом слое могут зани- мать l энергетических уровней. Квантовые слои обозначаются
цифрами, соответствующими номерам слоев. Слои обозначают буквами: К (n = 1), L (n = 2), М (n = 3), N (n = 4) и т.д. Каждый
квантовый слой с номером n условно состоит из n квантовых подслоев (подоболочек), соответствующих состояниям с одними и теми же n и l, но разными m и s. В подслое может находиться
до 2 (2l+1) электронов, подслои обозначаются буквами: s (l = 0), p (l = 1), d (l = 2), f (l = 3), g (l = 4) и т.д. Энергия всех электронов
одного подслоя примерно одинакова.
Каждый подслой в свою очередь, состоит из 2l+1орбиталей, соответствующих состояниям с одними и теми же n, l, m, но разными s. На каждой орбитали может находиться не более двух электронов с разными спиновыми числами
s = ±1/2. Отсюда следует, что в s-подслое может содержаться максимум 2 электрона, в р-подслое – 6, в d – 10, в f – 14, в g – 18
электронов. Соответственно, в слое K может содержаться мак- симум 2 электрона, в слое L – 8, в слое M – 18, в слое N – 32. Структуры и максимально возможные заполнения слоев изо-
бражают в виде формул: K-слой → 1s2 , L-слой → 2s22p6, M-слой → 3s2 3p6 3d10, N-слой → 4s2 4p64d104f14. Используя введенные
понятия, можно условно формулой и графически изобразить
119
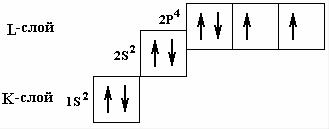
распределение электронов, например атома кислорода О8, сле- дующим образом: символьно- 1s2 2s2 2p4, графически - (рис. 9.7).
Рис. 9.7. Условное графическое изображение орбиталей кислорода.
При заселении орбиталей электроны в первую очередь распола- гаются поодиночке на каждой орбитали, а затем начинается их заполнение вторыми электронами. Эта особенность называется правилом Гунда, она связана с тем, что энергия подслоя при та- ком заполнении несколько меньше. На рис. 9.7 показано приме- нение правила Гунда для кислорода.
9.6. Спектры излучения и поглощения атомов
Если атому сообщить дополнительную энергию, то он может перейти в возбужденное состояние (например, для водо- рода возможны переходы из состояния с n = 1 в состояния с n = 2, 3, 4, … (рис. 9.8). Возбуждение атомов может иницииро- ваться различными способами: за счет столкновений с элемен- тарными частицами – ударное возбуждение, при столкновениях с атомами – тепловое возбуждение и, наконец, при поглощении атомами электромагнитного излучения. Для перехода из основ- ного состояния в возбужденное c главным квантовым числом n атому необходимо передать энергию равную, разности энергий En и E1 состояний. Если энергия передается электромагнитным
120
