Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Саратовский Государственный Аграрный Университет им. Н.И. Вавилова

Предмет:

Математический анализ

Файл:

математический анализ _часть 1

.pdf

Скачиваний:

687

Добавлен:

25.03.2015

Размер:

441.56 Кб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

Саратовский государственный университет им. Н.Г. Чернышевского

Л.Л. Громова, А.М. Захаров, М.А. Осипцев, Л.В. Сахно

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ

Часть 1. Введение в анализ. Числовые ряды. Дифференциальное исчисление

Учебное пособие для студентов механико-математического факультета

ИЗДАТЕЛЬСТВО САРАТОВСКОГО УНИВЕРСИТЕТА

2005

УДК 517(075.8) ББК 22.19.я73

Громова Л.Л., Захаров А.М., Осипцев М.А., Сахно Л.В.

Б82 Практические занятия по математическому анализу: В 3 ч. Часть 1. Введение в анализ. Числовые ряды. Дифференциальное исчисление: Учеб. пособие для студентов мех.-мат. фак. – Саратов: Изд-во Сарат.

ун-та, 2005. – 48 с.: ил. ISBN 5-292-

Пособие является руководством к решению задач по математическому анализу, состоит из трех частей. В первой части рассмотрены теория пределов последовательностей, числовые ряды, предел и непрерывность функций, дифференциальное исчисление функций одного переменного. Приводятся необходимые теоретические сведения, а также многочисленные примеры, в которых разъясняется решение типовых задач. В пособии даются две контрольные работы по изложенным темам.

Для студентов механико-математического факультетов.

Рекомендуют к печати:

Кафедра математического анализа механико-математического факультета Саратовского государственного университета Кандидат физико-математических наук А. Л. Лукашов

	УДК 517(075.8)
	ББК 22.19.я73
	Работа издана в авторской редакции
ISBN 5-292-	© Громова Л.Л., Захаров А.М.,
	Осипцев МА., Сахно Л.В., 2005
	2

ПРОГРАММА КУРСА

1. Теория пределов последовательностей.

Конечные и бесконечные множества, операции над ними. Понятие счетного множества. Понятие действительного числа как бесконечной десятичной дроби. Верхняя и нижняя грани ограниченного множества, их существование.

Понятие последовательности и ее предела. Ограниченность сходящейся последовательности. Сходимость ограниченной монотонной последовательности. Арифметические действия над сходящимися последовательностями. Число и его роль в математическом анализе.

Теоремы о переходе к пределу в неравенствах и о сходимости последовательности, ограниченной двумя сходящимися последовательностями, имеющими одинаковые пределы.

Частичный предел, верхний и нижний пределы, их существование. Теорема Больцано – Вейерштрасса.

2. Числовые ряды.

Понятие числового ряда. Сходимость и сумма ряда. Свойства рядов как свойства последовательностей частных сумм. Абсолютная сходимость ряда, ее связь со сходимостью. Признак мажорации. Геометрический ряд. Признаки Коши и Даламбера абсолютной сходимости ряда. Условная сходимость. Признак Лейбница сходимости ряда.

3. Предел и непрерывность функций.

Понятие предела и непрерывности функции в точке. Эквивалентность определений Коши и Гейне. Арифметические действия над непрерывными функциями. Непрерывность композиции непрерывных функций.

Односторонние пределы и односторонняя непрерывность функции. Существование одностороннего предела монотонной ограниченной функции. Первый и второй замечательные пределы. Теоремы о существовании и непрерывности обратной функции. Классификация точек разрыва функции.

Определение и непрерывность элементарных функций: степенной, показательной, логарифмической, тригонометрических и их обратных. Графики элементарных функций.

4. Дифференциальное исчисление функций одного переменного.

Понятие дифференцируемой функции в точке, производной и дифференциала. Физический и геометрический смысл понятия дифференцируемости и производной функции. Непрерывность дифференцируемой функции. Дифференцируемость и производная сложной и обратной функций. Арифметические действия над дифференцируемыми функциями. Производные элементарных функций.

Локальный экстремум функции, теорема Ферма. Теоремы о среднем значении дифференцируемых функций: Ролля, Лагранжа, Коши. Правило Лопиталя для отыскания предела отношения бесконечно малых или бесконечно больших функций.

Производные высших порядков. Многочлен и формула Тейлора. Достаточное условие экстремума функции. Критерий монотонности функции на интервале. Выпуклые функции, критерий выпуклости. Точки перегиба, необходимое условие точки перегиба.

Методы приближенного вычисления значений функции и решения уравнений.

1. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ

Определение 1. Число х называется пределом последовательности {xn}, если для любого положительного числа ε найдётся номер

n0 такой, что для всех n , начиная с этого номера, выполняется неравенст-

во | xn − x |< ε.

Символически это определение записывается так:

lim x	n	= x ε > 0 n : n ≥ n	0	\| x	n	− x \|< ε.
n→∞	n	0	0		n

Если последовательность имеет предел, то она называется сходящейся. Если предела не существует, то такая последовательность называется расходящейся.

ТЕОРЕМЫ об арифметических операциях над пределами последовательностей

Если существуют пределы lim xn = x и lim yn = y , то

n→∞ n→∞

1) предел суммы последовательностей равен сумме пределов последовательностей:

lim (xn + yn ) = lim xn + lim yn			= x + y ;
n→∞	n→∞	n→∞
2) предел разности последовательностей равен разности пределов
последовательностей:
lim (xn − yn ) =	lim xn −	lim yn	= x − y ;
n→∞	n→∞	n→∞

3) предел произведения последовательностей равен произведению пределов последовательностей:

lim (xn yn ) =	lim xn	lim yn = xy ;
n→∞	n→∞	n→∞

4) предел частного последовательностей равен частному пределов последовательностей:

	xn		lim x	n			x
lim	xn	=	n→∞	n	=		x	( lim yn ≠ 0 ,	yn ≠ 0 ).
lim		=	lim yn		=		y	( lim yn ≠ 0 ,	yn ≠ 0 ).
n→∞ yn			lim yn				y	n→∞
			n→∞
						5

Пример 1. Пользуясь определением предела последовательности,

доказать, что lim 5n +1	= −5 . Если ε = 0,01, то, начиная с какого номера,
n→∞ 1 − n

выполняется неравенство xn −5 < ε.

Решение. Согласно определению предела последовательности, тре-

буется

доказать,

что

ε > 0 n0 : n ≥ n0

выполняется

неравенство

5n +1

+ 5

< ε. Решим это неравенство относительно n.

1 − n

5n +1 + 5 −5n

< ε,

−

< ε,

1 − n

− n

< ε,

6 < ε(n −1) ,

n >

+1.

n −1

Итак, если

n >

+1, то исходное неравенство действительно спра-

ведливо.

Номер

n0 ,

начиная с

которого

выполняется

неравенство

5n +1

< ε, можно найти по формуле

n0 =

+1. Здесь квадратные

1 − n

получаем

скобки

означают

целую

часть

числа.

При

ε = 0,01

n0 =

+1 +1 = 602 .

0,01

Пример 2. Вычислить предел

lim

3n2 +5n − 2

7n2

n→∞ 1 + 2n +

Решение. Разделим числитель и знаменатель дроби

на старшую сте-

пень.

3n2 + 5n − 2

3 +

−

lim

= lim

n→∞ 1 + 2n + 7n2

n→∞

1 2

+ 7

Здесь воспользовались тем, что при n , стремящемся к бесконечно-

сти, 5

→0 ,

2 →0 .

Замечание. Если в числителе и знаменателе записаны многочлены, то предел такой дроби зависит от их степеней.

1.Если степени числителя и знаменателя совпадают, то предел равен отношению коэффициентов при старших степенях.

2.Если степень числителя больше степени знаменателя, то предел равен бесконечности.

3.Если степень знаменателя больше степени числителя, то предел равен нулю.

Пример 3.

Согласно приведенному правилу

2n −3

7n5

− n4 + 72n + 2

lim

= 0 +

;

lim

;

4n + 2

3n +5

+ 2n3 −13

n→∞

n→∞ 3n5

lim

5n5 −83n4 −7n + 2n6

= ∞;

lim

3n4 + n

− n5

= 0 .

100n4 − 2n3

−3

3n4

+12n6

+ 4

n→∞

Пример 4.

Вычислить предел

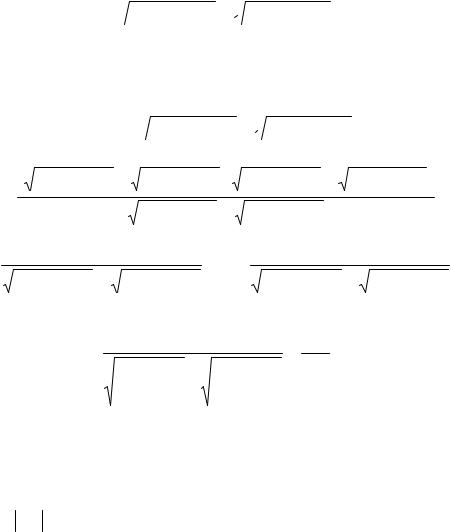
lim ( n2 − 2n − 4 − n2 −6n +5) .

n→∞

Решение. Пределы такого вида широко распространены и решаются домножением на сопряженное выражение с применением формул сокращенного умножения:

lim ( n2 − 2n − 4 − n2 −6n +5) =

n→∞

= lim

(

n2 −2n −4 −

n2 −6n +5)( n2

−2n

−4

+ n2 −6n +5)

n2 −2n −4 + n2 −6n +5

n→∞

= lim

−2n −4 −n2 +6n −5

= lim

4n −9

n2 −2n −4 + n2 −6n +5

n→∞ n2 −2n −4 + n2 −6n +5

n→∞

4 −

= lim

=2.

1+1

n→∞ 1−

−

1−

Определение 2. Последовательность называется бесконечно малой, если ее предел равен нулю.

Определение 3. Последовательность {xn } называется ограниченной, если найдется такое число M , что для всех номеров n выполняется неравенство xn ≤ M .

Известно, что произведение бесконечно малой последовательности на ограниченную является бесконечно малой последовательностью.

Пример 5. Вычислить предел

lim

2 sin 3n

− 2n +

n→∞ n4

Решение. Так как lim

= 0 , а

sin 3n

<1, то

n→∞ n4 − 2n

lim

n2 sin 3n

= 0 .

− 2n +1

n→∞ n4

2. ЧИСЛОВЫЕ РЯДЫ

Для решения задач по теме «Ряды» надо изучить признаки сходимости положительных и знакопеременных рядов, абсолютную и условную сходимость. Краткий перечень сведений из теории приводится ниже в виде теорем.

∞	сходится, то lim an = 0 .
ТЕОРЕМА 1. Если ряд ∑an	сходится, то lim an = 0 .
n=1	n→∞
n=1
Однако для решения задач эта теорема более удобна в следующей
равносильной форме.
ТЕОРЕМА 1'. Если lim an	не равен 0 или не существует, то ряд
n→∞

∞

∑an расходится.

n =1

ТЕОРЕМА 2 (признак сравнения I). Пусть даны два знакоположи-

∞	∞		an
тельных ряда ∑an и	∑bn . Если	lim		= k, 0 < k < ∞, то оба ряды ве-

n =1	n =1	n→∞ bn

дут себя одинаково (одновременно сходятся или расходятся).

ТЕОРЕМА 3 (признак сравнения II). Если члены знакоположитель-

	∞		∞
ных рядов ∑an			(A) и ∑bn	(B) для всех n, начиная с некоторого номера,
	n =1		n =1
удовлетворяют неравенству				an ≤ bn , то из сходимости ряда (B) следует
сходимость ряда (A), а из расходимости ряда (A) следует расходимость ря-
да (B).
ТЕОРЕМА 4 (признак Даламбера). Если для знакоположительного
ряда lim	an+1	= q , то при q >1 ряд расходится, при q <1 ряд сходится.

n→∞	an

При q =1 ряд может сходиться, а может расходиться.

ТЕОРЕМА 5 (признак Коши). Формулировка совпадает с теоремой 4

с той разницей, что q = lim n an .

n→∞

Кроме того полезно помнить поведение некоторых стандартных

рядов.

∞	1
ТЕОРЕМА 6. Ряд ∑		при α >1 сходится, а при α ≤1 расходится.

n =1nα

Отметим, что при α =1 получаем расходящийся ряд ∑∞ 1 , который

n=1 n

называется гармоническим. В школе изучается ряд

∞

1 + q + q2 +…+ qn +…= ∑qn

n =1

– геометрическая прогрессия, который сходится при q <1.

∞

Пусть теперь ряд ∑an (A) имеет члены произвольного знака. Соста-

n =1

∞

вим ряд ∑ an ( A ).

n =1

∞

ТЕОРЕМА 7. Если сходится ряд ∑ an ( A ), то сходится (абсолют-

n =1

∞

но) ряд ∑an (A).

n =1

ТЕОРЕМА 8 (признак Лейбница для знакочередующихся рядов). Ес-

ли модули членов знакочередующегося ряда ∑∞ (−1)n +1 an монотонно убы-

n =1

вают и стремятся к нулю, то этот ряд сходится.

Если ряд ( A ) расходится, а ряд (A) сходится, то он называется схо-

дящимся условно.

При решении примеров полезно знать некоторые пределы. Напомним их.

ln(1 +

)

1 )n = e,

a n −1

lim n n =1,

lim (n +

lim

=1,

lim

= ln a, a > 0 .

n→∞

Пример 6. Установить сходимость или расходимость ряда

∑∞ n2 .

n=1n(n +1)

Решение. Полезно сразу использовать теорему 1'. Здесь an =

n(n

+1)

и lim

=1 ≠ 0 , значит, данный ряд расходится.

n→∞ n(n +1)

∞

Пример 7. Установить сходимость или расходимость ряда ∑

n =14n

Решение.

> 0 , поэтому можно применять теоремы 1 – 5.

4n +1

(n +1)2

Из них проще всего взять признак Даламбера. Запишем an+1 =

. То-

4n+1 +1

an+1

(n +1)2 (4n +1)

4n +1

гда lim

= lim

1 <1. Ряд сходится.

(4n+1 +1)n2

n→∞

n→∞ 4n+1 +1

Пример 8. Установить сходимость или расходимость ряда

∞

2n +

∑(

) 2 .

3n +

n =1

2n +1

)

Решение.

an = (

> 0 . Применимы теоремы 1 – 5. Здесь удоб-

3n +1

нее

взять

признак

Коши

легко

вычислить

2n +1)

lim n an

= lim (

<1 , следовательно, ряд сходится.

n→∞

3n +1

Чтобы воспользоваться теоремой 2, надо сначала выбрать для данно-

∞

го ряда

∑an другой ряд

∑bn так, чтобы lim

≠ 0

(или ∞) и поведение

n =1

n→∞ bn

∞

ряда ∑bn было уже известно.

n =1

Пример 9. Установить сходимость или расходимость ряда

∞

∑

2n + 3

n =1

Решение.

an =

> 0 . Так как

lim

= lim

= 0 , то данный

2n +3

2n + 3

n→∞

ряд может как сходиться, так и расходиться. Теоремы 4, 5 ответа не дают, q =1. Так как знаменатель линейно зависит от n, то берём для сравнения

∞

ряд ∑

. Тогда

lim

. Оба ряда ведут себя одинаково.

2n +

n =1n

n→∞ bn

n→∞

∞

расходится (гармонический), то данный ряд тоже расхо-

Так как ряд ∑

n =1

дится.

Замечание. Если бы

, то b

. В случае дробного по-

2nk

казателя решение аналогично.

Пример 10. Установить сходимость или расходимость ряда

∞

∑

n =1 n3 − n +1

Решение.

Находим,

что

n3 −n +1 = n 32 1 − 1

+ 1 , поэтому для

сравнения берём ряд с общим членом b

( α =3/ 2 >1, ряд сходится).

1 / 51 2 3 4 5 > Следующая >>>