4.2 Интервальная оценка показателей надежности.

В лабораторной работе №3 были получены оценки числовых характеристик выборочной совокупности наблюдений – среднее значение ресурса и его среднеквадратическое отклонение. Можно ли утверждать, что, где– это математическое ожидание ресурса, являющееся его истинным средним значением? Нет, т.к. оценка среднего значенияопределена по выборке из генеральной совокупности. Поскольку выборка случайна, то и оценка среднего значенияв известной мере также носит случайный характер (рисунок 3). Следовательно, при использовании величины вместомы будем совершать некоторую ошибку. Необходимо определить величину этой ошибки при заданной степени уверенности в том, что она не выйдет за известные пределы.При решении этой задачи используют доверительный интервал, характеризующий точность оценки, и доверительную вероятность, соответствующую, как правило, заданной достоверности.

Таким образом, формулировка задачи интервального оценивания показателей надежности следующая: требуется оценить, в интервал какой длины с заданной доверительной вероятностьюпопадет неизвестное значение, если известна его оценка. Границы интервала обозначаются:– нижняя граница;– верхняя граница. Значенияиопределяются по вероятности.

Рис.3. Генеральная и выборочная совокупности наблюдений

Решение задачи:

Из теории вероятностей известно, что вероятность попадания любой СВс плотностью распределенияв заданный интервал (в данном случае;) вычисляется по формуле:

(4.5)

Зависимость (4.5) позволяет решать и обратную задачу: задаваясь доверительной вероятностью(при исследовании надежности с.-х. техники) по известному закону распределения найти границы, а следовательно, и длину интервала, т.е. определить точность оценки при заданной доверительной вероятности. Очевидно, чем меньше этот интервал при одном и том же значении, тем оценка точнее. Заметим, что зависимость (4.5) содержит две неизвестных величины – нижнюю и верхнюю границы доверительного интервала. В этой связи преобразуем ее к виду

(4.6)

О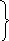тсюда,

. (4.7)

Геометрическая интерпретация зависимостей (4.7) представлена на рис.4.

Рис. 4. Геометрическая интерпретация границ доверительного интервала

Из зависимостей (4.6), (4.7) и рисунка 4 очевидно, что вероятность должна быть большой (это желательный исход), а– маленькой (нежелательный исход). Обычно задаются симметричными их значениями:

.

Таким образом, зная закон распределения СВ и задавшись значением , решают уравнения (4.7) относительноии определяют границы и длину доверительного интервала:

.

Другими словами, определяют точность оценки показателей надежности с требуемой (заданной) доверительной вероятностью. Конкретный вид зависимостей (4.7) определяется видом ТЗР случайной величины.

Нормальный закон распределения. В условиях решаемой задачи случайной величиной является оценка среднего значения ресурса с плотностью распределения

,

где – среднеквадратическое отклонение оценки среднего значения ресурса;– среднеквадратическое отклонение ресурса, вычисленное по генеральной совокупности,истинное значение среднего ресурса – МОЖ ресурса.

Так как в данной задаче неизвестно, а вместо него используется оценка, вычисленная в лр №3, то доверительные границы определяют по формуле

, (4.8)

где – коэффициент Стьюдента (приложение 4), увеличивающий на некоторую величину длину доверительного интервала (;)с учетом приближенной оценки .

Результат, полученный по зависимости (4.8), трактуется следующим образом: с вероятностью можно утверждать, что истинное неизвестное нам значение среднего ресурса находится в пределах

,

где соответственно нижняя и верхняя доверительные границы среднего ресурса.