3.3 Физические (параметрические) методы расчета надежности.

Применяют для расчета БО, Д и Схр О, для которых известны их механизмы деградации под влиянием внешних и внутренних факторов.

Методы основаны на описании процессов деградации математическими моделями непревышения илинакопления повреждений, позволяющими вычислить ПН по свойствам материалов, используемых в объекте с учетом его конструкции, планируемой технологии изготовления и условий эксплуатации.

Здесь имеется ввиду непревышение нагрузок над «несущей способностью». Поскольку и те и другие в общем случае являются случайными величинами, то решение задач в рамках этих моделей базируются на вероятностных подходах.

По схеме моделей непревышения или мгновенного разрушениясостояние конструкции изменяется не монотонно, то приближаясь, то удаляясь и опять приближаясь к Пр и так до тех пор, пока не достигнет его. Прс в рамках этой схемы наступает при условииS>R,

Здесь S-нагрузка;

R-несущая способность конструкции

Очевидно, что область безотказной работы определяется условием не превышения S<R.

Пусть SиRслучайные величины имеющие нормальное распределение с параметрами

m_s, _s

m_R,_R

В качестве параметра состояния конструкции (элемента) примем разность

Х=R-S

Найдем вероятность не разрушения элемента, то есть P(x>0)

Т. к. случайный параметр Х является композицией нормального распределения СВ SиR, то он также подчиняется НЗР с параметрами

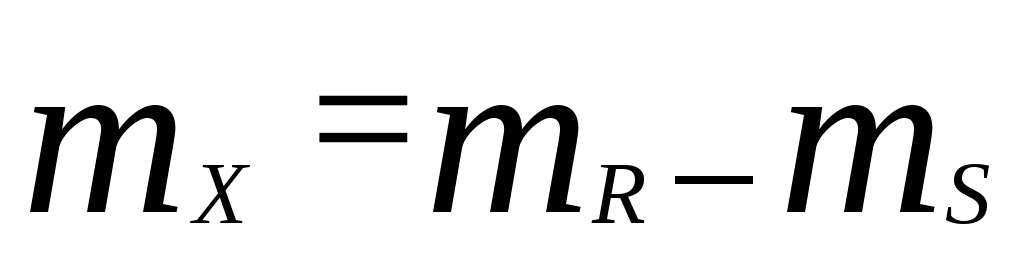
где коэффициент корреляции СВRиS.

Плотность нормального распределения параметра Х имеет вид

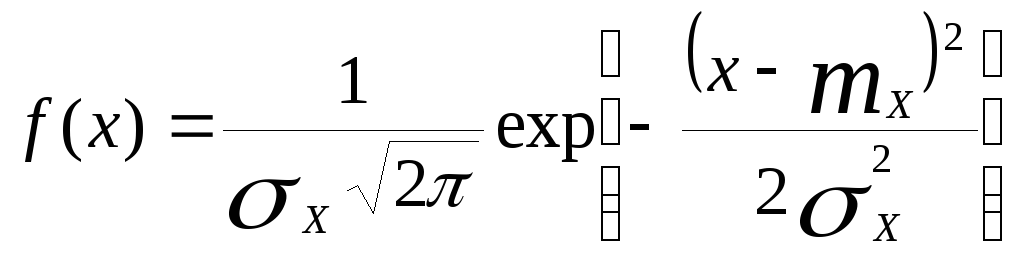
Т.к. X=R=S, то очевидно что элемент будет работать безотказно при Х>0.Вероятность этого события равна площади под кривойf(х) при Х>0

x

0

Аналитически она вычисляется по зависимости

, (1)

при

Введем переменную , тогда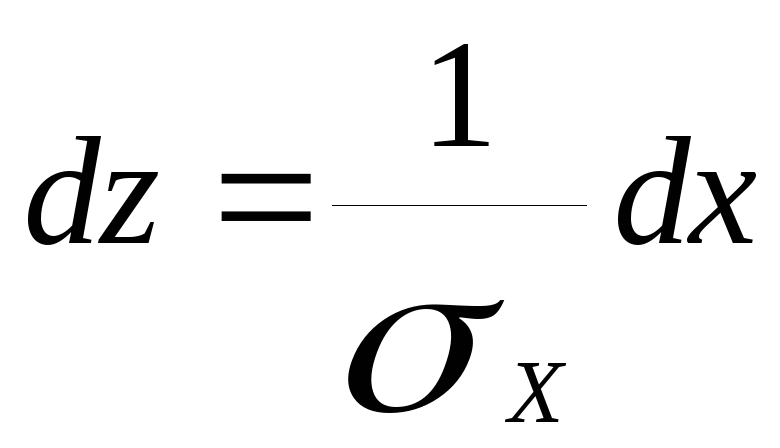

Определим пределы изменения новой переменной z

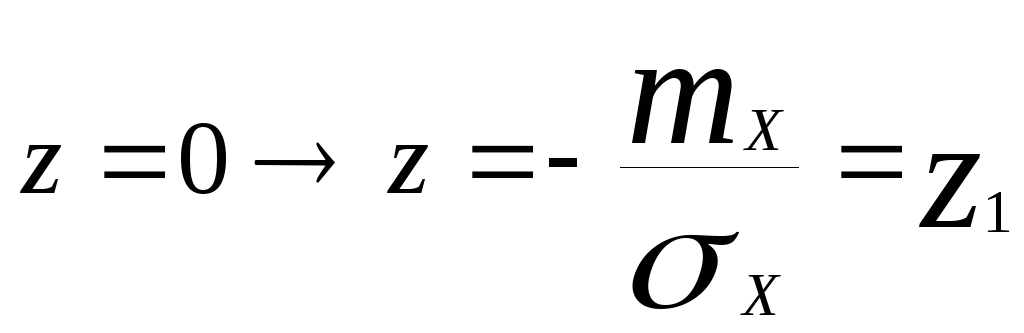, при

Подставив полученное в (1) будем иметь

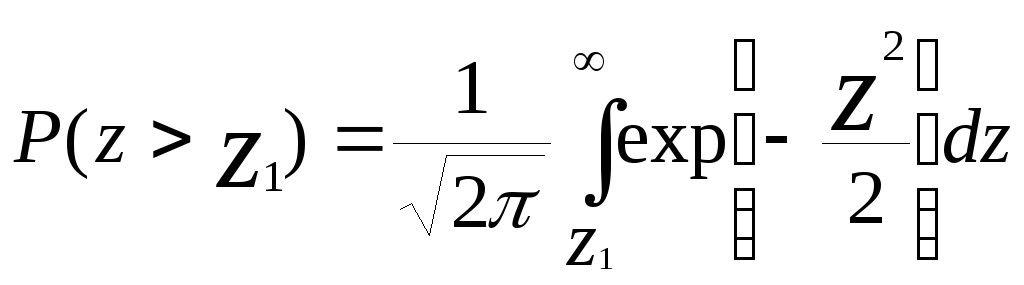
Геометрическая трактовка последнего

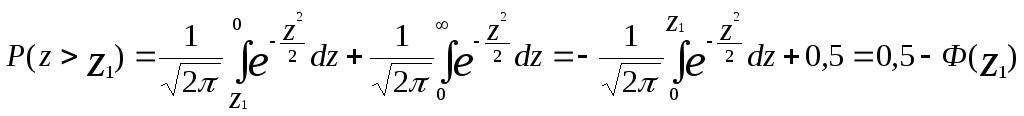
где

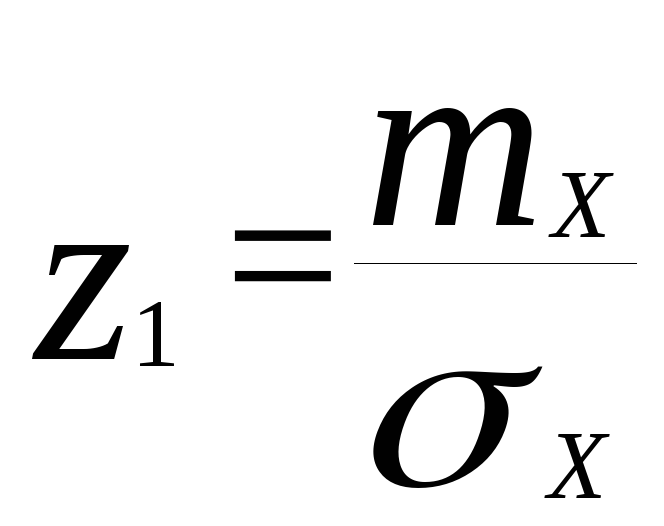
Т.е.

Следует учесть, что

На практике удобнее оперировать не абсолютными величинами и,и, а величинами относительными:

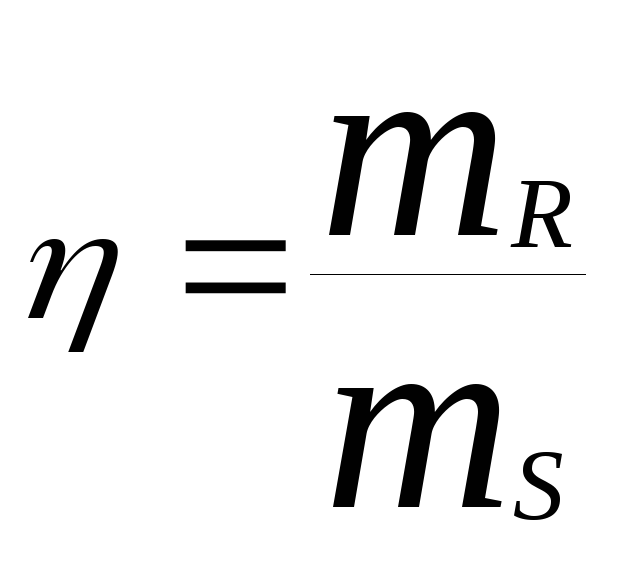-- средне статистический коэффициент запаса несущей способности.

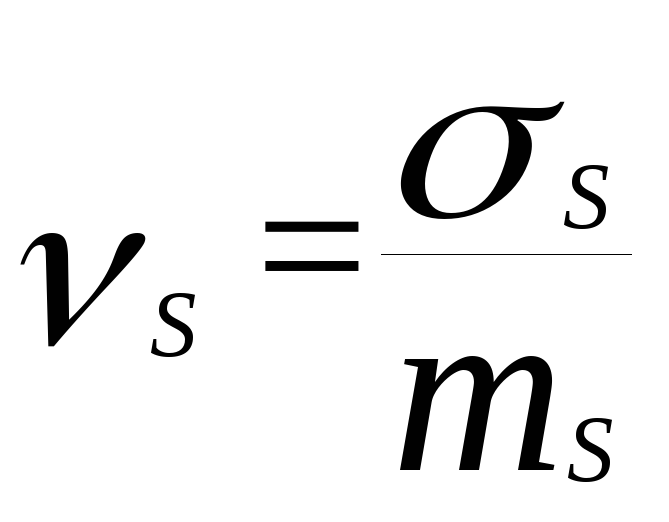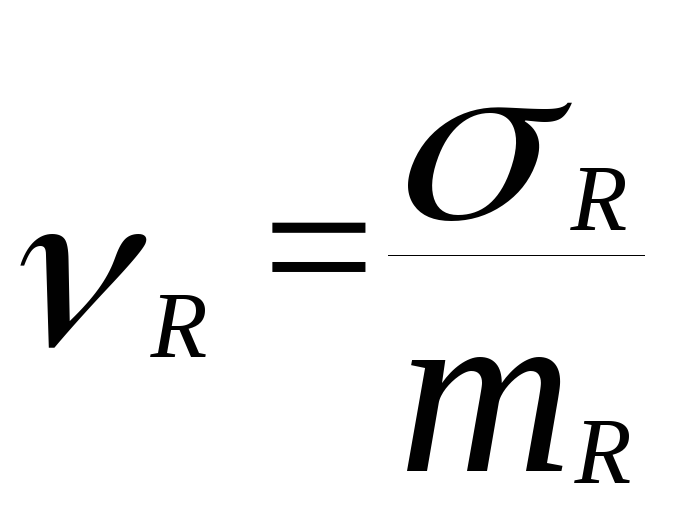-и- коэффициенты вариации нагрузки и несущей способности.

В этих условиях будет определяться зависимостью

,

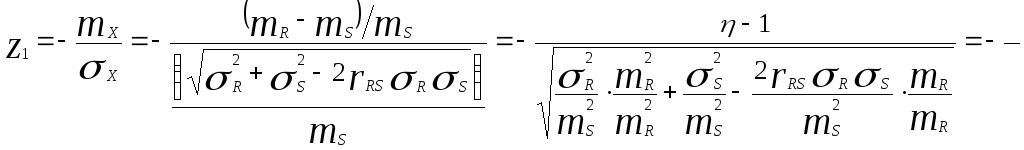
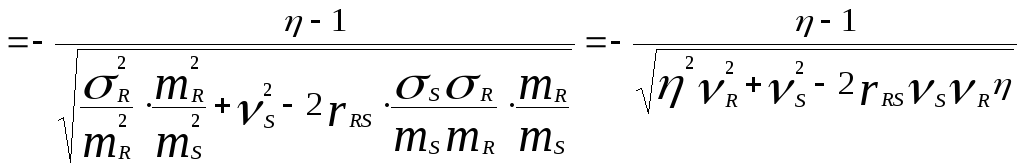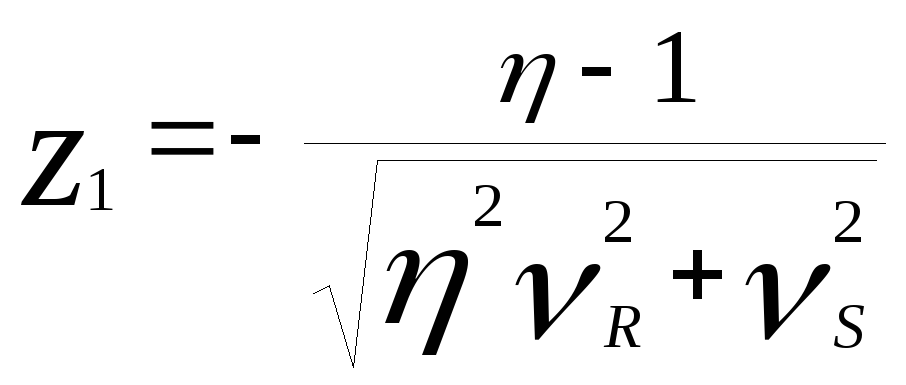Т.к. в большинстве случаев SиRстатистически независимы , то. Тогда, (2)

Т.е. ВБР элемента ,

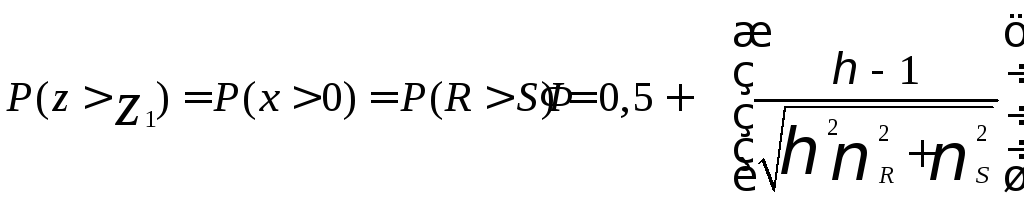Используя (2) можно решить и обратную задачу – задавшись требуемой ВБР. определитьа из (2) определить запас прочности, обеспечивающий требуемую ВБР.

Последняя зависимость позволяет вычислить коэффициент запаса несущей способности т.е. характеристику нагруженного резерва при заданной ВБР конструкции .

,откуда .Т.к., то и

.

В этих условиях коэффициент запаса несущей способности вычисляется по зависимости

,

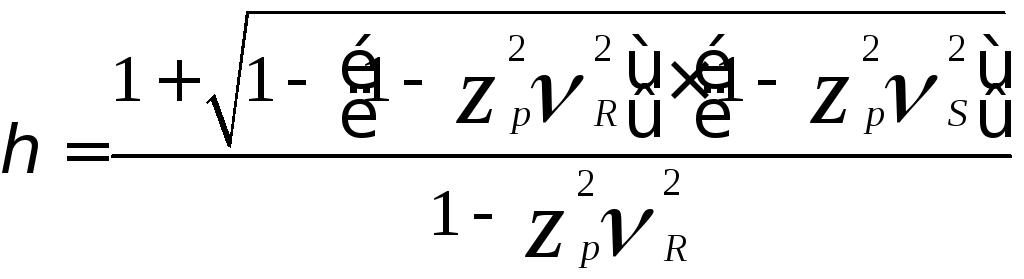Этот результат получен для 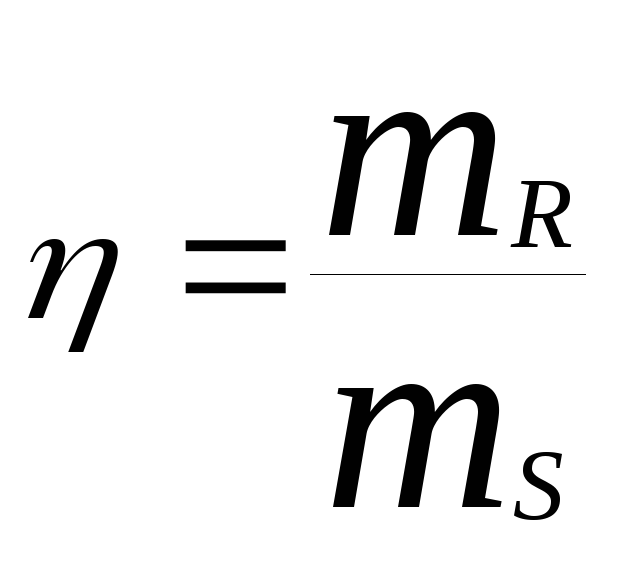,для случая когдаине зависят от времени.

Подход Проникова

В н/вр используются 2 класса моделей непревышения:

-многопараметрические

-однопараметрические

S₃

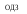
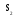
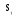
Рис.1

Многопараметрическая модель может быть представлена моделью выбросов некоторого случайного процесса за границы допустимой области.

Например:

-состояние объекта характеризуется параметрами S₁, S₂, S₃;

-известны их допустимые значения;

-границы детерминированы.

Геометрическая трактовка модели выглядит следующим образом (см. рис.1).

В этом случае ПН- ВБР объекта будет иметь

P(t)=P(S)

Следует иметь в виду, что параметров, определяющих ТС объекта много, они, как правило, имеют различную физическую природу, характеризуются различными распределениями, поэтому модели очень сложны и допускают прямые аналитические решения лишь в редких случаях.

Основным методом их решения является статистическое моделирование.

Профессором Прониковым предложены модели, разрешаемые последовательно для ряда независимых параметров S_к, к=1,...,К с последующим обобщением полученных результатов.

Сущность определения значений ПН в рамках данной модели в следующем.

1. На основе анализа функциональной схемы объекта выбирается статистически независимые выходные параметры ,k=1, .

2. Определяется вероятность безотказной работы О по каждому из параметров,k=1, .

Например, в условиях нормального распределения значения параметра

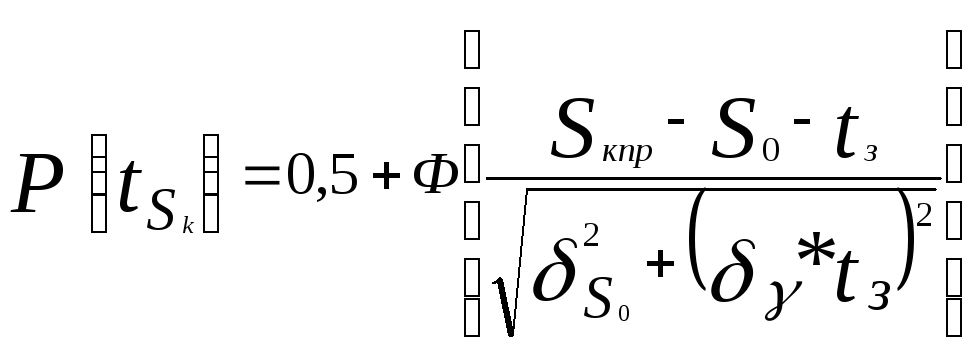
где: Ф – функция Лапласа, значение которой табулировано;

- предельное значение выходного параметра;

,- МОЖ и СКО выходные параметры приt = 0;

- скорость деградации параметра;

- заданный временной интервал;

- СКО скорости деградации параметра.

3. Определяется ВБР объекта по всем выходным параметрам.

.

Хотя решение однопараметрических моделей проще многопараметрических, тем не менее и здесь возникает достаточно много трудностей, основными из которых являются получение на стадии проектирования достоверных оценок таких величин, как и.