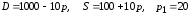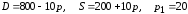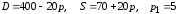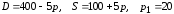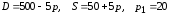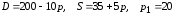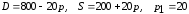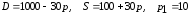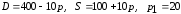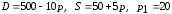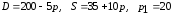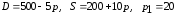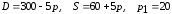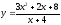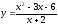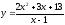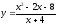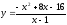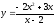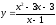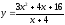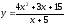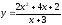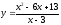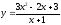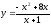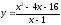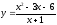мат.анализ контрольная работа
.docx
Функция. Функции в экономике.
Задание 1
Общее условие для всех вариантов.
Заданы функции
спроса
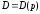 и предложения
и предложения
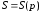 на товар в зависимости от цены
на товар в зависимости от цены
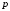 .
Требуется:
.
Требуется:
-
найти область определения и множество значений функций;
-
найти объем предложения и объем спроса товара по цене
 ;
определить, что будет - избыточное
предложение или избыточный спрос;
вычислить выручку продавцов
;
определить, что будет - избыточное
предложение или избыточный спрос;
вычислить выручку продавцов
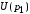 ;
;
-
найти равновесную цену
 ,
равновесный объем продаж
,
равновесный объем продаж
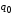 и выручку продавцов
и выручку продавцов
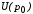 ;
;
-
построить графики функций
 и
и
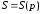 в одной системе координат, указать
значение
в одной системе координат, указать
значение
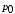 .
.
|
№ варианта |
Числовые данные |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
Самостоятельно: Свойства функций: четные и нечетные функции, их свойства. Основные элементарные функции.
Задание 1*(дополнительное)
Найти область определения функции, исследовать заданную функцию на чётность.
-
f(x)=
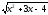 ; b)
f(x)=
; b)
f(x)=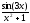 ;
; -
a) f(x)=arcsin(2x-3); b) f(x)=
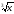 cos(x);
cos(x); -
a) f(x)=lg(3x-x
 );
b) f(x)=tg(2x)+
);
b) f(x)=tg(2x)+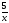 ;
; -
a) f(x)=
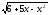 ;
b) f(x)=
;
b) f(x)=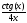 ;
; -
a) f(x)=arcos(5+3x); b) f(x)=
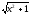 -
- ;
; -
a) f(x)=lg(
 );
b) f(x)=(x
);
b) f(x)=(x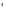 -1)
sin(x);
-1)
sin(x); -
a) f(x)=
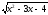 ;
b) f(x)=
;
b) f(x)=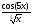 ;
; -
a) f(x)=arcsin(
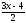 );
b) f(x)=(x
);
b) f(x)=(x -3x)
tg(x);
-3x)
tg(x); -
a) f(x)=(x
 -3x)
tg(x); b) f(x)=ctg(x
-3x)
tg(x); b) f(x)=ctg(x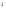 +
+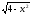 ;
;
-
a) f(x)=
 ;
b) f(x)=
;
b) f(x)=
 +
+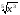 ;
; -
a) f(x)= arccos(
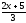 );
b) f(x)=
);
b) f(x)=
 ;
; -
a) f(x)= ln(4x+x
 );
b) f(x)=
);
b) f(x)=
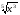 cos(3x);
cos(3x); -
a) f(x)=
 ;
b) f(x)=
;
b) f(x)=
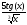 ;
; -
a) f(x)= arctg(
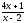 );
b) f(x)=
);
b) f(x)=
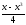 -ctg(2x);
-ctg(2x); -
a) f(x)=
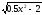 ;
b) f(x)=
;
b) f(x)=
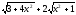 ;
;
-
a) f(x)= arcctg(
 );
b) f(x)=
);
b) f(x)=
 ;
; -
a) f(x)= lg(5x+x
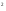 );
b) f(x)=
);
b) f(x)=
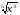 cos(5x);
cos(5x); -
a) f(x)= ln(
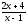 );
b) f(x)= tg(3x)+
);
b) f(x)= tg(3x)+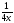 ;
; -
a) f(x)=
 ;
b) f(x)=
;
b) f(x)=
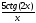 ;
; -
a) f(x)= arcsin(
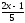 );
b) f(x)=
);
b) f(x)=
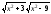 .
.
Предел и непрерывность.
Задание 2
Вычислить пределы функций, не пользуясь правилом Лопиталя.
-
а)
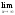
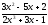 ;
б)
;
б)
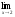
 ;
;
-
а)
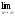
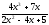 ;
б)
;
б)
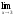
 ;
; -
а)

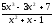 ;
б)
;
б)
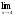
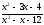 ;
; -
a)
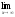
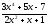 ;
б)
;
б)

 ;
; -
a)
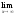
 ; b)
; b)
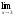
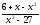 ;
; -
a )
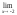
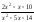 ;
b )
;
b )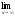
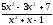 ;
;
-
a )
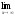
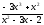 ; b )
; b )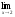
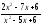 ;
; -
a )
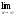
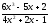 ; b)
; b)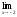
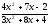 ;
; -
a )

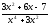 ; b )
; b )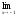
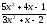
-
a )

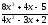 ; b )
; b )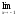

-
a )


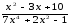 ; b )
; b )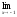
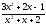
-
a )
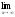
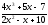 ; b )
; b )
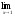
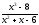 ;
;
-
а)
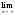
 ;
б)
;
б)

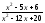 ;
; -
а)
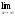
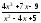 ;
б)
;
б)
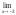
 ;
; -
а)
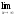
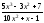 ;
б)
;
б)
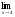
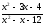 ;
; -
a)
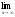
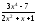 ;
б)
;
б)

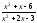 ;
; -
a )

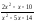 ;
b )
;
b )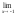
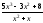 ;
;
-
a )
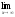
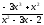 ; b )
; b )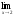
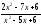 ;
; -
a )
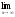
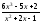 ; b)
; b)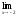
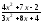 ;
; -
a )
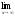
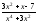 ; b )
; b )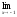
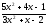 ;
;
Задание 3
Задана функция y=f(x) и два значения аргумента x1 и x2 . Требуется: 1) найти область непрерывности функции и установить, является ли данная функция непрерывной для каждого из заданных значений аргумента; 2) в случае разрыва функции сделать вывод о характере точки разрыва; 3) сделать схематический чертёж.
f(x)=2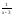 +1
, x
+1
, x =
4, x
=
4, x =3
;
=3
;
f(x)= , x
, x =
0 , x
=
0 , x =
1 ;
=
1 ;
f(x)=4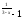 , x
, x =
3 , x
=
3 , x =
4 ;
=
4 ;
f(x)=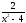 , x
, x =
2 , x
=
2 , x =
3
=
3
f(x)=
12 , x
, x =
1 , x
=
1 , x =
0 ;
=
0 ;
f(x)=
 , x
, x =
0 , x
=
0 , x =
2 ;
=
2 ;
f(x)= 2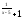 , x
, x =
5 , x
=
5 , x =
6 ;
=
6 ;
f(x)=
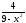 , x
, x =
2 , x
=
2 , x =
3 ;
=
3 ;
f(x)= 3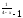 , x
, x =
4 , x
=
4 , x =
6 ;
=
6 ;
f(x)= 4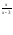 , x
, x =
3 , x
=
3 , x =
4 ;
=
4 ;
f(x)= 8 , x
, x =
7 , x
=
7 , x =
5 ;
=
5 ;
f(x)= 9 , x
, x =
-1 , x
=
-1 , x =
0 ;
=
0 ;
f(x)= 2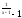 , x
, x =
1 , x
=
1 , x =
0 ;
=
0 ;
f(x)=
 , x
, x =
-5 , x
=
-5 , x =
4 ;
=
4 ;
f(x)= 3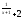 , x
, x =
-1 , x
=
-1 , x =
0 ;
=
0 ;
f(x)=
 , x
, x =
3 , x
=
3 , x =
5 ;
=
5 ;
f(x)= 4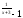 , x
, x =
-3 , x
=
-3 , x =
-2 ;
=
-2 ;
f(x)= 8 , x
, x =
0 , x
=
0 , x =
1 ;
=
1 ;
f(x)=
3 , x
, x =
-2 , x
=
-2 , x =
-4 ;
=
-4 ;
f(x)=
7 , x
, x =
-2 , x
=
-2 , x =
0 ;
=
0 ;
Самостоятельно: Первый и второй замечательные пределы. Эквивалентные бесконечномалые.
Задание 2*(дополнительное)
Вычислить пределы функций, не пользуясь правилом Лопиталя (использовать эквивалентность бесконечно малых и 2-ой замечательный предел).
-
а)

 ; б)
; б)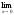
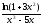 ; в)
; в)
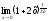 ;
; -
а )
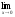
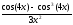 ; б )
; б )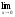
 ; в)
; в)
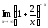 ;
; -
а )
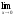
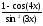 ; б )
; б )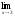
 ; в)
; в)
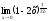 ;
; -
а )
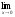
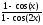 ; б )
; б )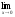
 ; в)
; в)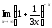
-
а )

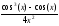 ; б )
; б )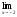
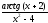 ; в)
; в)
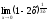 ;
; -
а )
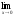
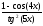 ; б )
; б )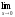
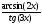 ; в)
; в)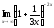
-
а )
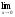
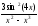 ; б )
; б )
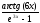 ; в)
; в)
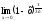 ;
; -
а )
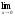
 ; б )
; б )
 ; в)
; в)
-
а)
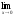
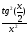 ; б )
; б )
 в)
в)
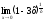 ;
; -
а)

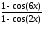 ; б)
; б)
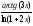 ; в)
; в)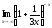 ;
; -
а)
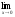
 ; б)
; б)
 ; в)
; в)
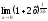 ;
; -
а )
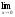
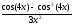 ; б )
; б )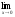
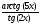 ; в)
; в)
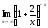 ;
; -
а )

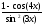 ; б )
; б )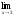
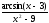 ; в)
; в)
 ;
; -
а )
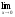
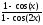 ; б )
; б )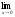
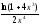 ; в)
; в)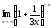
-
а )
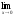
 ; б )
; б )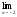
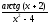 ; в)
; в)
 ;
; -
а )
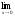
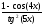 ; б )
; б )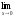
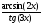 ; в)
; в)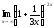
-
а )

 ; б )
; б )
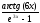 ; в)
; в)
 ;
; -
а )

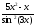 ; б )
; б )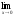
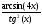 ; в)
; в)
-
а)

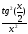 ; б )
; б )
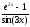 в)
в)
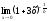 ;
; -
а)
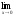
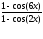 ; б)
; б)
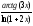 ; в)
; в)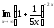 .
.
Задание 3*(дополнительное)
Найти точки разрыва функции и определить характер разрыва. Сделать чертёж.
-
f(x)=
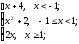
-
f(x)=
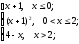
-
f(x)=
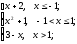
-
f(x)=

-
f(x)=

-
f(x)=
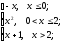
-
f(x)=
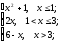
-
f(x)=
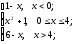
-
f(x)=
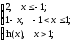
-
f(x)=

-
f(x)=
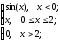
-
f(x)=

-
f(x)=

-
f(x)=
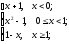
-
f(x)=
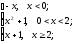
-
f(x)=

-
f(x)=

-
f(x)=
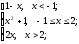
-
f(x)=

-
f(x)=

Задание 4
Исследовать методами дифференциального исчисления функцию. Построить график этой функции, используя результаты исследования.
Самостоятельно: Производная сложной функции. Наибольшие и наименьшее значения функции на отрезке. Производные в экономике.
Задание 4*(дополнительное)
Найти наименьшее и наибольшее значения функции у = f(х) на заданном отрезке [а, в].
-
у = ln (х2 –2х+2), [0, 3];
-
y = x3 –12x+17, [-1, 3]
-
y = x/2 +cosx, [П/2, П];
-
y = (x+2) e1-x, [-2, 2]
-
y = ln (x2 +2x+4), [-3, 0];
-
y = x4 +4/3x3 –7, [-2, 0]
-
y = x3 –27x-17, [-3, 4];
-
y = √3/2x-sinx, [0, П/2]
-
y = (x-2) ex , [-2, 2];
-
y = e4x - x2 , [1, 3]
-
y = 3x4 –16x3 +2, [-3, 1];
-
y = 81x – x4 , [-1, 4]
-
y = ln (x2 –4x+5), [0, 3];
-
y = x3 –9/2x2 –12x, [-2, 0]
-
y = x3 +9/2x2 –12x, [-5, -3];
-
y = x/2+sinx, [0, П]
-
y = e6x - x2 , [-3, 4];
-
y = √3/2x+cosx, [0, П/2]
-
y = x3 +3/2x2 –18x, [-4, -2];
-
y = e2x - x2 , [-1, 2]
Задание 5* (дополнительное)
Задача на экономические приложения производных функций одной переменной.
-
Поступления от реализации производственной продукции
 выражаются функцией
выражаются функцией
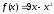 ,
а затраты, связанные с производством
продукции в количестве
,
а затраты, связанные с производством
продукции в количестве
 ,
записываются функцией
,
записываются функцией
 .
Определите оптимальный объем производства,
обеспечивающий максимум прибыли.
.
Определите оптимальный объем производства,
обеспечивающий максимум прибыли.
-
Найти эластичность
 функции спроса
функции спроса
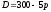 по цене и эластичность
по цене и эластичность
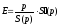 функции предложения
функции предложения
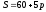 по цене при
по цене при
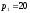 .
Определить, на сколько процентов
изменятся спрос и предложение, если
цена увеличится на 5%..
.
Определить, на сколько процентов
изменятся спрос и предложение, если
цена увеличится на 5%..
-
Затраты, связанные с производством продукции, определяются функцией
 .
Определите объем производства,
обеспечивающий минимальные затраты.
Дайте экономическое истолкование
результату.
.
Определите объем производства,
обеспечивающий минимальные затраты.
Дайте экономическое истолкование
результату.
-
Объем
 выпущенной продукции и выручка
выпущенной продукции и выручка
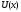 ,
полученная от реализации, заданы
функцией
,
полученная от реализации, заданы
функцией
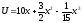 .
Найдите, при каком объеме продукции
выручка минимальна. Вычислите предельную
выручку.
.
Найдите, при каком объеме продукции
выручка минимальна. Вычислите предельную
выручку.
-
Цена на товар составляет 250 руб., издержки производства этого товара равны
 ,
где
,
где
 - число единиц произведенного товара.
Найти, при каком количестве товара
функция прибыли принимает максимальное
значение.
- число единиц произведенного товара.
Найти, при каком количестве товара
функция прибыли принимает максимальное
значение. -
Издержки производства продукции определяются функцией
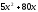 ,
где
,
где
 - число единиц произведенной за месяц
продукции. Продукция продается по цене
280 руб. за изделие. Сколько изделий нужно
произвести и продать, чтобы прибыль
была максимальна?
- число единиц произведенной за месяц
продукции. Продукция продается по цене
280 руб. за изделие. Сколько изделий нужно
произвести и продать, чтобы прибыль
была максимальна?
-
Количество произведенной за день продукции
 зависит от числа рабочих в сборочном
цехе следующим образом:
зависит от числа рабочих в сборочном
цехе следующим образом:
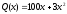 ,
где
,
где
 - число рабочих. Вычислить значение
прироста выработки за
неделю,
вызванное добавлением одного рабочего.
- число рабочих. Вычислить значение
прироста выработки за
неделю,
вызванное добавлением одного рабочего.
-
Вычислить предельную выручку, если известны уравнение спроса
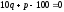 и значение цены
и значение цены
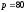 на продукцию (
на продукцию (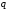 - количество продукции,
- количество продукции,
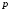 - цена продукции). Что она показывает?
- цена продукции). Что она показывает? -
Производитель реализует продукцию по цене
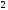 ден. ед. за единицу, а общие издержки
равны
ден. ед. за единицу, а общие издержки
равны
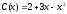 ден. ед., где
ден. ед., где
 - количество продукции. Известно, что
наибольшая прибыль достигается при
выпуске 0,5 ед. продукции. Чему равны
полный доход
- количество продукции. Известно, что
наибольшая прибыль достигается при
выпуске 0,5 ед. продукции. Чему равны
полный доход
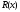 и общие издержки
и общие издержки
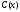 при оптимальном плане выпуска продукции?
при оптимальном плане выпуска продукции?
-
Вычислить предельную выручку, если известно уравнение спроса
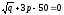 и значение цены
и значение цены
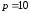 на некоторую продукцию (
на некоторую продукцию (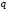 - количество продукции,
- количество продукции,
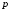 - цена продукции).
- цена продукции).
-
Вычислить эластичность функции спроса
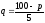 в точке
в точке
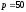 (
( - количество продукции,
- количество продукции,
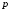 - цена продукции). Дать экономическое
истолкование результату. Вычислить
процентное изменение спроса, если цена
уменьшилась на 2%.
- цена продукции). Дать экономическое
истолкование результату. Вычислить
процентное изменение спроса, если цена
уменьшилась на 2%.
-
Задана зависимость
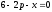 ,
связывающая количество продукции
,
связывающая количество продукции
 и цену
и цену
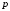 товара. Постоянные издержки производства
составляют
товара. Постоянные издержки производства
составляют
 ден. ед., а переменные затраты на одну
единицу продукции равны
ден. ед., а переменные затраты на одну
единицу продукции равны
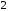 ден. ед. Запишите функции дохода
ден. ед. Запишите функции дохода
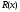 ,
общих издержек
,
общих издержек
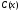 и прибыли
и прибыли
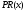 .
Постройте графики функций
.
Постройте графики функций
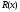 ,
,
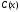 ,
,
 .
.
-
Зависимость спроса от цены выражается формулой
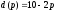 .
Запишите функцию выручки от цены. При
каких значениях цены выручка возрастает?
Вычислите эластичность спроса на товар
по цене
.
Запишите функцию выручки от цены. При
каких значениях цены выручка возрастает?
Вычислите эластичность спроса на товар
по цене
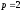 ,
дайте экономическое истолкование.
,
дайте экономическое истолкование.
-
Зависимость спроса от цены выражается формулой
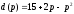 .
Вычислите эластичность спроса на товар
по цене
.
Вычислите эластичность спроса на товар
по цене
 ,
дайте экономическое истолкование.
Постройте график предельного спроса.
Запишите функцию выручки от цены. При
каких значениях цены выручка убывает?
,
дайте экономическое истолкование.
Постройте график предельного спроса.
Запишите функцию выручки от цены. При
каких значениях цены выручка убывает?
-
Пусть
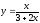 есть функция Торнквиста спроса
потребителей
есть функция Торнквиста спроса
потребителей
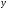 на товары первой необходимости в
зависимости от дохода
на товары первой необходимости в
зависимости от дохода
 .
Найдите эластичность
.
Найдите эластичность
 при
при
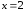 ,
дайте экономическое истолкование
полученному результату.
,
дайте экономическое истолкование
полученному результату.
-
Дана функция спроса
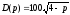 от цены товара
от цены товара
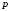 .
Составить функцию выручки. Вычислить
эластичность функции спроса в точке
.
Составить функцию выручки. Вычислить
эластичность функции спроса в точке
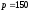 и дать экономическое истолкование
результату. Как повлияет изменение
цены на выручку?
и дать экономическое истолкование
результату. Как повлияет изменение
цены на выручку?
-
Предприятие производит
 ед. продукции в месяц и реализует ее по
цене
ед. продукции в месяц и реализует ее по
цене
 .
Суммарные издержки производства
составляют
.
Суммарные издержки производства
составляют
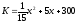 .
Определите, при каком объеме производства
прибыль предприятия будет максимальной.
.
Определите, при каком объеме производства
прибыль предприятия будет максимальной.
-
Производитель реализует свою продукцию по цене
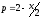 ден. ед. за единицу продукции, а издержки
задаются функцией
ден. ед. за единицу продукции, а издержки
задаются функцией
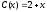 ,
где
,
где
 - объем выпущенной продукции. Найдите
оптимальный объем выпуска продукции
и соответствующую прибыль.
- объем выпущенной продукции. Найдите
оптимальный объем выпуска продукции
и соответствующую прибыль.
-
Поступления от реализации производственной продукции
 выражаются функцией
выражаются функцией
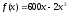 ,
а затраты, связанные с производством
продукции
,
а затраты, связанные с производством
продукции
 ,
записываются функцией
,
записываются функцией
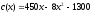 .
Определите оптимальный объем производства,
обеспечивающий максимум прибыли.
.
Определите оптимальный объем производства,
обеспечивающий максимум прибыли.
-
Производитель реализует свою продукцию по цене
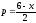 ден. ед. за единицу продукции, а издержки
задаются функцией
ден. ед. за единицу продукции, а издержки
задаются функцией
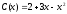 ,
где
,
где
 - объем выпущенной продукции. Найдите
оптимальный объем выпуска продукции
и соответствующую прибыль.
- объем выпущенной продукции. Найдите
оптимальный объем выпуска продукции
и соответствующую прибыль.
Задание 5
Задана функция Z=f(x,y), точка М0 (х0, у) и вектор ā = aх i + ау j. Требуется:
1)Вычислить производную функции в точке М0 в направлении вектора ā, указать смысл полученного результата.
2) Найти градиент функции в точки М0 и наибольшую скорость возрастания функции. Построить градиент.
5.1
U=x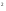 +y
+y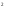 -2x+4y,
M
-2x+4y,
M (2,1),
(2,1),
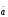 =2
=2 -
-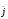 ,
,
5.2
U=x +y
+y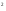 +4x+2y,
M
+4x+2y,
M (1,1),
(1,1),
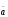 =3
=3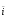 +2
+2 ,
,