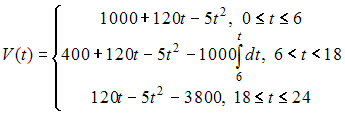Документ Microsoft Office Word (2)

  ЗАДАНИЕ N 28 отправить сообщение разработчикам Тема: Дифференциальные уравнения с разделяющимися переменными

Начало формы

Конец формы

Общее решение дифференциального уравнения  имеет вид …

Решение: Разделим переменные:  Проинтегрируем обе части уравнения:  Тогда  Откуда   где

  ЗАДАНИЕ N 29 отправить сообщение разработчикам Тема: Однородные дифференциальные уравнения первого порядка

Начало формы

Конец формы

Дифференциальное уравнение  заменой  приводится к уравнению с разделенными переменными, которое имеет вид …

Решение: Если  то  и Тогда уравнение  запишется в виде Преобразовав уравнение и разделив переменные, получим:

  ЗАДАНИЕ N 30 отправить сообщение разработчикам Тема: Линейные неоднородные дифференциальные уравнения первого порядка

Начало формы

Конец формы

Общее решение дифференциального уравнения  имеет вид …

Решение: Уравнение  перепишем в виде  Введем замену   Тогда уравнение  примет вид  или 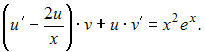Пусть  Тогда  Подставим найденное значение u в уравнение  Получим:   то есть  и  Окончательное решение имеет вид

  ЗАДАНИЕ N 31 отправить сообщение разработчикам Тема: Задача Коши для дифференциального уравнения первого порядка

Начало формы

Конец формы

Уравнение кривой, проходящей через точку  подкасательная которой в любой ее точке равна 4 имеет вид …

Решение: Подкасательная в произвольной точке равна  Тогда для нахождения уравнения искомой кривой получим уравнение 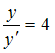 или  Проинтегрировав обе части этого уравнения, получим:   Для вычисления значения C подставим в найденное решение координаты точки  Тогда  и  Следовательно, уравнение кривой имеет вид

  ЗАДАНИЕ N 32 отправить сообщение разработчикам Тема: Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Начало формы

Конец формы

Функция  является частным решением линейного однородного дифференциального уравнения второго порядка …

Решение: Уравнение  не является линейным однородным дифференциальным уравнением второго порядка. Подставив  и  в уравнения  и  не получим тождества. Подставив  и  в уравнение  получим тождество. Следовательно, функция  является частным решением линейного однородного дифференциального уравнения второго порядка

  ЗАДАНИЕ N 33 отправить сообщение разработчикам Тема: Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Начало формы

Конец формы

Общий вид частного решения  линейного неоднородного дифференциального уравнения второго порядка  будет выглядеть как …

Решение: Общее решение этого уравнения можно записать в виде  где функция  – общее решение однородного уравнения  а функция  – некоторое частное решение исходного неоднородного уравнения. Для однородного уравнения составим характеристическое уравнение   и найдем его корни:  Тогда общее решение однородного уравнения будет иметь вид   Поскольку правая часть исходного уравнения  то имеем уравнение со специальной правой частью. Так как  является корнем характеристического уравнения, то частное решение  неоднородного уравнения будем искать в виде

  ЗАДАНИЕ N 34 отправить сообщение разработчикам Тема: Дифференциальные уравнения высших порядков, допускающие понижение порядка

Начало формы

Конец формы

Функция  является общим решением дифференциального уравнения второго порядка …

Решение: Найдем производные первого и второго порядков:   Подставляя функцию  и ее производные в уравнения ,  и  тождества не получим. При подстановке   и   в уравнение  получим тождество.Следовательно, функция  является общим решением дифференциального уравнения второго порядка

  ЗАДАНИЕ N 35 отправить сообщение разработчикам Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами

Начало формы

Конец формы

Общее решение системы дифференциальных уравнений  имеет вид …

Решение: Решим систему дифференциальных уравнений методом исключения. Из первого уравнения находим  тогда производная  и после подстановки выражений для  и  во второе уравнение системы получим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами  Характеристическое уравнение  имеет два действительных корня:  Таким корням соответствует общее решение однородного дифференциального уравнения Поскольку правая часть исходного уравнения  то имеем уравнение со специальной правой частью. Так как  не является корнем характеристического уравнения, то частное решение  неоднородного уравнения будем искать в виде Найдя производные первого и второго порядков и подставив в уравнение  получим Тогда общее решение этого уравнения имеет вид  Дифференцируя полученное решение, находим  и Значит, общее решение системы уравнений имеет вид

  ЗАДАНИЕ N 36 отправить сообщение разработчикам Кейс-задания: Кейс 1 подзадача 1

Начало формы

Конец формы

Для уборки снега на улицах города используются снегоуборочные машины. Они работают в течение светлого времени суток с 6 до 18 часов  с постоянной скоростью уборки снега 400  Изменение объема снега, выпадающего на улицы города в городе в течение суток, можно описать уравнением  где  – объем снега (в ), выпавшего за время t (в часах), В момент времени  на улицах города лежит 1000  снега. Пусть  – объем снега, лежащего на улицах города в момент времени t, тогда математическая модель для нахождения  может иметь вид …

Решение: Скорость изменения объема снега , лежащего на улицах города, для  равна  Учитывая, что в момент времени  на улицах города лежит 1000  снега, для  получим:  С 6 до 18 часов работают снегоуборочные машины с постоянной скоростью уборки снега 400 . Следовательно,  при  и После 18 часов снегоуборочные машины не работают. Следовательно,  при Поэтому

  ЗАДАНИЕ N 37 отправить сообщение разработчикам Кейс-задания: Кейс 1 подзадача 2

Начало формы

Конец формы

Для уборки снега на улицах города используются снегоуборочные машины. Они работают в течение светлого времени суток с 6 до 18 часов  с постоянной скоростью уборки снега 400  Изменение объема снега, выпадающего на улицы города в городе в течение суток, можно описать уравнением  где  – объем снега (в ), выпавшего за время t (в часах), В момент времени  на улицах города лежит 1000  снега. Установите соответствие между временем t и объемом снега, лежащего на улицах города 1. Объем снега, лежащего на улицах города в момент времени  часов. 2. Объем снега, лежащего на улицах города в момент времени  часов.