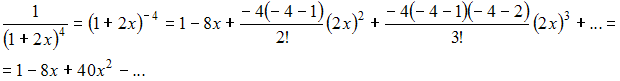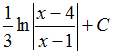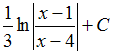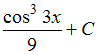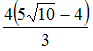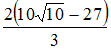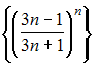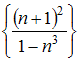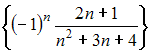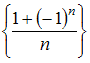Документ Microsoft Office Word
.docx



Конец формы
Множество
первообразных функции
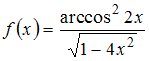 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Чтобы
определить множество первообразных,
вычислим неопределенный интеграл от
этой функции. Тогда
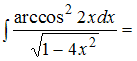 Произведем
замену
Произведем
замену
![]()
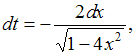
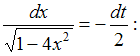
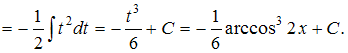
![]() ЗАДАНИЕ N 14
отправить
сообщение разработчикам
Тема:
Интегрирование по частям в неопределенном
интеграле
ЗАДАНИЕ N 14
отправить
сообщение разработчикам
Тема:
Интегрирование по частям в неопределенном
интеграле
Начало формы




Конец формы
Множество
первообразных функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Чтобы
определить множество первообразных,
вычислим неопределенный интеграл от
этой функции методом интегрирования
по частям по формуле
![]() Тогда
Тогда
![]()
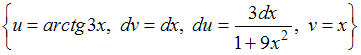
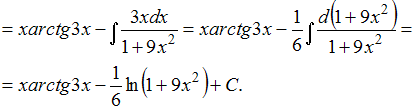
![]() ЗАДАНИЕ N 15
отправить
сообщение разработчикам
Тема:
Интегрирование рациональных функций
ЗАДАНИЕ N 15
отправить
сообщение разработчикам
Тема:
Интегрирование рациональных функций
Начало формы




Конец формы
Множество
первообразных функции
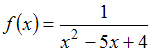 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Чтобы
определить множество первообразных,
вычислим неопределенный интеграл от
этой функции.
Разложив знаменатель
дробно-рациональной функции на линейные
множители, получаем
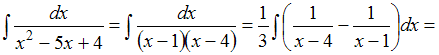
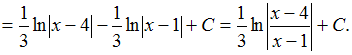
![]() ЗАДАНИЕ N 16
отправить
сообщение разработчикам
Тема:
Интегрирование иррациональных выражений
ЗАДАНИЕ N 16
отправить
сообщение разработчикам
Тема:
Интегрирование иррациональных выражений
Начало формы




Конец формы
Множество
первообразных функции
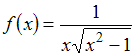 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Чтобы
определить множество первообразных,
вычислим неопределенный интеграл от
этой функции. Тогда
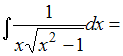 Произведем
замену
Произведем
замену
![]()
![]()
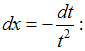
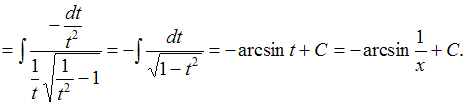
![]() ЗАДАНИЕ N 17
отправить
сообщение разработчикам
Тема:
Интегрирование тригонометрических
функций
ЗАДАНИЕ N 17
отправить
сообщение разработчикам
Тема:
Интегрирование тригонометрических
функций
Начало формы




Конец формы
Множество
первообразных функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Чтобы
определить множество первообразных,
вычислим неопределенный интеграл от
этой функции. Тогда
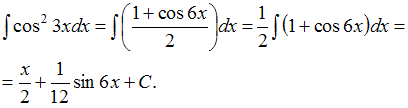
![]() ЗАДАНИЕ N 18
отправить
сообщение разработчикам
Тема:
Свойства определенного интеграла
ЗАДАНИЕ N 18
отправить
сообщение разработчикам
Тема:
Свойства определенного интеграла
Начало формы




Конец формы
Среднее
значение функции
![]() на
отрезке
на
отрезке
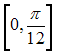 равно …
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Среднее
значение функции
![]() непрерывной
на отрезке
непрерывной
на отрезке
![]() вычисляется
по формуле
вычисляется
по формуле
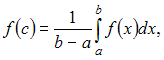 где
где
![]() Тогда
Тогда
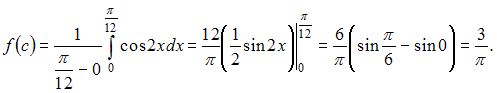
![]() ЗАДАНИЕ N 19
отправить
сообщение разработчикам
Тема:
Методы вычисления определенного
интеграла
ЗАДАНИЕ N 19
отправить
сообщение разработчикам
Тема:
Методы вычисления определенного
интеграла
Начало формы




Конец формы
Определенный
интеграл
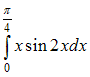 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Решение:
Для
вычисления данного определенного
интеграла применим формулу интегрирования
по частям:
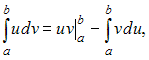 где
где
![]()
![]()
![]()
![]() Тогда
Тогда
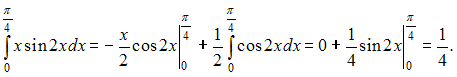
![]() ЗАДАНИЕ N 20
отправить
сообщение разработчикам
Тема:
Приложения определенного интеграла
ЗАДАНИЕ N 20
отправить
сообщение разработчикам
Тема:
Приложения определенного интеграла
Начало формы




Конец формы
Площадь
фигуры, изображенной на рисунке
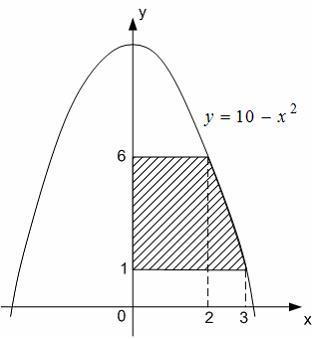 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Площадь
данной фигуры можно вычислить по формуле
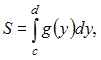 где
где
![]()
![]()
![]() Тогда
Тогда
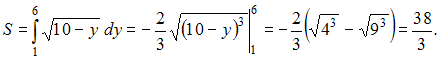
![]() ЗАДАНИЕ N 21
отправить
сообщение разработчикам
Тема:
Двойные интегралы
ЗАДАНИЕ N 21
отправить
сообщение разработчикам
Тема:
Двойные интегралы
Начало формы




Конец формы
Повторный
интеграл
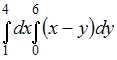 равен
…
равен
…
|
|
|
|
– 9 |
|
|
|
|
– 39 |
|
|
|
|
– 46,5 |
|
|
|
|
24 |
Решение:
Вычисление
повторного интеграла вида
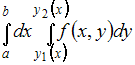 сводится
к последовательному вычислению
определенных интегралов с учетом того,
что при вычислении интеграла вида
сводится
к последовательному вычислению
определенных интегралов с учетом того,
что при вычислении интеграла вида
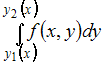 переменная
x
считается постоянной. Тогда
переменная
x
считается постоянной. Тогда
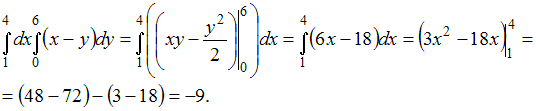
![]() ЗАДАНИЕ N 22
отправить
сообщение разработчикам
Тема:
Числовые последовательности
ЗАДАНИЕ N 22
отправить
сообщение разработчикам
Тема:
Числовые последовательности
Начало формы




Конец формы
Из
числовых последовательностей

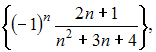
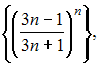
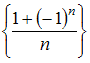 бесконечно
малой не
является
последовательность …
бесконечно
малой не
является
последовательность …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Бесконечно
малой последовательностью называется
последовательность
![]() предел
которой равен нулю, то есть
предел
которой равен нулю, то есть
![]() Рассмотрим
числовую последовательность
Рассмотрим
числовую последовательность
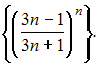 Так
как
Так
как
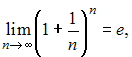 то
то
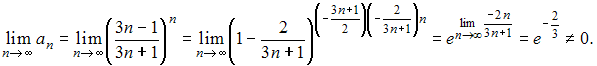 То
есть данная последовательность не
является бесконечно малой.
Остальные
последовательности являются бесконечно
малыми,
в чем легко убедиться, вычислив
пределы общего члена.
То
есть данная последовательность не
является бесконечно малой.
Остальные
последовательности являются бесконечно
малыми,
в чем легко убедиться, вычислив
пределы общего члена.
![]() ЗАДАНИЕ N 23
отправить
сообщение разработчикам
Тема:
Сходимость числовых рядов
ЗАДАНИЕ N 23
отправить
сообщение разработчикам
Тема:
Сходимость числовых рядов
Начало формы




Конец формы
Сумма
числового ряда
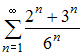 равна …
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
1 |
Решение:
Представим
общий член этого ряда в виде суммы
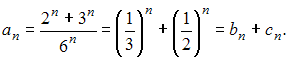 Тогда
ряды
Тогда
ряды
![]() и
и
![]() представляют
собой бесконечно убывающие геометрические
прогрессии. Следовательно, эти ряды
сходятся, причем:
представляют
собой бесконечно убывающие геометрические
прогрессии. Следовательно, эти ряды
сходятся, причем:
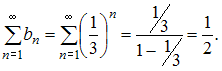
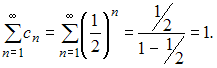 Таким
образом, сумма данного числового ряда
равна:
Таким
образом, сумма данного числового ряда
равна:
![]()
![]() ЗАДАНИЕ N 24
отправить
сообщение разработчикам
Тема:
Область сходимости степенного ряда
ЗАДАНИЕ N 24
отправить
сообщение разработчикам
Тема:
Область сходимости степенного ряда
Начало формы




Конец формы
Область
сходимости степенного ряда
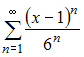 имеет
вид …
имеет
вид …
|
|
|
|
(– 5; 7) |
|
|
|
|
(– 6; 6) |
|
|
|
|
[– 5; 7) |
|
|
|
|
[– 6; 6) |
Решение:
Вычислим
предварительно радиус сходимости этого
ряда по формуле
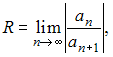 где
где
![]() Тогда
Тогда
![]() Следовательно,
интервал сходимости ряда имеет вид
Следовательно,
интервал сходимости ряда имеет вид
![]() ,
или
,
или
![]() .
Для
того чтобы найти область сходимости
степенного ряда, исследуем сходимость
ряда в граничных точках.
В точке x=
- 5 ряд примет вид
.
Для
того чтобы найти область сходимости
степенного ряда, исследуем сходимость
ряда в граничных точках.
В точке x=
- 5 ряд примет вид
![]() Данный
ряд расходится, так как
не выполняется
необходимое условие сходимости числового
ряда:
Данный
ряд расходится, так как
не выполняется
необходимое условие сходимости числового
ряда:
![]() В
точке x=7
получаем знакочередующийся ряд
В
точке x=7
получаем знакочередующийся ряд
![]() Аналогично
получаем
Аналогично
получаем
![]() то
есть ряд расходится.
Таким образом,
область сходимости ряда имеет вид
то
есть ряд расходится.
Таким образом,
область сходимости ряда имеет вид
![]()
![]() ЗАДАНИЕ N 25
отправить
сообщение разработчикам
Тема:
Ряд Тейлора (Маклорена)
ЗАДАНИЕ N 25
отправить
сообщение разработчикам
Тема:
Ряд Тейлора (Маклорена)
Начало формы




Конец формы
Если
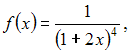 то
первые три (отличные от нуля) члена
разложения этой функции в ряд Маклорена
имеют вид …
то
первые три (отличные от нуля) члена
разложения этой функции в ряд Маклорена
имеют вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Из
разложения в ряд Маклорена функции
![]() следует,
что
следует,
что