Позиционные задачи на параллельность

Прямая параллельна плоскости, если она параллельна любой прямой, принадлежащей этой плоскости.

Две плоскости параллельны, если две пересекающиеся прямые одной плоскости взаимно параллельны двум пересекающимся прямым другой плоскости. На эпюре через точку К проведена плоскость, параллельная заданной.

Если две параллельные плоскости заданы следами, то одноименные следы этих плоскостей взаимно параллельны.

29

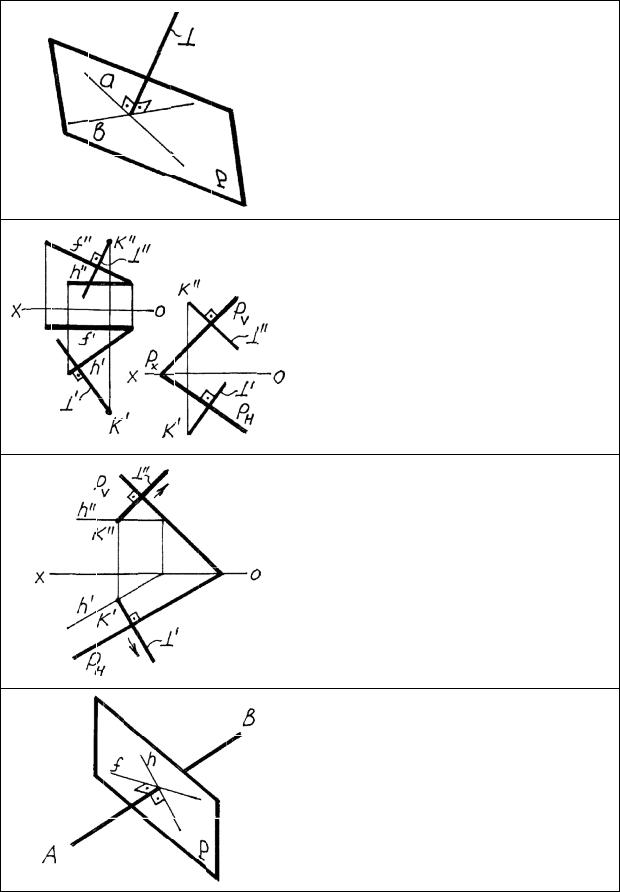
Проведение перпендикуляра к плоскости

Из элементарной геометрии известно: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. В качестве таких прямых наиболее целесообразно взять горизонталь и фронталь.

Проекции перпендикуляра к плоскости проводятся следующим образом: горизонтальная проекция перпендикуляра – перпендикулярно h/ или РH, фронтальная проекция – перпендикулярно f// или РV.

Если на плоскость опускают перпендикуляр или восстанавливают его из плоскости, то такая задача называется прямой задачей.

Если к прямой проводят плоскость, перпендикулярную заданной прямой, то такая задача называется обратной задачей. Она решается по тому же алгоритму, что и прямая задача.

30

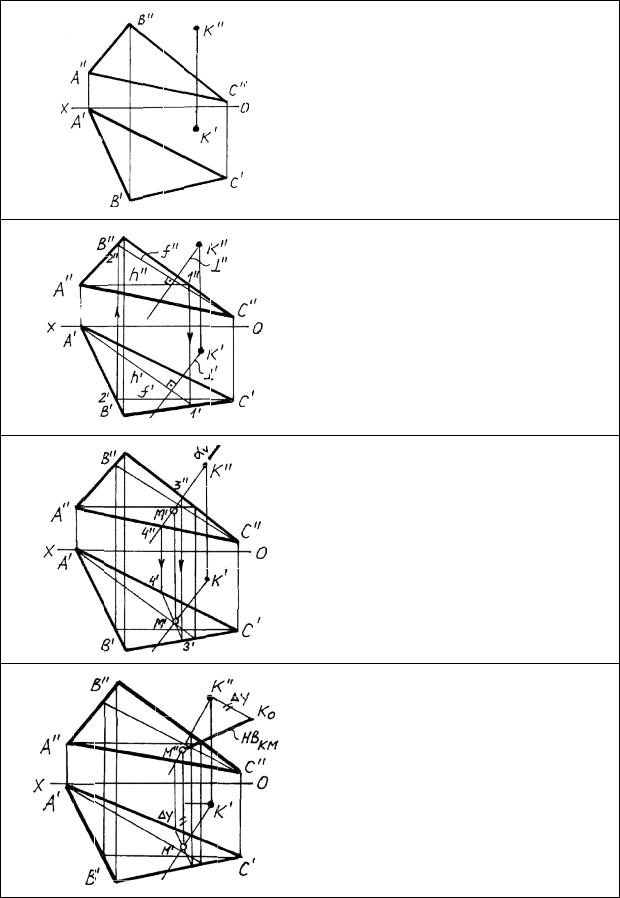
Определение расстояния от точки до плоскости

Требуется определить расстояние от точки до плоскости. Обший план решения задачи:

-опускаем из точки перпендикуляр на плоскость;

-находим точку встречи его с плоскостью;

-определяем натуральную величину расстояния.

Для того, чтобы опустить перпендикуляр на плоскость, проводим в ней горизонталь и фронталь. Далее из заданной точки проводим проекции перпендикуляра к плоскости согласно алгоритму -пер пендикулярности.

Находим точку встречи перпендикуляра с плоскостью. Это типовая задача о пересечении прямой с плоскостью (см. разд. «Пересечение прямой с плоскостью»).

Методом прямоугольного -тре угольника на любой из проекций перпендикуляра определяем натуральную величину расстояния от точки до плоскости.

31

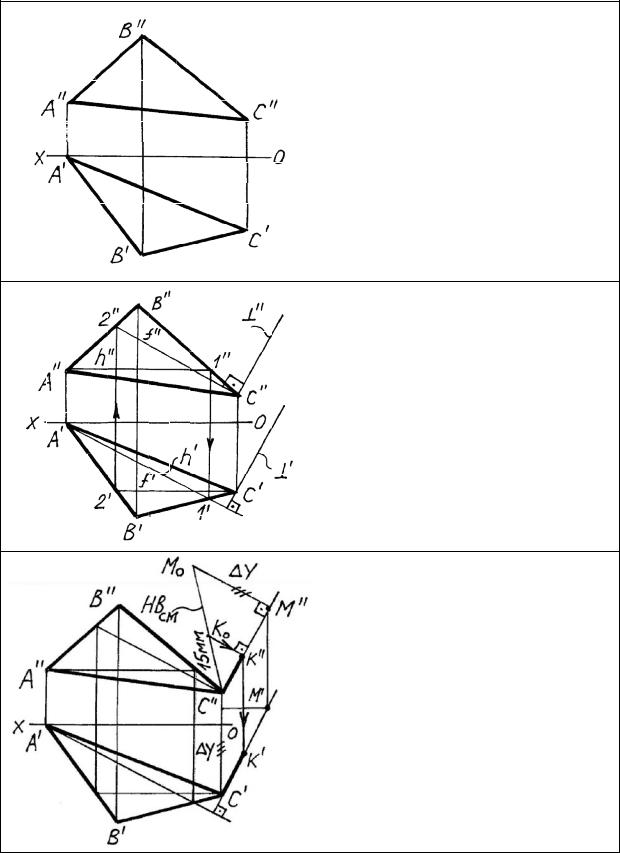
Восстановление перпендикуляра заданной длины

В плоскости треугольника проводим горизонталь и фронталь для того, чтобы восстановить из плоскости перпендикуляр и построить его проекции.

Ограничиваем перпендикуляр в произвольной точке М и определяем методом прямоугольного треугольника натуральную величину ограниченного отрезка перпендикуляра. Отмеряем на натуральной величине 15 мм и полученную точку K возвращаем на проекции перпендикуляра.

32