
- •Введение
- •Проекционный метод и виды проецирования
- •Инвариантные свойства (аксиомы) проецирования
- •Ортогональное проецирование на две и три плоскости проекций
- •Образование и свойства эпюра Монжа
- •Построение проекций точки по заданным координатам
- •Определение октанта по заданному эпюру точки
- •Построение недостающей проекции точки
- •Связь эпюра Монжа с проекционным чертежом
- •Прямые общего и частного положения
- •Построение следов прямой
- •Определение октантов, через которые проходит прямая
- •Метод прямоугольного треугольника
- •Теорема Фалеса и ее применение для решения задач
- •Определение видимости скрещивающихся прямых
- •Теорема прямого угла
- •Плоскости общего и частного положения
- •Проведение в плоскости горизонтали и фронтали
- •Линии наибольшего наклона (ЛНН) плоскости
- •Угол между плоскостью и плоскостью проекций
- •Позиционные задачи на принадлежность
- •Проведение через прямую вспомогательных плоскостей
- •Пересечение прямой с плоскостью
- •Позиционные задачи на пересечение плоскостей
- •Пересечение плоскостей, заданных плоскими фигурами
- •Определение видимости пересекающихся объектов
- •Позиционные задачи на параллельность
- •Проведение перпендикуляра к плоскости
- •Определение расстояния от точки до плоскости
- •Восстановление перпендикуляра заданной длины
- •Определение расстояния от точки до прямой
- •Перпендикулярность плоскостей
- •Метод замены плоскостей проекций
- •Первая типовая задача метода замены плоскостей проекций
- •Вторая типовая задача метода замены плоскостей проекций
- •Параметры вращения и методы преобразования эпюра вращением
- •Метод вращения вокруг проецирующих осей
- •Метод вращения вокруг линий уровня
- •Метод вращения плоскости вокруг следов и способы построения совмещенного следа
- •Методика решения задач способом совмещения
- •Метод плоско-параллельного перемещения (ППП)
- •Определение угла между прямой и плоскостью
- •Определение угла между плоскостями
- •Методы построения сечений многогранников
- •Построение разверток многогранников
- •Построение проекций особых точек на поверхности
- •Построение промежуточных точек на поверхности
- •Конические, цилиндрические и сферические сечения
- •Построение сечений поверхностей плоскостями частного положения
- •Построение сечений поверхностей плоскостями общего положения
- •Пересечение прямой с поверхностью (общий метод)
- •Построение линий пересечения поверхностей методом секущих вспомогательных плоскостей
- •Построение линий пересечения поверхностей методом секущих концентрических сфер
- •Теорема Монжа и ее использование для построения линий пересечения поверхностей
- •Построение разверток кривых поверхностей
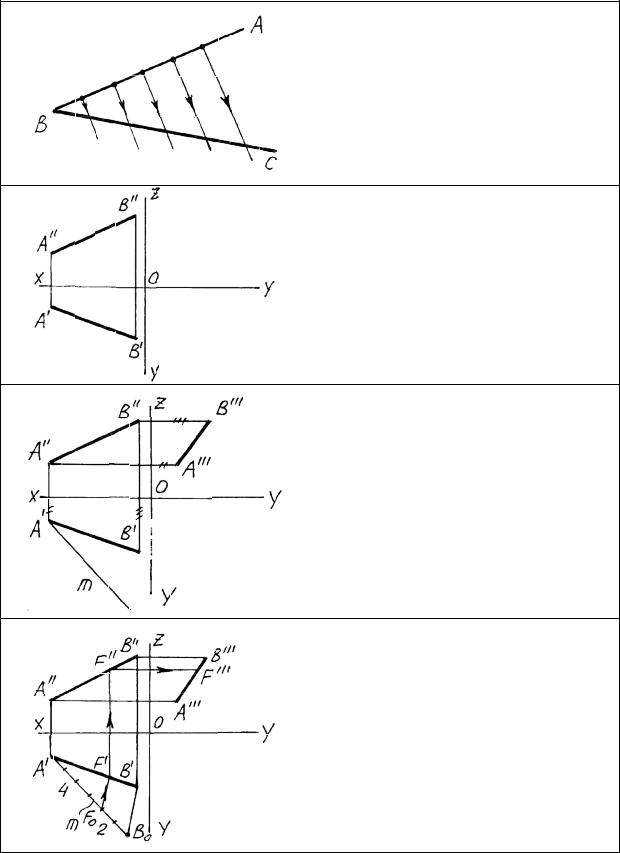
Теорема Фалеса и ее применение для решения задач
Из элементарной геометрии - из вестна теорема Фалеса: если на одной стороне угла отложить -рав ные или пропорциональные отрезки и через засечки провести - па раллельные прямые, то и другая сторона угла разделится на равные или пропорциональные отрезки.
Задача: разделить проекции прямой АВ в отношении 2:4, предварительно построив недостающую профильную проекцию.
Используя свойства эпюра Монжа, строим профильную проекцию прямой, для чего откладываем от оси OZ ординаты, замеренные на горизонтальной проекции прямой. Далее на любой проекции прямой, например на горизонтальной, проводим произвольную вспомогательную прямую m.
Откладываем на вспомогательной |
|
прямой 6 равных отрезков произ- |
|
вольной длины. Конец последнего |
|
отрезка |
соединяем с точкойВ/. |
На вспомогательной прямой -бе |
|
рем точку F0 и из нее параллельно |
|
отрезку |
В0В/ проводим линию |
связи, которая делит А/В/, а затем |
|
и другие проекции в заданном |
|
отношении. |
|
17
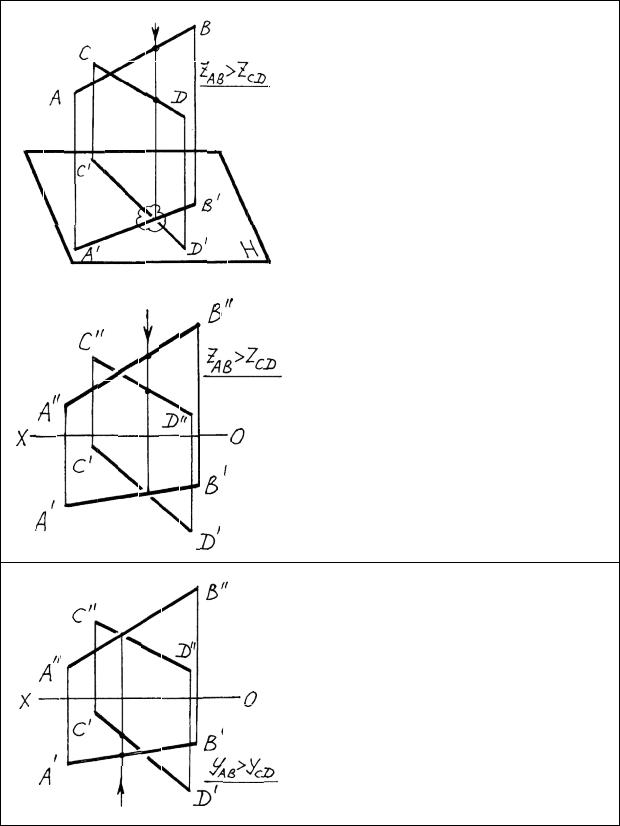
Определение видимости скрещивающихся прямых
При рассмотрении |
пространствен- |
|||
ного |
чертежа |
двух |
скрещиваю- |
|
щихся |
прямых |
можно |
сделать |
|
вывод: |
на горизонтальной |
проек- |
||
ции будет видна та прямая, кото- |
||||
рая имеет бóльшую аппликату в |
||||
конкурирующем месте. На фрон- |
||||
тальной проекции будет видна та |
||||
прямая, |
которая имеет бóльшую |
|||
ординату. На профильной проекции |
||||
будет видна прямая, имеющая бóль- |
||||
шую абсциссу. |
|
|
|
|
|
|
|||
Для определения видимости пря- |
||||
мых на проекциях необходимо: |
||||
-отметить конкурирующее место;
-провести через него линию связи;
-вдоль линии связи сравнить -ап пликаты скрещивающихся прямых, если определяется видимость на горизонтальной проекции;
-на рассматриваемой проекции будет видна та прямая, у которой больше аппликата (АВ).
На фронтальной проекции будет видна также прямая АВ, так как в конкурирующем месте у нее больше ордината. Метод определения видимости скрещивающихся прямых получил название метод конкурирующих точек, или метод конкурирующих прямых.
18
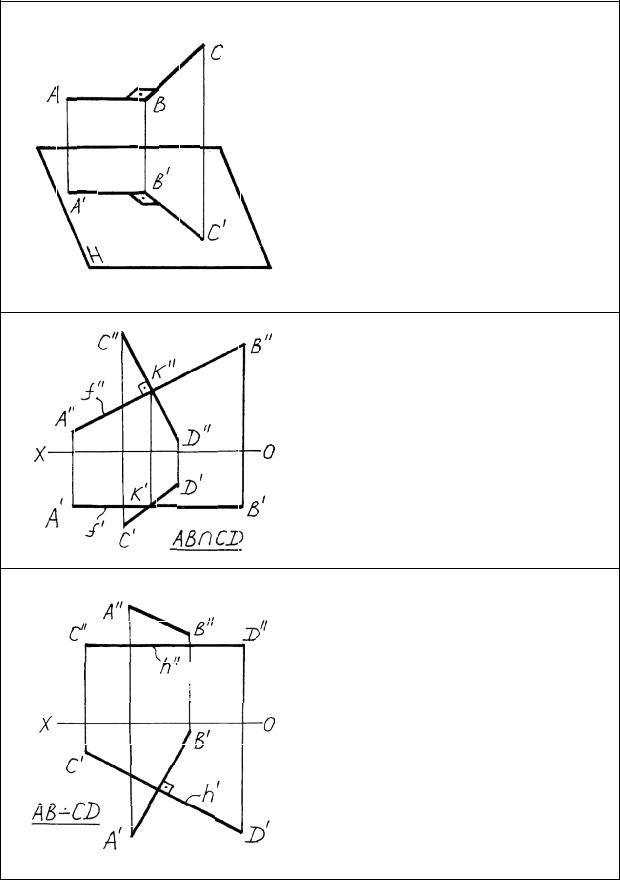
Теорема прямого угла
Прямой угол может быть спро- |
|||
ецирован |
в натуральную |
вели- |
|
чину, если его плоскость будет |
|||
параллельна |
плоскости |
проек- |
|
ций. Однако в соответствии с |
|||
теоремой |
прямой |
угол |
также |
проецируется без искажения, ес- |
|||
ли один из его катетов парал- |
|||
лелен плоскости проекций. Эта |
|||
теорема получила название тео- |
|||
ремы прямого угла и широко ис- |
|||
пользуется в геометрических -за |
|||
дачах. |
|
|
|
На эпюре |
показано использова- |
ние теоремы прямого угла для |
|
построения проекций двух пере- |
|
секающихся |
перпендикулярных |
прямых, одна из которых явля- |
|
ется фронталью. |
|
Теорема прямого угла распространяется не только на пересекающиеся перпендикулярные прямые, но и на скрещивающиеся перпендикулярные прямые.
19
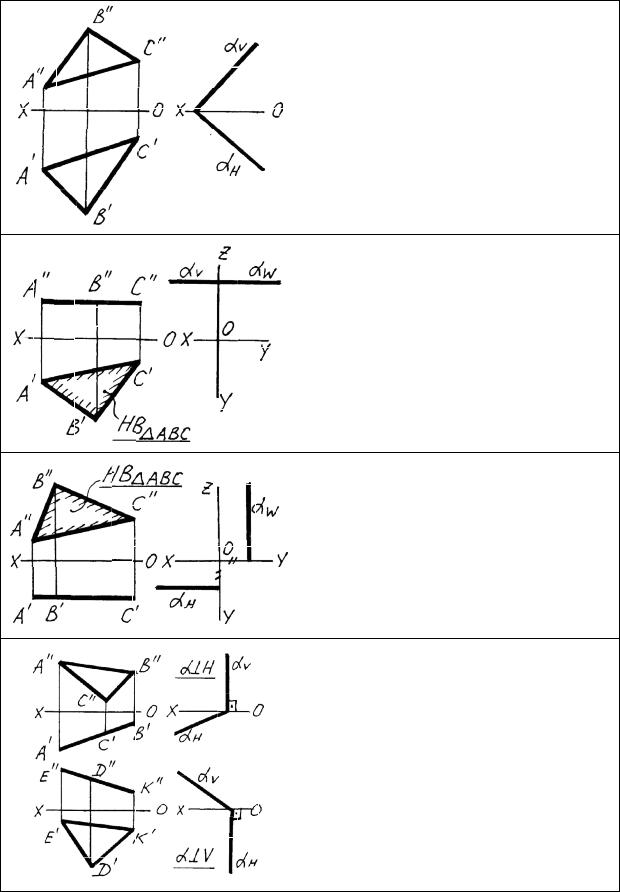
Плоскости общего и частного положения
Плоскость общего положения – это плоскость, не параллельная и не перпендикулярная ни одной из плоскостей проекций. Признак плоскости общего положения на эпюре – ни одна проекция плоскости (ни один след) не параллельна, не перпендикулярна осям проекций и ни на одной проекции плоскость не «выродилась» в прямую.
Плоскости, параллельные или перпендикулярные плоскостям проекций, называются плоскостями частного положения. Горизонтальная плоскость параллельна плоскости H. Главный признак плоскости на эпюре – фронтальная проекция «вырождается» в линию, параллельную оси ОХ.
Фронтальная |
плоскость |
парал- |
лельна плоскости V. На эпюре |
ее |
|
горизонтальная |
проекция «вы- |
|
рождается» в |
линию, параллель- |
|
ную ОХ. Следы горизонтальной и |
||
фронтальной |
плоскостей |
парал- |
лельны оси ОХ. |
|
|
Плоскости, перпендикулярные плоскостям проекций, называются проецирующими. По аналогии с прямой различают горизонтально-, фронтально- и профильно-проецирую- щие плоскости. Главный признак проецирующих плоскостей на эпюре – на одной из проекций плоскость «вырождается» в линию. Проецирующие следы перпендикулярны соответствующим осям.
20
