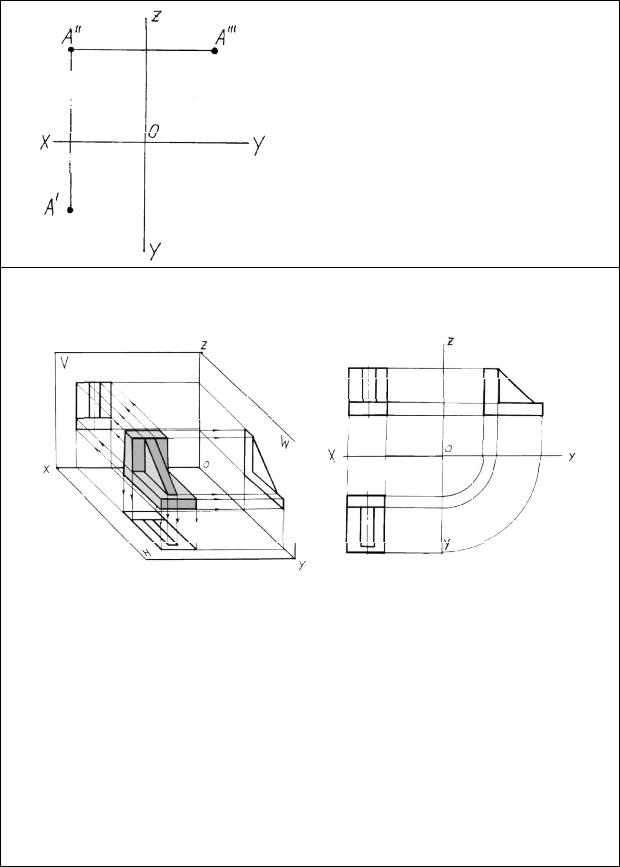
Связь эпюра Монжа с проекционным чертежом

Эпюр Монжа является универсальным способом изображения геометрических объектов на плоскости. Он позволяет не только изобразить объект в проекциях, но и определить его положение в пространстве. Основными проекциями объекта являются:

А/ - горизонтальная проекция; А// - фронтальная проекция; А/// - профильная проекция.

Горизонтальная проекция объекта – вид сверху

В проекционном черчении эпюр Монжа является теоретической основой для составления чертежа детали. В отличие от эпюра Монжа

впроекционном черчении проекции называют видами:

-А/ - вид сверху;

-А// - вид спереди;

-А/// - вид слева.

Все свойства эпюра Монжа на чертеже сохраняются.

13

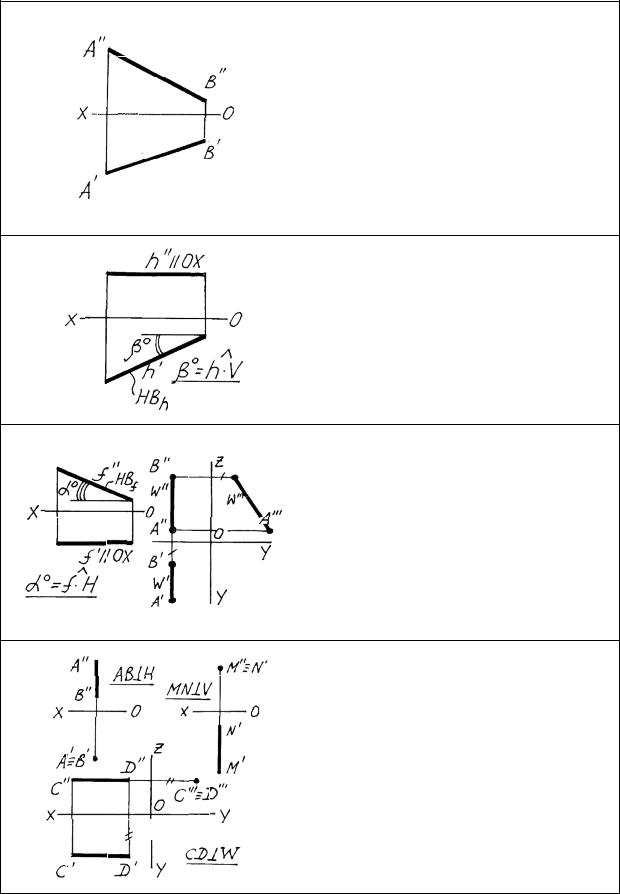
Прямые общего и частного положения

Прямой общего положения называется прямая, не параллельная и не перпендикулярная ни одной из плоскостей проекций. Признаком прямой общего положения на эпюре является то, что ни одна проекция прямой не параллельна, не перпендикулярна осям проекций и ни на одной проекции прямая не «выродилась» в точку.

Прямые, параллельные или перпендикулярные плоскостям проекций, называются прямыми частного положения. Горизонталь – это прямая, параллельная горизонтальной плоскости проекций. Главный признак горизонтали на эпюре – h// всегда параллельна оси ОХ.

Прямые, перпендикулярные плоскостям проекций, называются проецирующими. В зависимости от того, к какой плоскости проекций прямая перпендикулярна, различают горизонтально-, фронтально- и профильно-проецирующие прямые. Главный признак проецирующих прямых на эпюре – на одной из проекций прямая«вырождается» в точку.

14

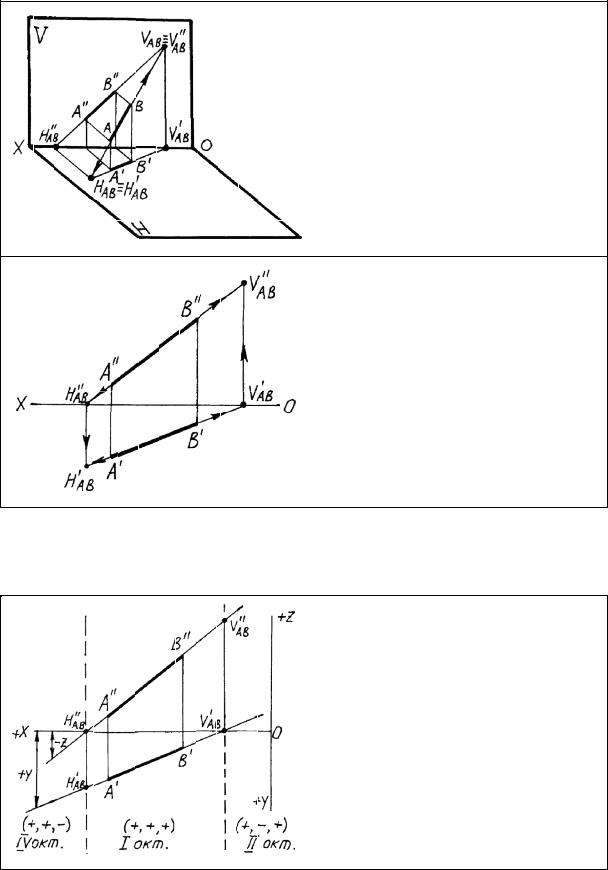
Построение следов прямой

Следами прямой называют точки пересечения прямой с плоскостями проекций. На пространственном макете представлены построения следов и их проекций. Различают горизонтальный, фронтальный и профильный следы.

На эпюре представлено построение проекций горизонтального и фронтального следов прямой.

Определение октантов, через которые проходит прямая

В точках следов прямая переходит из одного октанта в другой. Номера октантов можно определить по знакам координат прямой на участках прямой между следами и за их пределами.

15

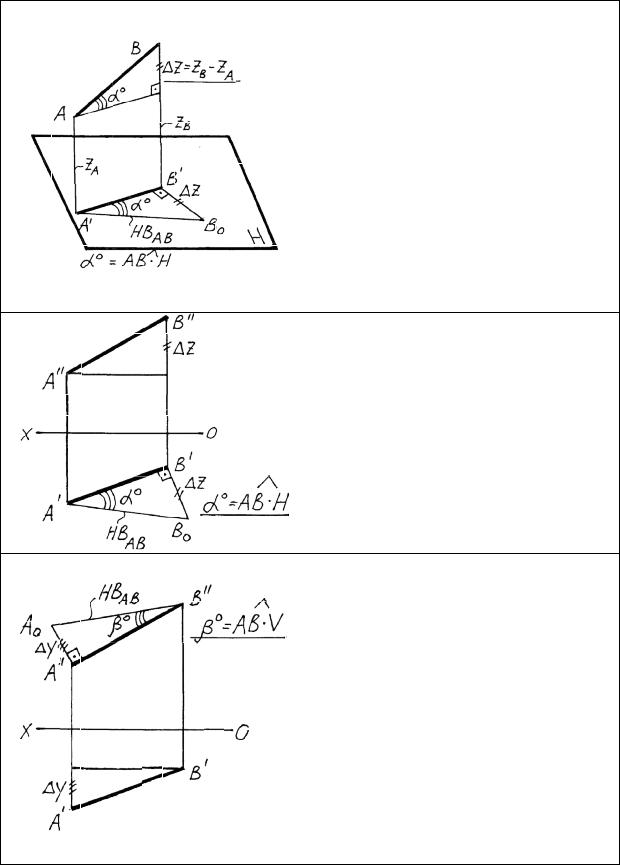
Метод прямоугольного треугольника

Если прямоугольный треугольник строится на фронтальной проекции, то на катете откладывают разность ординат; если – на профильной, то – разность абсцисс. В первом случае дополнительно определяется угол наклона пря-

мой к фронтальной плоскости проекций, во втором – угол наклона прямой к профильной плоскости проекций.

16