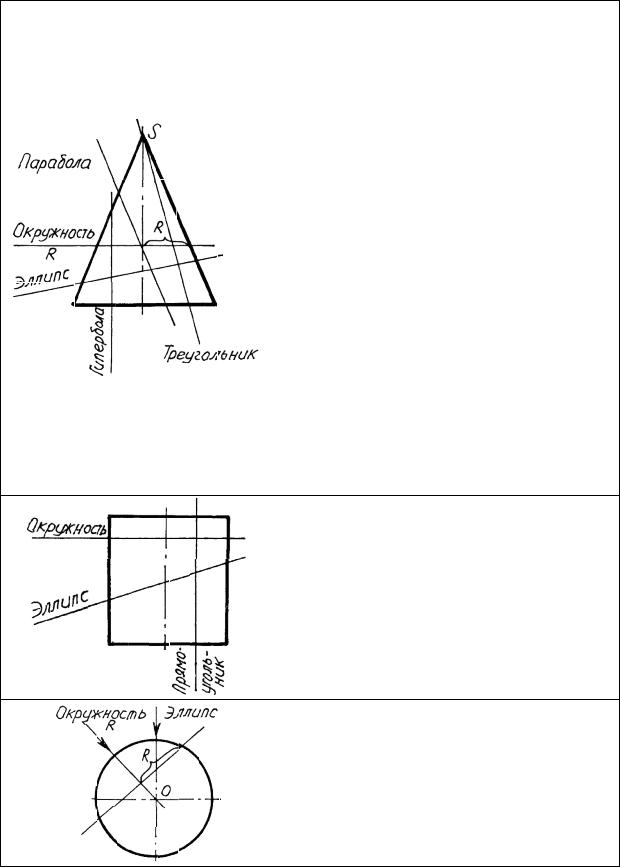
Конические, цилиндрические и сферические сечения

Прямой круговой конус является поверхностью, имеющей большое количество разнообразных сечений. Если секущая плоскость перпендикулярна оси, то в сечении образуется окружность. Если секущая плоскость -на клонна к оси и пересекает обе образующие, то в сечении будет эллипс. При пересечении конуса плоскостью, параллельной оси, в сечении получается гипербола. Парабола образуется в сечении конуса, если секущая плоскость параллельна образующей. Если плоскость проходит через вершину, то сечением конуса является треугольник. Плоскости, образующие в сечении конуса наиболее простые фигуры (окружность известного радиуса и треугольник), при решении различных геометрических задач используются в качестве вспомогательных.

В сечении прямого кругового цилиндра образуется окружность, если секущая плоскость перпендикулярна оси цилиндра. Если секущая плоскость не перпендикулярна оси, то в сечении будет эллипс. В сечении цилиндра образуется прямоугольник, если плоскость параллельна оси.

Всякое сечение сферы есть окружность, если направление проецирования перпендикулярно плоскости сечения, и эллипс, если это условие не соблюдается.

49

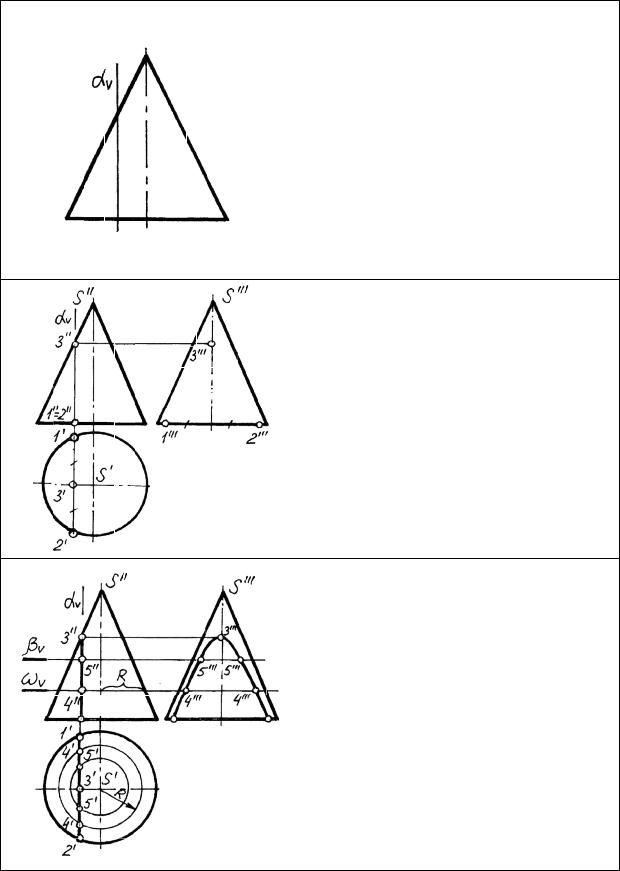
Построение сечений поверхностей плоскостями частного положения

Поверхность может быть рассечена плоскостями частного и общего положения. Наиболее эффективным методом построения сечений поверхностей является метод -се кущих вспомогательных плоскостей. Он включает в себя ряд последовательных логических действий. Рассмотрим пример построения сечения конуса плоскостью частного положения.

Находим характерные точки и строим их проекции. Характерными точками являются точки, в которых секущая плоскость пересекает оси, очерковые образующие, основания. В данном примере это точки 1, 2 и 3. Проекции этих точек строим с использова-

нием свойства эпюра Монжа:

АXА/ = АZА///.

50

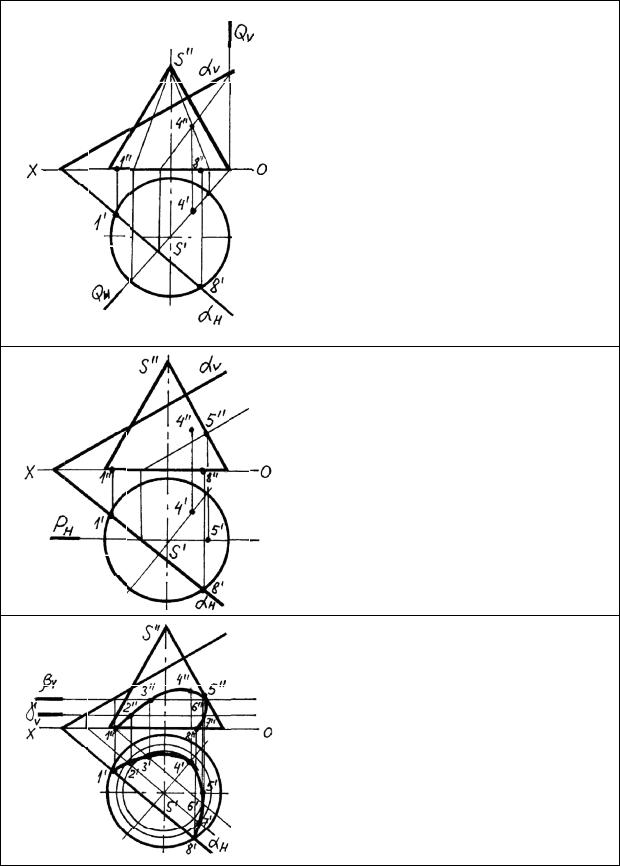
Построение сечений поверхностей плоскостями общего положения

Рассмотрим построение сечения конуса плоскостью общего положения. Характерными точками являются точки 1, 8, в которых след пересекает окружность основания конуса, так как они лежат в одной плоскости Н. Наивысшую точку сечения найдем с помощью вспомогательной плоскости Q, проходящей через вершину конуса. В сечении конуса плоскостью Q будет треугольник. Построим линию пересечения заданной плоскости и плоскости Q. На пересечении этих элементов найдем высшую точку 4.

Точку касания линии сечения с очерковой образующей найдем аналогично с помощью вспомогательной плоскости Р.

Промежуточные точки 2, 3, 6 и 7 найдем методом секущих вспомогательных плоскостей, в качестве которых используем горизонтальные плоскости. Полученные точки соединяем плавной линией.

51

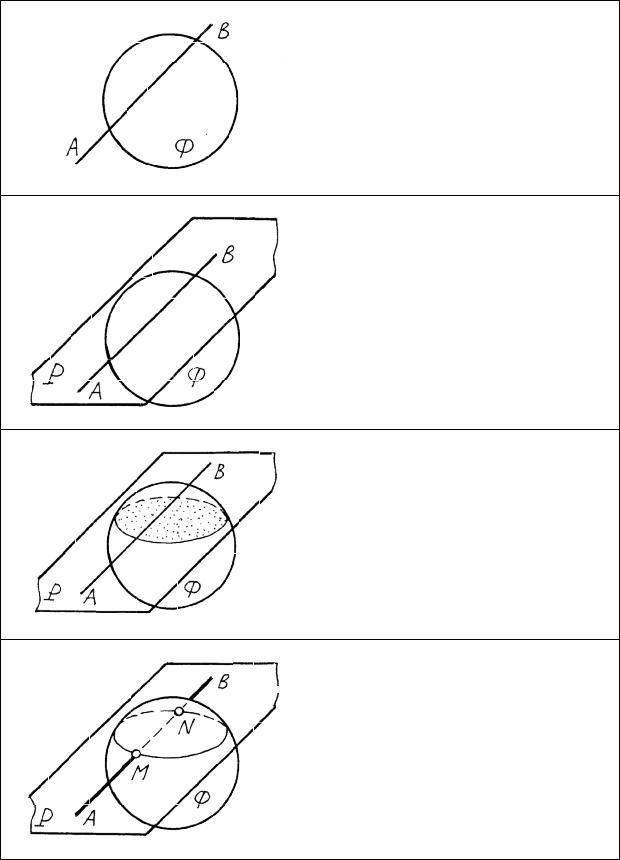
Пересечение прямой с поверхностью (общий метод)

Задана поверхность Ф.

Требуется найти точки пересечения (или точки встречи) прямой АВ с поверхностью.

Проводим через прямую вспомогательную плоскость Р. В качестве вспомогательной плоскости наиболее целесообразно взять такую плоскость общего или частного положения, которая в сечении поверхности образовывала бы наиболее простые фигуры, например, многоугольник или окружность.

Строим сечение поверхности вспомогательной плоскостью Р.

Находим общие точки заданной прямой и контура построенного сечения. Полученные точки М и N являются искомыми.

52

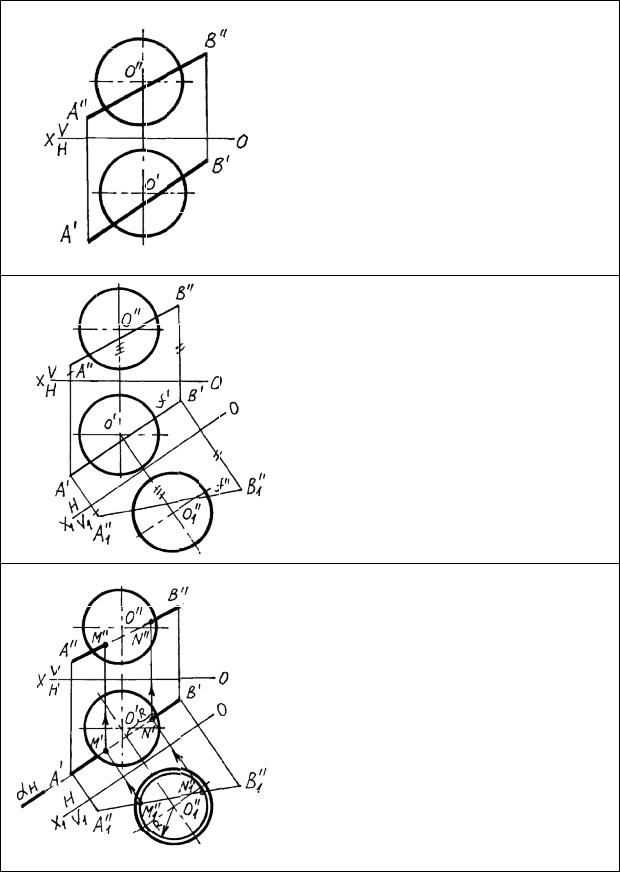
Пересечение прямой с поверхностью методом преобразования эпюра

При решении задач на пересечение прямой с поверхностью в некоторых случаях целесообразно использовать методы преобразования с тем, чтобы перевести прямую общего положения в частную, что позволяет упростить решение задач. Этот прием эффективен, если поверхностью является, например, сфера.

Рассмотрим пересечение прямой общего положения со сферой.

Решим задачу методом перемены плоскостей проекций. Произведем замену V→V1. Новую ось расположим параллельно горизонтальной проекции прямой. Во второй системе плоскостей проекций прямая занимает положение фронтали.

Проводим через прямую вспомогательную плоскость. Затем построим сечение сферы вспомогательной плоскостью. В сечении будет окружность радиуса R. Полученные точки встречи прямой с поверхностью возвращаем на исходные проекции.

53