4. Последовательности, списки, множества. Массивы. Вектора.

В системе Maple любые выражения могут включаться в наборы, относящиеся кмножественным данным. Такие наборы в виде множеств создаются с помощью фигурных скобок { }:

> {a,b,a,a,b,d,e,c,d};

{a, b, с, е, d}

> {10,2+3,4+4,8,5,1};

{1, 5, 8, 10}

> {`Hello` ,`my`,`friend`};

{friend, Hello, my}

Отличительная черта множеств — автоматическое устранение из них повторяющихся по значению элементов. Кроме того, Maple расставляет элементы множеств в определенном порядке — числа в порядке увеличения значения, а символы и строки в алфавитном порядке. Для множеств нет строгого математического определения, и мы будем считать их наборами, удовлетворяющими перечисленным выше признакам.

Для создания упорядоченных наборов — списков — служат квадратные скобки []:

> [10,2+3,4+4,8,5,1];

[10, 5, 8, 8, 5, 1]

> [а, b, c, a, a, d, d, e] ;

[a, b, с, a, a, d, d, e]

Как нетрудно заметить, элементы списков преобразуются и выводятся строго в том порядке, в каком они были заданы. Списки широко применяются для задания векторов и матриц.

В ряде случаев, например, при подготовке данных для двумерных графиков, возникает необходимость в подготовке парных списков — скажем, координат точек (х, у) графика. Для этого можно использовать функцию zip(f, u, v) или zip(f, u, v, d). Здесь f — бинарная функция, u, v — списки или векторы, d — необязательное значение.

Примеры применения функции zip даны на рис. 2.5. Там же показано применение этих средств для построения точек, представляющих множество действительных чисел на плоскости. Для этого использована функция pointplot из пакета plots.

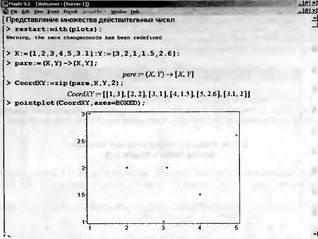
Рис. 2.5. Представление множества чисел на плоскости

Создание массивов, векторов и матриц

Важным типом данных являются списки или листы. В Maple 9.5 они создаются с помощью квадратных скобок, например:

[1,2,3,4] — список из четырех целых чисел;

[1,2.34,5] — список из двух вещественных и одного целого числа;

[a,b, "Привет"] — список из двух символов (переменных) и строковой константы;

[sin(x), 2*cos(x),a^2-b] — список из трех математических выражений.

Для создания векторов (одномерных массивов) и матриц (двумерных массивов) служит функция array. Обычно она используется в следующих формах:

array[a..b,s1] — возвращает вектор с индексами от а до b и значениями в одномерном списке s1;

array[a..b,c..d,s2] — возвращает матрицу с номерами строк от а до b, номерами столбцов от с до d и значениями в двумерном списке s2.

Примеры задания вектора и матрицы представлены ниже:

array(1..3,[х,у,х+у]) — создает вектор с элементами x, у и х+y;

array(1..2,1..2,[[a,b],[c,d]]) — квадратная матрица 

Для создания векторов может использоваться также конструктор векторов Vector[o](d, init, ro, sh, st, dt, f, а, о) с рядом опционально заданных параметров. В этой книге эта конструкция практически не используется. Векторы и матрицы можно также задавать с помощью угловых скобок:

> V:=<a,b,с>;

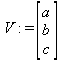
> Vector[row]([a,b,с]);

[a, b, c]

> Vector[row](<a, b, c>);

[a, b, c]

> M:=<<a,b,c>|<d,e,f>>;

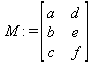
Имеется множество функций для работы со списками, массивами и матрицами. Они будут рассмотрены в дальнейшем. В принципе, размерность массивов, создаваемых списками, не ограничена, и массивы могут быть многомерными.