
3 уровень
Тема 1 : Метрические и топологические пространства
Вопрос № 1
|
V3 |
Функция d(x, y ), определяющая метрику на множестве действительных чисел |
|
1 |
| x- y | |
|
1 |
| x3 – y3 | |
|
1 |
| arctg x – arctg y| |
|
0 |
( x2 + 3y2 ) | x – y| |
|
0 |
| x2 – y2 | |
|
0 |
| sin ( x-y)| |
|
0 |
x3 – y3 |
|
0 |
| tg (x-y)| |
Вопрос № 2
|
V3 |
Метрическое пространство - |
|
1 |
Любое
множество М
|
|
1 |
Любое линейное нормированное пространство с метрикой d (x, y) = || x – y || |
|
1 |
Числовая
прямая с метрикой d(x,
y)
=
|
|
0 |
Числовая
прямая с метрикой d(x,
y)
=
|
|
0 |
Множество рациональных чисел с метрикой d ( x, y ) = x – y |
|
0 |
Множество иррациональных чисел с метрикой d ( x, y ) =sin ( x – y) |
|
0 |
Числовая прямая с метрикой d(x, y) = x2 – y2 |
|
0 |
Любое
множество М
|
Вопрос № 3
|
V3 |
Метрическое пространство ( здесь x=( x1, x2) , y = (y1, y2) ) - |
|
1 |
Любое
множество М
|
|
1 |
Любое линейное нормированное пространство с метрикой d (x, y) = || x – y || |
|
1 |
Множество
точек плоскости с метрикой d
(x,
y
)=
|
|
0 |
Множество точек плоскости с рациональными координатами и с метрикой d (x, y )= (x1 + y1 ) + (x2 + y2 ) |
|
0 |
Множество точек плоскости с иррациональными координатами и с метрикой d ( x, y ) = ( x1 – y1 ) + ( x2 – y 2) |
|
0 |
Множество
М
|
|
0 |
Множество точек плоскости с метрикой d (x, y ) = sin (x1 - y1 ) + sin (x2 - y2 ) |
|
0 |
Множество точек плоскости с метрикой d (x, y ) = cos (x1 - y1 )2 + cos (x2 - y2 )2 |
Вопрос № 4
|
V3 |
Метрическое пространство - |
|
1 |
Множество
непрерывных на [ a;
b]
функций с метрикой
d(x,
y)
=
|
|
1 |
Любое линейное нормированное пространство с метрикой d (x, y) = || x – y || |
|
1 |
Множество
непрерывных на [ a;
b]
функций с метрикой
d(x,
y)
=
|
|
0 |
Множество многочленов с метрикой d (P1, P2) = | P1(0) - P2 ( 0) | |
|
0 |
Множество непрерывных на [ a; b] функций с метрикой d(x, y) = x (t ) – y(t) |
|
0 |
Множество монотонных функций с метрикой d(x, y) = x (a ) ∙ y(a) |
|
0 |
Множество
непрерывно дифференцируемых на [ a;
b]
функций с метрикой
d(x,
y)
=
|
|
0 |
Множество непрерывных на [ a; b] функций с метрикой d(x, y) = | x (b ) – y(a) | |
Вопрос № 5
|
V3 |
Замыкание множества Е |
|
1 |
Операция присоединения к Е всех его предельных точек |
|
1 |
Пересечение всех замкнутых множеств, содержащих Е |
|
1 |
Наименьшее замкнутое множество, содержащее Е |
|
0 |
Любое открытое множество этого пространства содержит другое непустое открытое множество, целиком свободное от точек множества А |
|
0 |
Внутренность замыкания А равно пустому множеству |
|
0 |
Объединение всех открытых множеств, содержащих Е |
|
0 |
Операция удаления внутренних точек |
|
0 |
Наибольшее открытое множество, содержащее Е |
Вопрос № 6
|
V3 |
Свойства операции замыкания |
|
1 |
A
|
|
1 |
|
|
1 |
|
|
0 |
A
|
|
0 |
|
|
0 |
|
|
0 |
|
|
0 |
|
Вопрос № 7
|
V3 |
Множество Е всюду плотно в Х, если |
|
1 |
|
|
1 |
Каждая точка множества Х является либо предельной точкой множества Е, либо принадлежит множеству Е ( либо и то, и другое) |
|
1 |
Замыкание множества Е совпадает со всем пространством Х |
|
0 |
ограничено |
|
0 |
Не ограничено |
|
0 |
замкнутое |
|
0 |
открытое |
|
0 |
конечное |
Вопрос № 8
|
V3 |
Нигде не плотное множество А в метрическом пространстве Х |
|
1 |
Любое открытое множество этого пространства содержит другое непустое открытое множество, целиком свободное от точек множества А |
|
1 |
Внутренность замыкания А равно пустому множеству |
|
1 |
Не плотно ни в одном шаре, т.е. если в каждом шаре содержится другой шар, не имеющий с Е ни одной общей точки |
|
0 |
Пересечение всех замкнутых множеств, содержащих Е |
|
0 |
Наименьшее замкнутое множество, содержащее Е |
|
0 |
Объединение всех открытых множеств, содержащих Е |
|
0 |
Наибольшее открытое множество, содержащее Е |
|
0 |
Операция присоединения к Е всех его предельных точек |
Вопрос № 9
|
V3 |
Множество, нигде не плотное на координатной плоскости R2 |
|
1 |
прямая |
|
1 |
Отрезок |
|
1 |
окружность |
|
0 |
Обе координаты которых рациональны |
|
0 |
Обе координаты которых иррациональны |
|
0 |
Одна из координат которых рациональна |
|
0 |
Обе координаты которых действительны |
|
0 |
Одна координата рациональна, другая иррациональна |
Вопрос № 10
|
V3 |
Множество, всюду плотное на координатной плоскости R2 |
|
1 |
Обе координаты которых рациональны |
|
1 |
Обе координаты которых иррациональны |
|
1 |
Одна из координат которых рациональна |
|
0 |
Обе координаты которых целые |
|
0 |
Одна координата целая |
|
0 |
Точки окружности x2 + y2 = 1 |
|
0 |
Точки замкнутого круга x2 + y2 ≤ 1 |
|
0 |
Точки открытого круга x2 + y2 < 1 |
Вопрос № 11
|
V3 |
Множество, нигде не плотное на числовой прямой |
|
1 |
Канторово множество |
|
1 |
Множество натуральных чисел |
|
1 |
{ ½, ¼, 1/8, 1/16, …} |
|
0 |
Множество рациональных чисел |
|
0 |
Множество иррациональных чисел |
|
0 |
[0; 4] |
|
0 |
Множество действительных чисел |
|
0 |
Множество рациональных чисел сегмента [0; 4] |
Вопрос № 12
|
V3 |
Всюду плотное множество в пространстве C[a; b] – это множество |
|
1 |
всех многочленов с рациональными коэффициентами |
|
1 |
всех многочленов |
|
1 |
всех многочленов с иррациональными коэффициентами |
|
0 |
Канторово |
|
0 |
Линейных функций |
|
0 |
Ограниченных функций |
|
0 |
Разрывных функций |
|
0 |
Интегрируемых функций |
Вопрос № 13
|
V3 |
Всюду плотное множество в пространстве Lp[a; b] – это множество |
|
1 |
всех многочленов с рациональными коэффициентами |
|
1 |
всех многочленов |
|
1 |
всех непрерывных функций |
|
0 |
Канторово |
|
0 |
Линейных функций |
|
0 |
Ограниченных функций |
|
0 |
Разрывных функций |
|
0 |
неограниченных |

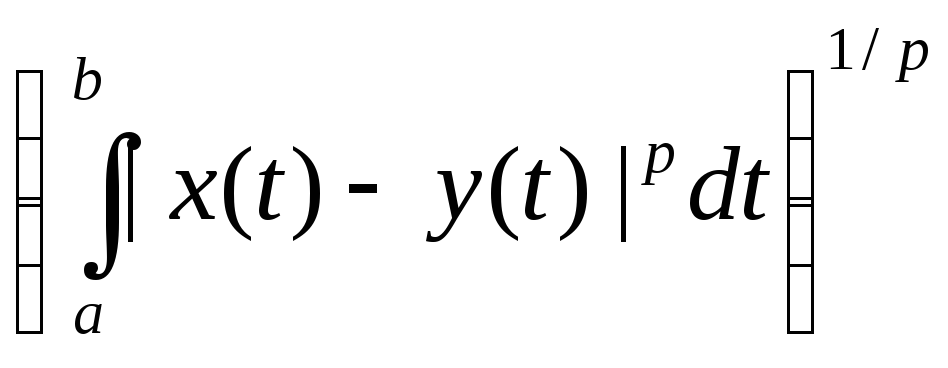 , 1 ≤p
<
, 1 ≤p
<