
- •1)Электростатика. Закон кулона и область его применения.
- •2)Напряженность и потенциал электрического поля. Связь между ними. Энергия взаимодействия системы зарядов.
- •3)Теорема Гаусса.
- •4)Диполь. Поле Диполя. Диполь в электрическом поле.
- •5)Электростатические явления в веществе.
- •6)Вектор электрической индукции :
- •7)Уравнения Максвела для электростатического поля в веществе.
- •8) Сегнетоэлектрики :
- •9)Проводники в электрическом поле.
- •10)Электроёмкость уединенного проводника.
- •11) Конденсаторы :
- •12) Энергия заряженного проводника.
- •14) Постоянный электрический ток
- •15)Эдс и Закон Ома :
- •16) Работа и мощность тока
- •17) Магнитное поле в вакууме
- •18)Закон Био-Савара-Лапласа.
- •19)Сила Лоренца
- •20)Сила Ампера :
- •20) Уравнения Максвелла в системе уравнений магнитостатики и электростатики
- •21) Магнитное поле в веществе.
- •22) Напряженность магнитного поля
- •23)Условия для h и b на границе раздела двух изотропных магнетиков :
- •24)Контур с током в магнитном поле :
- •25)Диамагнетики :
- •25)Пармагнетизм :
- •27) Ферромагнетики и антиферромагнетики :
- •28)Энергия магнитного поля :
- •29)Нестационарные явления в теории электромагнетизма :
- •30)Самоиндукция. Взаимная индукция. Индуктивность.
- •31)Токи замыкания и размыкания цепи :
- •32)Вихревое электрическое поле. Токи Фуко.
- •33)Электромагнитные волны как следствие из уравнений Максвела.
- •34)Предмет оптики. Геометрическая оптика.
- •35)Интерференция световых волн :
- •36)Опыт Юнга. Зеркала Френеля.
- •37)Интерференция в тонких плёнках.
- •38)Дифракция света.
- •39) Дифракция Френеля на круглом отверстии:
- •40)Дифракция Фраунгофера от щели :
- •41)Характеристики спектральных приборов.
- •42)Поляризация света :
- •43)Двойное лучепреломление.
- •44)Дисперсия света.
- •45) Тепловое излучение
- •Закон Стефана — Больцмана
- •Закон Вина
22) Напряженность магнитного поля
Она необходима для определения магнитной индукции поля, создаваемого токами различной конфигурации в различных средах.Напряженность магнитного поляхарактеризует магнитное поле в вакууме.
Напряженность магнитного поля (формула) векторная физическая величина, равная:
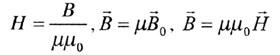
Где
u0- магнитная постоянная.![]() Гн/м
Гн/м![]() Н/А².
Н/А².
Напряженность магнитного поляв СИ - ампер на метр (А/м).
Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению. Если знать Напряженность магнитного поля в данной точке, то можно определить индукцию поля в этой точке.
Напряженность магнитного полязависит только от силы тока, протекающего по проводнику, и его геометрии.
С помощью следующей формулы, мы можем сформулировать теорему о циркуляции вектора H:циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макроскопических токов, охватываемых этим контуром.
![]()
![]()
Напряженность магнитного поля является аналогом электрического смещения.
23)Условия для h и b на границе раздела двух изотропных магнетиков :
Рассмотрим поведение линий векторов магнитной индукции и напряжённости магнитного поля при переходе через границу раздела двух магнетиков.
Представим
себе две однородные, изотропные
полубесконечные среды с магнитными
проницаемостями
![]() и
и![]() ,
имеющие плоскую горизонтальную границу
раздела. Пусть оба магнетика находятся
в однородном внешнем магнитном поле.
Чтобы понять, как происходит преломление
линий векторов магнитной индукции
,
имеющие плоскую горизонтальную границу
раздела. Пусть оба магнетика находятся
в однородном внешнем магнитном поле.
Чтобы понять, как происходит преломление
линий векторов магнитной индукции![]() и
напряжённости магнитного поля
и
напряжённости магнитного поля![]() через
эту границу, рассмотрим проекции этих
векторов на саму границу и на направление,
перпендикулярное границе и назовём их
касательными и нормальными составляющими,
соответственно.
через
эту границу, рассмотрим проекции этих
векторов на саму границу и на направление,
перпендикулярное границе и назовём их
касательными и нормальными составляющими,
соответственно.
Пусть
![]() и
и![]() ─
нормальные составляющие векторов
магнитной индукции и напряжённости
магнитного поля, а
─
нормальные составляющие векторов
магнитной индукции и напряжённости
магнитного поля, а![]() и
и![]() ─
касательные составляющие тех же векторов
в верхней среде, имеющей магнитную
проницаемость
─
касательные составляющие тех же векторов
в верхней среде, имеющей магнитную
проницаемость![]() .
Аналогичные величины в нижней среде,
имеющей магнитную проницаемость
.
Аналогичные величины в нижней среде,
имеющей магнитную проницаемость![]() ,
обозначим
,
обозначим![]()
![]()
![]()
![]() .
.
Представим
себе, что линии вектора
![]() преломляются
при переходе через границу раздела так,
как показано на рис. 1. Рассмотрим при
этом преломление пока только одной
силовой линии.
преломляются
при переходе через границу раздела так,
как показано на рис. 1. Рассмотрим при
этом преломление пока только одной
силовой линии.
Поместим
на границе раздела воображаемую
цилиндрическую поверхность с высотой
h
значительно меньшей радиусов оснований
S1
и S2,
лежащих по обе стороны от границы раздела
и параллельных ей. На рисунке также
показана нормаль
![]() к
границе раздела и к обоим основаниям.
к
границе раздела и к обоим основаниям.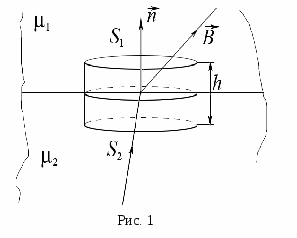
Запишем теорему Гаусса для магнитной индукции:
![]() или
или
![]() ,
,
где S ─ замкнутая поверхность, состоящая из боковой поверхности и оснований цилиндра.
Этот круговой интеграл можно разбить на 3 интеграла, каждый из которых равен потоку через верхнее и нижнее основания и боковую поверхность
![]() .
.
Здесь
![]() и
и![]() ─
нормальные составляющие векторов
магнитной индукции в верхнем и нижнем
магнетиках, соответственно,
─
нормальные составляющие векторов
магнитной индукции в верхнем и нижнем
магнетиках, соответственно,![]() ─
среднее значение проекции вектора
магнитной индукции на нормаль к боковой
поверхности.
─
среднее значение проекции вектора
магнитной индукции на нормаль к боковой
поверхности.
Поскольку оба магнетика помещены в однородное внешнее магнитное поле, то все интегралы можно заменить соответствующими произведениями:
![]() .
.
Как
и в предыдущей формуле, здесь первая
составляющая магнитного потока
![]() положительна,
так как силовые линии выходят из
поверхности
положительна,
так как силовые линии выходят из
поверхности![]() ,
а вторая составляющая
,
а вторая составляющая![]() ─
отрицательна, так как силовые линии
входят в поверхность
─
отрицательна, так как силовые линии
входят в поверхность![]() (вектора
(вектора![]() и
и![]() спроектированы
на одну и ту же нормаль). Третьей
составляющей ─
спроектированы
на одну и ту же нормаль). Третьей
составляющей ─![]() можно
пренебречь, так как высота цилиндра
выбрана очень малой по сравнению с
радиусами оснований, т. е., если
можно
пренебречь, так как высота цилиндра
выбрана очень малой по сравнению с
радиусами оснований, т. е., если![]() ,
то
,
то![]() .
.
Учитывая,
что
![]() ,
получим:
,
получим:
![]() .
(1)
.
(1)
Используя связь магнитной индукции и напряжённости магнитного поля
![]() ,
(2)
,
(2)
и, применяя её для первого и второго магнетиков в формуле (1), получим:
![]() .
.
Отсюда следует
![]() .
(3)
.
(3)
