20)Сила Ампера :

Как нам уже известно, магнитное поле оказывает на рамку с током ориентирующее действие. Значит, вращающий момент, который испытывает рамка, является результатом действия сил на отдельные ее элементы. Сравнивая и обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер открыл, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, который находится в магнитном поле, равна

(1) где dl - вектор, по модулю равный dl и совпадающий по направлению с током, В - вектор магнитной индукции. Направление вектора dF может быть определено, используя (1), по правилу векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, которая действует на ток

Модуль силы Ампера (см. (1)) равен

(2)

где α — угол между векторами dl и В.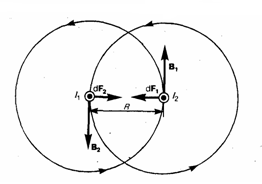

Закон Ампера используется при нахождении силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I₁ и I₂; (направления токов даны на рис. 1), расстояние между которыми R. Каждый из проводников создает вокруг себя магнитное поле, которое действует по закону Ампера на соседний проводник с током. Найдем, с какой силой действует магнитное поле тока I₁ на элемент dl второго проводника с током I₂. Магнитное поле тока I₁ есть линии магнитной индукции, представляющие собой концентрические окружности. Направление вектора B₁ задается правилом правого винта, его модуль по формуле (5) есть

Направление силы dF₁, с которой поле B₁ действует на участок dl второго тока, находится по правилу левой руки и указано на рисунке. Модуль силы, используя (2), с учетом того, что угол α между элементами тока I₂ и вектором B₁ прямой, будет равен подставляя значение дляВ₁, найдем

(3) Аналогично рассуждая, можно показать, что сила dF₂ с которой магнитное поле тока I₂ действует на элемент dl первого проводника с током I₁, направлена в противоположную сторону и по модулю равна

(4) Сопоставление выражений (3) и (4) дает, что

т. е.два параллельных тока одинакового направления притягиваются друг к другу с силой, равной (5) Еслитоки имеют противоположные направления, то, используя правило левой руки, определим, что между ними действует сила отталкивания, определяемая выражением (5).

20) Уравнения Максвелла в системе уравнений магнитостатики и электростатики

         Так как на практике почти всегда приходится решать уравнения Максвелла (1) – (4) в кусочно-непрерывных средах, то граничные условия (24) следует рассматривать как неотъёмлемую часть уравнений Максвелла (1) – (4).

         В случае стационарных электрических и магнитных полей (и) система уравнений Максвелла (1) – (4) распадается на систему

уравнений электростатики:

                                           ,      ,(25)

и уравнений магнитостатики:

                                          ,     ,,                                (26)

а граничные условия остаются те же

21) Магнитное поле в веществе.

До сих пор рассматривалось магнитное поле, которое создавалось проводниками с током или движущимися электрическими зарядами, находящимися в вакууме. Если же магнитное поле создается не в вакууме, а в какой-то другой среде, то магнитное поле изменяется. Это объясняется тем, что различные вещества, помещенные в магнитное поле, намагничиваются и сами становятся источниками магнитного поля. Вещества, способные намагничиваться в магнитном поле, называются магнетиками. Намагниченное вещество создает магнитное поле с индукцией , которое накладывается на магнитное поле с индукцией, обусловленное токами. Оба поля в сумме дают результирующее поле, магнитная индукция которого равна

.

Под действием поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается – его суммарный магнитный момент становится отличным от нуля. Магнитные поля отдельных молекулярных токов в этом случае уже не компенсируют друг друга и возникает поле В'.

Намагничениемагнетика естественно характеризовать магнитным моментом единицы объема. Эту величину называют вектором намагничивания и обозначают J. Если магнетик намагничен неоднородно, вектор намагничения в данной точке определяется следующим выражением:(43.2)

где ΔV–физически бесконечно малый объем, взятый в окрестности рассматриваемой точки, рm – магнитный момент отдельной молекулы. Суммирование производится по всем молекулам, заключенным в объеме ΔV.

Магнитный моменттока это произведение площади контура, в котором он протекает на силу тока в нем. Магнитный момент направлен перпендикулярно плоскости контура. Это направление можно определить с помощью правила буравчика. Если буравчик вращать по направлению движения тока в контуре, то его поступательное движение укажет направление магнитного момента.

В случае плоского контура с электрическим током магнитный момент вычисляется как

,

где —сила токав контуре,— площадь контура,— единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.