
- •1)Электростатика. Закон кулона и область его применения.
- •2)Напряженность и потенциал электрического поля. Связь между ними. Энергия взаимодействия системы зарядов.
- •3)Теорема Гаусса.
- •4)Диполь. Поле Диполя. Диполь в электрическом поле.
- •5)Электростатические явления в веществе.
- •6)Вектор электрической индукции :
- •7)Уравнения Максвела для электростатического поля в веществе.
- •8) Сегнетоэлектрики :
- •9)Проводники в электрическом поле.
- •10)Электроёмкость уединенного проводника.
- •11) Конденсаторы :
- •12) Энергия заряженного проводника.
- •14) Постоянный электрический ток
- •15)Эдс и Закон Ома :
- •16) Работа и мощность тока
- •17) Магнитное поле в вакууме
- •18)Закон Био-Савара-Лапласа.
- •19)Сила Лоренца
- •20)Сила Ампера :
- •20) Уравнения Максвелла в системе уравнений магнитостатики и электростатики
- •21) Магнитное поле в веществе.
- •22) Напряженность магнитного поля
- •23)Условия для h и b на границе раздела двух изотропных магнетиков :
- •24)Контур с током в магнитном поле :
- •25)Диамагнетики :
- •25)Пармагнетизм :
- •27) Ферромагнетики и антиферромагнетики :
- •28)Энергия магнитного поля :
- •29)Нестационарные явления в теории электромагнетизма :
- •30)Самоиндукция. Взаимная индукция. Индуктивность.
- •31)Токи замыкания и размыкания цепи :
- •32)Вихревое электрическое поле. Токи Фуко.
- •33)Электромагнитные волны как следствие из уравнений Максвела.
- •34)Предмет оптики. Геометрическая оптика.
- •35)Интерференция световых волн :
- •36)Опыт Юнга. Зеркала Френеля.
- •37)Интерференция в тонких плёнках.
- •38)Дифракция света.
- •39) Дифракция Френеля на круглом отверстии:
- •40)Дифракция Фраунгофера от щели :
- •41)Характеристики спектральных приборов.
- •42)Поляризация света :
- •43)Двойное лучепреломление.
- •44)Дисперсия света.
- •45) Тепловое излучение
- •Закон Стефана — Больцмана
- •Закон Вина
18)Закон Био-Савара-Лапласа.
Определяет величину модуля вектора магнитной индукции в точке выбранной произвольно находящейся в магнитном поле. Поле при этом создано постоянным током на некотором участке.
Закон
Био-Савара-Лапласа
для проводника с током I, элемент dl
которого создает в некоторой точке
индукциюполя
dB,
равен![]() (1)где dl
- вектор, по модулю равный длине dl
элемента проводника и совпадающий по
направлению с током, r
- радиус-вектор, который проведен из
элемента dl
проводника в точку А поля, r - модуль
радиуса-вектора r.
Направление dB
перпендикулярно dl
и r,
т. е. перпендикулярно плоскости, в которой
они лежат, и совпадает с направлением
касательной к линии магнитной индукции.
Это направление может быть найдено по
правилу правого винта: направление
вращения головки винта дает направление
dB,
если поступательное движение винта
совпадает с направлением тока в элементе.
Модуль вектора
dB
задается выражением
(1)где dl
- вектор, по модулю равный длине dl
элемента проводника и совпадающий по
направлению с током, r
- радиус-вектор, который проведен из
элемента dl
проводника в точку А поля, r - модуль
радиуса-вектора r.
Направление dB
перпендикулярно dl
и r,
т. е. перпендикулярно плоскости, в которой
они лежат, и совпадает с направлением
касательной к линии магнитной индукции.
Это направление может быть найдено по
правилу правого винта: направление
вращения головки винта дает направление
dB,
если поступательное движение винта
совпадает с направлением тока в элементе.
Модуль вектора
dB
задается выражением![]() (2)где α — угол
между векторами dl
и r.
(2)где α — угол
между векторами dl
и r.
Магнитное поле кругового тока
Определим индукцию поля в центре О кругового тока по формуле
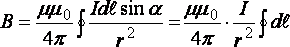 .
.
Так
как
![]() ,
а
,
а![]() и
и![]() –
постоянные;
–
постоянные;![]() ,
так как сумма всех элементарных отрезков
,
так как сумма всех элементарных отрезков![]() составляет
длину окружности.
составляет
длину окружности.
Следовательно,

Магнитное поле проводника конечной длины с током.
Рассчитаем индукцию магнитного поля В, создаваемую в точке А (рис. 2.2) на расстоянии r0 от прямолинейного проводника с током:

;
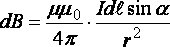 ;
;
 .
(2.4)
.
(2.4)
Выразим
переменные
![]() и.
Из рис. 2.2 видно, что
и.
Из рис. 2.2 видно, что
![]() .
Дифференцируя это выражение, получаем:
.
Дифференцируя это выражение, получаем:
 .
.
Из рис. 2.2 так же следует, что
 .
.
Подставляя
значения
![]() иr
в уравнение (2.4), имеем:
иr
в уравнение (2.4), имеем:
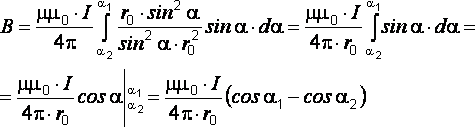
 .
.
19)Сила Лоренца
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика Х. Лоренца (1853 — 1928) — основателя электронной теории строения вещества. Силу Лоренца можно найти с помощью закона Ампера.
Рассмотрим
отрезок тонкого прямого проводника с
током. Пусть длина отрезка Δl
и площадь поперечного сечения проводника
S
настолько малы, что вектор индукции
магнитного поля
![]() можно
считать одинаковым в пределах этого
отрезка проводника. Сила токаI
в проводнике связана с зарядом частиц
q,
концентрацией заряженных частиц n
(числом зарядов в единице объема) и
скоростью их упорядоченного движения
v
следующей формулой:
можно
считать одинаковым в пределах этого
отрезка проводника. Сила токаI
в проводнике связана с зарядом частиц
q,
концентрацией заряженных частиц n
(числом зарядов в единице объема) и
скоростью их упорядоченного движения
v
следующей формулой:
I = qnvS ( 2 )
Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен:
F = | I |B Δl sin α
Подставляя в эту формулу выражение ( 2 ) для силы тока, получаем:
F = | q | nvS Δl B sin α = v | q | NB sin α,
где N = nSΔl — произведение равное числу носителей тока, содержащихся в элементе тока dl. Разделив dF на это число, найдем силу F ,действующую на заряд q движущийся со скоростью v.
![]()
Сила Лоренца перпендикулярна векторам магнитной индукции и скорости упорядоченного движения заряженных частиц. Ее направление определяется с помощью того же правила левой руки, что и направление силы Ампера.
Движение частиц в однородном магнитном поле :
Для
вывода общих закономерностей будем
полагать, что магнитное поле однородно
и на частицы не действуют электрические
поля. Если заряженная частица в магнитном
поле движется со скоростью v
вдоль линий магнитной индукции, то угол
α между векторами v
и В
равен 0 или π. Тогда сила Лоренца равна
нулю, т. е. магнитное поле на частицу не
действует и она движется равномерно и
прямолинейно.
1)В случае, если
заряженная частица движется в магнитном
поле со скоростью v,
которая перпендикулярна вектору В,
то сила Лоренца F=Q[vB]
постоянна по модулю и перпендикулярна
к траектории частицы. По второму закону
Ньютона, сила Лоренца создает
центростремительное ускорение. Значит,
что частица будет двигаться по окружности,
радиус r которой находится из условия
QvB=mv2/r
, следовательно
![]() (1)
(1)
 Период
вращения частицы,
т. е. время Т, за которое она совершает
один полный оборот,
Период
вращения частицы,
т. е. время Т, за которое она совершает
один полный оборот,
![]() Подставив
(1), получим
Подставив
(1), получим![]() (2)
т. е. период вращения частицы в
однородном магнитном поле задается
только величиной, которая обратна
удельному заряду (Q/m) частицы, и магнитной
индукцией поля, но при этом не зависит
от ее скорости (при v<<c). На этом
соображении основано действие циклических
ускорителей заряженных частиц.
2)В
случае, если скоростьv
заряженной частицы направлена под углом
α к вектору В
,то ее движение можно задать в виде
суперпозиции: 1) прямолинейного
равномерного движения вдоль поля со
скоростью vparall=vcosα
; 2) равномерного движения со скоростью
vperpend=vsinα
по окружности в плоскости, которая
перпендикулярна полю. Радиус окружности
задается формулой (1) (в этом случае надо
вместо v
подставить vperpend=vsinα).
В результате сложения двух данных
движений возникает движение по спирали,
ось которой параллельна магнитному
полю (рис. 1). Шаг винтовой (спиральной)
линии
(2)
т. е. период вращения частицы в
однородном магнитном поле задается
только величиной, которая обратна
удельному заряду (Q/m) частицы, и магнитной
индукцией поля, но при этом не зависит
от ее скорости (при v<<c). На этом
соображении основано действие циклических
ускорителей заряженных частиц.
2)В
случае, если скоростьv
заряженной частицы направлена под углом
α к вектору В
,то ее движение можно задать в виде
суперпозиции: 1) прямолинейного
равномерного движения вдоль поля со
скоростью vparall=vcosα
; 2) равномерного движения со скоростью
vperpend=vsinα
по окружности в плоскости, которая
перпендикулярна полю. Радиус окружности
задается формулой (1) (в этом случае надо
вместо v
подставить vperpend=vsinα).
В результате сложения двух данных
движений возникает движение по спирали,
ось которой параллельна магнитному
полю (рис. 1). Шаг винтовой (спиральной)
линии![]()

Подставив
в данное выражение (2), найдем
![]() Направление,
в котором закручивается спираль,
определяется знаком заряда частицы.
Если скоростьvзаряженной частицы
составляет угол α с направлением вектораВнеоднородного магнитного поля,
у которого индукция возрастает в
направлении движения частицы, то r и h
уменьшаются с увеличениемВ. На этом
основана фокусировка заряженных частиц
в магнитном поле.
Направление,
в котором закручивается спираль,
определяется знаком заряда частицы.
Если скоростьvзаряженной частицы
составляет угол α с направлением вектораВнеоднородного магнитного поля,
у которого индукция возрастает в
направлении движения частицы, то r и h
уменьшаются с увеличениемВ. На этом
основана фокусировка заряженных частиц
в магнитном поле.
