
- •Практикум
- •Занятие 7.
- •Задачи для самостоятельного решения
- •Занятие №9.
- •Правило Лопиталя.
- •Производная функции, заданной параметрически.
- •Примеры
- •Как определять интервалы выпуклости (вогнутости) и точки перегиба графика функции:
- •Задачи для самостоятельного решения
- •Перечень вариантов домашней контрольной работы по теме «Исследование функций и построение их графиков»
- •Список литературы
- •Скворцова Мария Ивановна Мудракова Ольга Александровна Кротов Герман Сергеевич
Задачи для самостоятельного решения
Найти интервалы возрастания, убывания функции и экстремумы
а)
![]() ;б)
;б)
![]() ;в)
;в)
![]() .
.
Найти интервалы выпуклости, вогнутости и точки перегиба графика функции:
а)
![]() ;б)
;б)
![]() ;в)
;в)
![]() .
.
Найти асимптоты графика функции:
а)
![]() ;б)
;б)
![]() ;в)
;в)
![]() .
.
Ответы
а) Функция
 возрастает при
возрастает при ,
убывает при
,
убывает при ;
; — точка минимума.
— точка минимума.
б)
Функция
![]() возрастает при
возрастает при![]() ,
убывает при
,
убывает при![]() ;
;![]() — точка минимума;
— точка минимума;![]() — точка разрыва.
— точка разрыва.
в)
Функция
![]() возрастает при
возрастает при![]() ,
убывает при
,
убывает при![]() ;
;![]() — точка максимума,
— точка максимума,![]() — точка минимума.
— точка минимума.
2)
а) График функции
![]() выпуклый при
выпуклый при![]() ,
вогнутый при
,
вогнутый при![]() ;
;![]() — точка перегиба.
— точка перегиба.
б)
График функции
![]() выпуклый при
выпуклый при![]() ,
вогнутый при
,
вогнутый при![]() ;
;![]() — точки перегиба.
— точки перегиба.
в)
График функции
![]() выпуклый при
выпуклый при![]() ,
вогнутый при
,
вогнутый при![]() ;
;![]() — точка перегиба.
— точка перегиба.
3)
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Занятие №12
Общая схема исследования функций и построения их графиков
Исследование функций и построение их графиков следует проводить по следующему плану:
Найти область определения функции; указать точки разрыва;
Определить чётность (нечётность), периодичность функции;
Найти интервалы возрастания (убывания) функции и её экстремумы;
Найти интервалы выпуклости (вогнутости) и точки перегиба графика функции;
Найти асимптоты графика функции;
Найти точки пересечения графика с осями координат;
Построить график по результатам этого исследования.
Примеры
Исследовать функцию
 и
построить её график.
и
построить её график.
1)
Область определения функции:
![]() ;
;![]() — точка разрыва 2-го рода;
— точка разрыва 2-го рода;
2)
функция не является ни чётной, ни нечётной
(так как не выполняются равенства
![]() для всех
для всех![]() из области определения функции); функция
не является периодической;
из области определения функции); функция
не является периодической;
3)
найдём
![]() .
.
Имеем:
![]() при
при![]() ;
;![]() при
при![]() .
Получаем следующее распределение знаков
.
Получаем следующее распределение знаков![]() ,
по которому мы определяем, на каких
интервалах функция
,
по которому мы определяем, на каких
интервалах функция![]() возрастает, а на каких — убывает:
возрастает, а на каких — убывает:
-
x



0

y'
—
0
+
∞
—
y

Точка минимума

Точка разрыва

Так
как знак
![]() при переходе через точку
при переходе через точку![]() изменяется с «—» на «+», то в этой точке
у функции минимум, причём
изменяется с «—» на «+», то в этой точке
у функции минимум, причём ;
;
Найдём
 .
Очевидно, что
.
Очевидно, что при
при .
Поэтому точек перегиба нет, а график
функции вогнутый всюду;
.
Поэтому точек перегиба нет, а график
функции вогнутый всюду;
-
x

0

y'’
+
∞
+
y

Точка раз-рыва

5)
Найдём асимптоты графика. Прямая
![]() — вертикальная асимптота, так как
— вертикальная асимптота, так как![]() — точка разрыва 2-го рода. Ищем наклонные
асимптоты вида
— точка разрыва 2-го рода. Ищем наклонные
асимптоты вида![]() .
Имеем:
.
Имеем:
![]() ;
;
![]() .
Поэтому
.
Поэтому![]() — наклонная асимптота при
— наклонная асимптота при![]() .
.
6)
Найдём точки пересечения графика с
осями координат. Для этого в общем случае
надо взять
![]() и найти соответствующее значение
и найти соответствующее значение![]() .
Затем взять
.
Затем взять![]() и найти соответствующее значение
и найти соответствующее значение![]() .
В данном случае получаем только одну
такую точку:
.
В данном случае получаем только одну
такую точку:![]() .
.
7) Построить график функции по результатам этого исследования. Для этого сначала строим асимптоты (если они есть), и указываем опорные точки: экстремумы, точки перегиба, точки пересечения с осями координат.




![]()
![]()

![]()

 1
1
![]()
![]()
![]()
Рис. 2
Замечание.
График функции асимптоту не пересекает,
так как уравнение
![]() не имеет решений.
не имеет решений.
Исследовать функцию
 и построить её график.
и построить её график.
1) Область определения функции:
 ;
; — точки разрыва.2-го рода;
— точки разрыва.2-го рода;
Функция нечётная, т.е.
 ;
функция не является периодической.
;
функция не является периодической.Найдём
 .
Имеем:
.
Имеем: при
при ;
;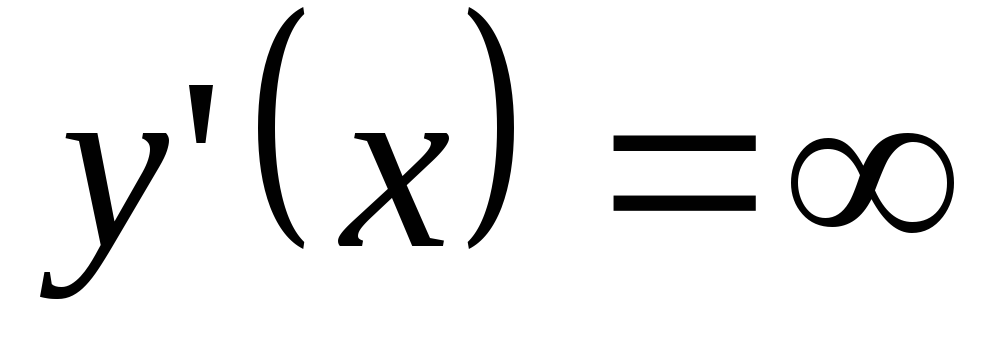 при
при .
Получаем следующее распределение
знаков
.
Получаем следующее распределение
знаков ,
по которому мы определяем, на каких
интервалах функция
,
по которому мы определяем, на каких
интервалах функция возрастает, а на каких — убывает.
возрастает, а на каких — убывает.
|
x |
|
|
|
|
|
0 |
|
|
|
3 |
|
|
y' |
— |
0 |
+ |
∞ |
+ |
0 |
+ |
∞ |
+ |
0 |
— |
|
|
|
Т.мин. |
|
Точка разр. |
|
0 |
|
Т. разр. |
|
Т. макс. |
|
Так
как знак
![]() при переходе аргумента
при переходе аргумента![]() через точки
через точки![]() меняется, то в этих точках — экстремумы,
причём
меняется, то в этих точках — экстремумы,
причём![]() ,
,![]() .
.
Найдём
 .
Очевидно, что
.
Очевидно, что при
при ;
; при
при .
Получаем следующую расстановку знаков
.
Получаем следующую расстановку знаков ,
по которой мы определяем, на каких
интервалах график функции
,
по которой мы определяем, на каких
интервалах график функции выпуклый, а на каких — вогнутый.
выпуклый, а на каких — вогнутый.
-
x



0



y'’
+
∞
—
0
+
∞
—


y
Т.раз-рыва.

Т. пере-гиба
Т.раз-рыва

5)
Найдём асимпоты графика. Прямые
![]() — вертикальные асимптоты, так как
— вертикальные асимптоты, так как![]() — точки разрыва 2-го рода. Ищем наклонные
асимптоты вида
— точки разрыва 2-го рода. Ищем наклонные
асимптоты вида![]() .
Имеем:
.
Имеем:
![]() ;
;
![]() .
Поэтому
.
Поэтому![]() — наклонная асимптота при
— наклонная асимптота при![]() .
.
6)
Найдём точки пересечения графика с
осями координат. В данном случае получаем
только одну такую точку
![]() .
.
7) Построим график по результатам этого исследования:
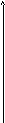





![]()
![]()



![]()
![]()
![]()

-3
![]() 3
3

Рис. 3


 y
y


